Question:
(a) Show that if P satisfies the logistic equation (4), then
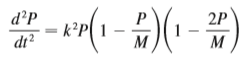
(b) Deduce that a population grows fastest when it reaches half its carrying capacity.
Transcribed Image Text:
d²P P 2P k²P dt? M M
> Find the radius of convergence and interval of convergence of the series. n?x" Σ 2.4.6. .... (2n) n-1
> In formulated a model for learning in the form of the differential equation where P(t) measures the performance of someone learning a skill after a training time t, M is the maximum level of performance, and k is a positive constant. Solve this different
> In Exercise 9.2.28 we discussed a differential equation that models the temperature of a 95°C cup of coffee in a 20°C room. Solve the differential equation to find an expression for the temperature of the coffee at time t. Data from Exercise 9.2.28: In
> Solve the initial-value problem in Exercise 9.2.27 to find an expression for the charge at time t. Find the limiting value of the charge. Data from Exercise 9.2.27: The figure shows a circuit containing an electromotive force, a capacitor with a capaci
> Find a function f such that f(3) = 2 and (1? + 1)f"(1) + [f(1)]² + 1 = 0 t#1 ||
> An integral equation is an equation that contains an unknown function y(x) and an integral that involves y(x). Solve the given integral equation. y(x) у() — 4 + ("2у) 21/y(1) dt
> An integral equation is an equation that contains an unknown function y(x) and an integral that involves y(x). Solve the given integral equation. dt Уб) — 2 + ( ry(1) y(x) x>0
> An integral equation is an equation that contains an unknown function y(x) and an integral that involves y(x). Solve the given integral equation. y(x) [t - ty(1)] dt
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. 1 y = x + k
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. y
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. y? = kx' .3
> Find the radius of convergence and interval of convergence of the series. E n!(2x – 1)"
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. x² + 2y? = k?
> (a) Use a computer algebra system to draw a direction field for the differential equation. Get a printout and use it to sketch some solution curves without solving the differential equation. (b) Solve the differential equation. (c) Use the CAS to draw se
> (a) Use a computer algebra system to draw a direction field for the differential equation. Get a printout and use it to sketch some solution curves without solving the differential equation. (b) Solve the differential equation. (c) Use the CAS to draw se
> Solve the differential equation y’ = x + y by making the change of variable u = x + y.
> Find the function f such that f’(x) = xf(x) – x and f(0) = 2.
> Find the radius of convergence and interval of convergence of the series. b" Σ -(х — а)", Ь>0 In n n-2
> Find an equation of the curve that passes through the point s0, 2d and whose slope at (x, y) is x/y.
> Find the solution of the differential equation that satisfies the given initial condition. dL kL² In t, L(1) = -1 dt
> Find the solution of the differential equation that satisfies the given initial condition. у' tan x — а + у, у(п/3) — а, 0<x<п/2
> Find the solution of the differential equation that satisfies the given initial condition. dP Pt , dt Р(1) — 2
> Find the solution of the differential equation that satisfies the given initial condition. x In x = y(1 + /3 + y² ) y', y(1) = 1
> Find the solution of the differential equation that satisfies the given initial condition. dy x + 3y' /x? + T = 0, y(0) = 1 dx
> Find the solution of the differential equation that satisfies the given initial condition. du 21 + sec?t u(0) = -5 %3D dt 2u
> Find the solution of the differential equation that satisfies the given initial condition. dy x sin x y(0) dx y
> Find the solution of the differential equation that satisfies the given initial condition. dy - хе', у(0) — 0 dx
> Solve the differential equation. dz + ettz = 0 dt
> Find the radius of convergence and interval of convergence of the series. - (х — а)", Ь> 0 Σ b" n-1
> Solve the differential equation. dp uP. = t°p – p + t² – 1 dt
> Solve the differential equation. dH_ /T + R² In H RH² dR
> Solve the differential equation. de t sec 0 dt Oe“
> Solve the differential equation. du 1+ t4 dt ut? + u*1?
> Solve the differential equation. (e – 1)y' = 2 + cosx
> Solve the differential equation. y' + xe' = 0 хе
> Solve the differential equation. хуу' — х? + 1
> Solve the differential equation. dy x- dx
> Solve the differential equation. dy 3x²y? dx %3D
> Graphs of logistic functions look suspiciously similar to the graph of the hyperbolic tangent function Explain the similarity by showing that the logistic function given by Equation 7 can be written as where c = (ln A)/k. Thus the logistic function is re
> Find the radius of convergence and interval of convergence of the series. (2х — 1)" Σ 5"/n
> Another model for a growth function for a limited population is given by the Gompertz function, which is a solution of the differential equation where c is a constant and M is the carrying capacity. (a) Solve this differential equation. (b) Compute / (c)
> There is considerable evidence to support the theory that for some species there is a minimum population m such that the species will become extinct if the size of the population falls below m. This condition can be incorporated into the logistic equatio
> Consider the differential equation as a model for a fish population, where t is measured in weeks and c is a constant. (a) Use a CAS to draw direction fields for various values of c. (b) From your direction fields in part (a), determine the values of c f
> Let’s modify the logistic differential equation of Example 1 as follows: (a) Suppose P(t) represents a fish population at time t, where t is measured in weeks. Explain the meaning of the final term in the equation s215d. (b) Draw a dire
> Let c be a positive number. A differential equation of the form where k is a positive constant, is called a doomsday equation because the exponent in the expression ky11c is larger than the exponent 1 for natural growth. (a) Determine the solution that s
> The table gives the midyear population of Norway, in thousands, from 1960 to 2010. Use a calculator to fit both an exponential function and a logistic function to these data. Graph the data points and both functions, and comment on the accuracy of the
> The table gives the midyear population of Japan, in thousands, from 1960 to 2010. Use a calculator to fit both an exponential function and a logistic function to these data. Graph the data points and both functions, and comment on the accuracy of the m
> Find the radius of convergence and interval of convergence of the series. (x – 2)" Σ 一1 n"
> For a fixed value of M (say M − 10), the family of logistic functions given by Equation 7 depends on the initial value P0 and the proportionality constant k. Graph several members of this family. How does the graph change when P0 varies? How does it chan
> Biologists stocked a lake with 400 fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be 10,000. The number of fish tripled in the first year. (a) Assuming that the size of the fish population s
> One model for the spread of a rumor is that the rate of spread is proportional to the product of the fraction y of the population who have heard the rumor and the fraction who have not heard the rumor. (a) Write a differential equation that is satisfied
> (a) Assume that the carrying capacity for the US population is 800 million. Use it and the fact that the population was 282 million in 2000 to formulate a logistic model for the US population. (b) Determine the value of k in your model by using the fact
> The population of the world was about 6.1 billion in 2000. Birth rates around that time ranged from 35 to 40 million per year and death rates ranged from 15 to 20 million per year. Let’s assume that the carrying capacity for world population is 20 billio
> The table gives the number of yeast cells in a new laboratory culture. (a) Plot the data and use the plot to estimate the carrying capacity for the yeast population. (b) Use the data to estimate the initial relative growth rate. (c) Find both an expone
> Suppose a population grows according to a logistic model with initial population 1000 and carrying capacity 10,000. If the population grows to 2500 after one year, what will the population be after another three years?
> Suppose a population P(t) satisfies where t is measured in years. (a) What is the carrying capacity? (b) What is P(0)? (c) When will the population reach 50% of the carrying capacity? dP 0.4P – 0.001P²2 dt P(0) = 50
> The Pacific halibut fishery has been modeled by the differential equation where y(t) is the biomass (the total mass of the members of the population) in kilograms at time t (measured in years), the carrying capacity is estimated to be M âˆ&#
> Find the radius of convergence and interval of convergence of the series. (r+ 6)" 一1 ー 84
> Suppose that a population grows according to a logistic model with carrying capacity 6000 and k = 0.0015 per year. (a) Write the logistic differential equation for these data. (b) Draw a direction field (either by hand or with a computer algebra system)
> Suppose that a population develops according to the logistic equation where t is measured in weeks. (a) What is the carrying capacity? What is the value of k? (b) A direction field for this equation is shown. Where are the slopes close to 0? Where are th
> A population grows according to the given logistic equation, where t is measured in weeks. (a) What is the carrying capacity? What is the value of k? (b) Write the solution of the equation. (c) What is the population after 10 weeks? dP 0.02P – 0.0004
> A population grows according to the given logistic equation, where t is measured in weeks. (a) What is the carrying capacity? What is the value of k? (b) Write the solution of the equation. (c) What is the population after 10 weeks? dP P 0.04P( 1 dt
> To account for seasonal variation in the logistic differential equation, we could allow k and M to be functions of t: (a) Verify that the substitution z = 1/P transforms this equation into the linear equation (b) Write an expression for the solution of t
> (a) Show that the substitution z = 1/P transforms the logistic differential equation P = kP (1 - P/M) into the linear differential equation (b) Solve the linear differential equation in part (a) and thus obtain an expression for P(t). Compare with Equati
> If we ignore air resistance, we can conclude that heavier objects fall no faster than lighter objects. But if we take air resistance into account, our conclusion changes. Use the expression for the velocity of a falling object in Exercise 35(a) to find d
> An object with mass m is dropped from rest and we assume that the air resistance is proportional to the speed of the object. If s(t) is the distance dropped after t seconds, then the speed is v = s(t) and the acceleration is a = v(t). If t is the acceler
> A tank with a capacity of 400 L is full of a mixture of water and chlorine with a concentration of 0.05 g of chlorine per liter. In order to reduce the concentration of chlorine, fresh water is pumped into the tank at a rate of 4 L/s. The mixture is kept
> In Section 9.3 we looked at mixing problems in which the volume of fluid remained constant and saw that such problems give rise to separable differentiable equations. (See Example 6 in that section.) If the rates of flow into and out of the system are di
> Find the radius of convergence and interval of convergence of the series. (x + 2)" Σ n-2 2" In n
> Two new workers were hired for an assembly line. Jim processed 25 units during the first hour and 45 units during the second hour. Mark processed 35 units during the first hour and 50 units the second hour. Using the model of Exercise 31 and assuming tha
> Let P(t) be the performance level of someone learning a skill as a function of the training time t. The graph of P is called a learning curve. In Exercise 9.1.15 we proposed the differential equation as a reasonable model for learning, where
> In the circuit of Exercise 29, R = 2 V, C − 0.01 F, Q(0) = 0, and E(t) = 10sin 60t. Find the charge and the current at time t. Data from Exercise 29: The figure shows a circuit containing an electromotive force, a capacitor with a cap
> The figure shows a circuit containing an electromotive force, a capacitor with a capacitance of C farads (F), and a resistor with a resistance of R ohms (V). The voltage drop across the capacitor is Q/C, where Q is the charge (in coulombs), so in this ca
> In the circuit shown in Figure 4, a generator supplies a voltage of E(t) = 40 sin 50t volts the inductance is 1 H, the resistance is 20 V, and I(0) = 1 A. (a) Find I(t). (b) Find the current after 0.1 seconds. (c) Use a graphing device to draw the graph
> In the circuit, a battery supplies a constant voltage of 40 V, the inductance is 2 H, the resistance is 10 V, and I(0) = 0. (a) Find I(t). (b) Find the current after 0.1 seconds.
> Solve the second-order equation xyn + 2y’ = 12x2 by making the substitution /
> Use the method of Exercise 23 to solve the differential equation. Data from Exercise 23: A Bernoulli differential equation (named after James Bernoulli) is of the form Observe that, if n = 0 or 1, the Bernoulli equation is linear. For other values of
> Use the method of Exercise 23 to solve the differential equation. Data from Exercise 23: A Bernoulli differential equation (named after James Bernoulli) is of the form Observe that, if n = 0 or 1, the Bernoulli equation is linear. For other values of
> A Bernoulli differential equation (named after James Bernoulli) is of the form Observe that, if n = 0 or 1, the Bernoulli equation is linear. For other values of n, show that the substitution u = y1-n transforms the Bernoulli equation into the linear eq
> Find the radius of convergence and interval of convergence of the series. (-1)" Σ (2n – 1)2" - (x – 1)" n-1
> Solve the differential equation and use a calculator to graph several members of the family of solutions. How does the solution curve change as C varies? ху' — xy' х3 + 2у
> Solve the differential equation and use a calculator to graph several members of the family of solutions. How does the solution curve change as C varies? ху' + 2у— е*
> Solve the initial-value problem. dy + 3x(у — 1) — о, у(0) — 2 dx %3D (x² + 1)
> Solve the initial-value problem. ху' — у + x* sin x, у(п) — 0
> Solve the initial-value problem. ху' + у — x Iп х, у(1) — 0
> Solve the initial-value problem. du — ? + Зи, 1> 0, и(2) — 4 dt
> Solve the initial-value problem. dy + 31'у — сos t, У(т) — 0 dt
> Solve the initial-value problem. x'у + 2ху — In x, у(1) — 2
> Solve the differential equation. dr t In t +r = te' dt
> Solve the differential equation. dy 12 + 3ty = vI + 1², t>0 dt V1 + 1² t > 0
> Find the radius of convergence and interval of convergence of the series. (х — 2)" .2 + 1 n-o n° + 1
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Solve the differential equation. у + 2ху — 1
> Solve the differential equation. ху x>0
> Solve the differential equation. 2ху' + у — 2
> Solve the differential equation. xy' + y = Vx
> Solve the differential equation. 4x'y + x*y' = sin'x
> Solve the differential equation. y' = x - y
> Solve the differential equation. y' - y = e*
> Solve the differential equation. y' + y = 1

