Question: Find the orthogonal trajectories of the family
Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen.
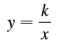
Transcribed Image Text:
y
> Use Euler’s method with step size 0.1 to estimate ys0.5d, where y(x) is the solution of the initial-value problem /
> Use Euler’s method with step size 0.2 to estimate ys1d, where y(x) is the solution of the initial-value problem /
> Use Euler’s method with step size 0.5 to compute the approximate y-values y1, y2, y3, and y4 of the solution of the initial-value problem /
> A direction field for a differential equation is shown. Draw, with a ruler, the graphs of the Euler approximations to the solution curve that passes through the origin. Use step sizes h = 1 and h = 0.5. Will the Euler estimates be underestimates or overe
> (a) Use Euler’s method with each of the following step sizes to estimate the value of y(0.4), where y is the solution of the initial-value problem / / (b) We know that the exact solution of the initial-value problem in part (a) is y − ex. Draw, as accur
> Make a rough sketch of a direction field for the autonomous differential equation / where the graph off is as shown. How does the limiting behavior of solutions depend on the value of y(0)? y' = f(y).
> Use a computer algebra system to draw a direction field for the differential equation / Get a printout and sketch on it solutions that satisfy the initial condition y(0) = c for various values of c. For what values of c does / What are the possible value
> Use a computer algebra system to draw a direction field for the given differential equation. Get a printout and sketch on it the solution curve that passes through (0, 1). Then use the CAS to draw the solution curve and compare it with your sketch. y
> Find the radius of convergence and interval of convergence of the series. x" Σ 1 1 · 3 · 5 · .. 1:3. 5. ... · (2n – 1)
> Use a computer algebra system to draw a direction field for the given differential equation. Get a printout and sketch on it the solution curve that passes through (0, 1). Then use the CAS to draw the solution curve and compare it with your sketch. y
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point y' - x + y', (0, 0)
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point. у' — у+ ху, (0, 1)
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point. У — ху — х, (0, 1)
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point. у — у — 2х, (1, 0)
> Sketch a direction field for the differential equation. Then use it to sketch three solution curves. - y' = x - y + 1
> Sketch a direction field for the differential equation. Then use it to sketch three solution curves. y' = ły
> Use the direction field labeled III (above) to sketch the graphs of the solutions that satisfy the given initial conditions. (b) у(0) — 2.5 (с) у(0) — 3.5 %3D (а) у(0) — 1 %3D %3D
> Use the direction field labeled I (above) to sketch the graphs of the solutions that satisfy the given initial conditions. (а) у(0) — 1 () у(0) — 2.5 (с) у(0) — 3.5
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = sin x sin y yA IV -- -- -
> Find the radius of convergence and interval of convergence of the series. Σ n(In n)² n-2
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = x + y – 1 III -2 حر ر
> (a) For what values of k does the function y = cos k t satisfy the differential equation / (b) For those values of k, verify that every member of the family of functions y = A sin k t + B cos k t is also a solution.
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = 2 - y yA I --- %3D -- 2 * // 2.
> According to Newton’s Law of Universal Gravitation, the gravitational force on an object of mass m that has been projected vertically upward from the earth’s surface is where x = x(t) is the object’s
> Let A(t) be the area of a tissue culture at time t and let M be the final area of the tissue when growth is complete. Most cell divisions occur on the periphery of the tissue and the number of cells on the periphery is proportional to / So a reasonable m
> A model for tumor growth is given by the Gompertz equation where a and b are positive constants and V is the volume of the tumor measured in mm3. (a) Find a family of solutions for tumor volume as a function of time. (b) Find the solution that has an ini
> Allometric growth in biology refers to relationships between sizes of parts of an organism (skull length and body length, for instance). If L1(t) and L2(t) are the sizes of two organs in an organism of age t, then L1 and L2 satisfy an allometric law if t
> An object of mass m is moving horizontally through a medium which resists the motion with a force that is a function of the velocity; that is, where v = v(t) and s = s(t) represent the velocity and position of the object at time t, respectively. For exam
> Find the radius of convergence and interval of convergence of the series. (5х — 4)" Σ R-1
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> When a raindrop falls, it increases in size and so its mass at time t is a function of t, namely, m(t). The rate of growth of the mass is km(t) for some positive constant k. When we apply New ton’s Law of Motion to the raindrop, we get (mv) = tm, where v
> A tank contains 1000 L of pure water. Brine that contains 0.05 kg of salt per liter of water enters the tank at a rate of 5 L/min. Brine that contains 0.04 kg of salt per liter of water enters the tank at a rate of 10 L/min. The solution is kept thorough
> A vat with 500 gallons of beer contains 4% alcohol (by volume). Beer with 6% alcohol is pumped into the vat at a rate of 5 gal/min and the mixture is pumped out at the same rate. What is the percentage of alcohol after an hour?
> The air in a room with volume 180 m3 contains 0.15% carbon dioxide initially. Fresher air with only 0.05% carbon dioxide flows into the room at a rate of 2 m3ymin and the mixed air flows out at the same rate. Find the percentage of carbon dioxide in the
> A tank contains 1000 L of brine with 15 kg of dissolved salt. Pure water enters the tank at a rate of 10 L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank (a) after t minutes and (b) afte
> A certain small country has $10 billion in paper currency in circulation, and each day $50 million comes into the country’s banks. The government decides to introduce new currency by having the banks replace old bills with new ones whenever old currency
> A glucose solution is administered intravenously into the bloodstream at a constant rate r. As the glucose is added, it is converted into other substances and removed from the bloodstream at a rate that is proportional to the concentration at
> A sphere with radius 1 m has temperature 15 8C. It lies inside a concentric sphere with radius 2 m and temperature 25 8C. The temperature T(rd) at a distance r from the common center of the spheres satisfies the differential equation If we let S = dT/dr,
> In contrast to the situation of Exercise 40, experiments show that the reaction / satisfies the rate law and so for this reaction the differential equation becomes where x = [HBr] and a and b are the initial concentrations of hydrogen and bromine. (a) Fi
> In an elementary chemical reaction, single molecules of two reactants A and B form a molecule of the product C: A + B → C. The law of mass action states that the rate of reaction is proportional to the product of the concentrations of A
> Find the radius of convergence and interval of convergence of the series. n?x" Σ 2.4.6. .... (2n) n-1
> In formulated a model for learning in the form of the differential equation where P(t) measures the performance of someone learning a skill after a training time t, M is the maximum level of performance, and k is a positive constant. Solve this different
> In Exercise 9.2.28 we discussed a differential equation that models the temperature of a 95°C cup of coffee in a 20°C room. Solve the differential equation to find an expression for the temperature of the coffee at time t. Data from Exercise 9.2.28: In
> Solve the initial-value problem in Exercise 9.2.27 to find an expression for the charge at time t. Find the limiting value of the charge. Data from Exercise 9.2.27: The figure shows a circuit containing an electromotive force, a capacitor with a capaci
> Find a function f such that f(3) = 2 and (1? + 1)f"(1) + [f(1)]² + 1 = 0 t#1 ||
> An integral equation is an equation that contains an unknown function y(x) and an integral that involves y(x). Solve the given integral equation. y(x) у() — 4 + ("2у) 21/y(1) dt
> An integral equation is an equation that contains an unknown function y(x) and an integral that involves y(x). Solve the given integral equation. dt Уб) — 2 + ( ry(1) y(x) x>0
> An integral equation is an equation that contains an unknown function y(x) and an integral that involves y(x). Solve the given integral equation. y(x) [t - ty(1)] dt
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. 1 y = x + k
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. y? = kx' .3
> Find the radius of convergence and interval of convergence of the series. E n!(2x – 1)"
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. x² + 2y? = k?
> (a) Use a computer algebra system to draw a direction field for the differential equation. Get a printout and use it to sketch some solution curves without solving the differential equation. (b) Solve the differential equation. (c) Use the CAS to draw se
> (a) Use a computer algebra system to draw a direction field for the differential equation. Get a printout and use it to sketch some solution curves without solving the differential equation. (b) Solve the differential equation. (c) Use the CAS to draw se
> Solve the differential equation y’ = x + y by making the change of variable u = x + y.
> Find the function f such that f’(x) = xf(x) – x and f(0) = 2.
> Find the radius of convergence and interval of convergence of the series. b" Σ -(х — а)", Ь>0 In n n-2
> Find an equation of the curve that passes through the point s0, 2d and whose slope at (x, y) is x/y.
> Find the solution of the differential equation that satisfies the given initial condition. dL kL² In t, L(1) = -1 dt
> Find the solution of the differential equation that satisfies the given initial condition. у' tan x — а + у, у(п/3) — а, 0<x<п/2
> Find the solution of the differential equation that satisfies the given initial condition. dP Pt , dt Р(1) — 2
> Find the solution of the differential equation that satisfies the given initial condition. x In x = y(1 + /3 + y² ) y', y(1) = 1
> Find the solution of the differential equation that satisfies the given initial condition. dy x + 3y' /x? + T = 0, y(0) = 1 dx
> Find the solution of the differential equation that satisfies the given initial condition. du 21 + sec?t u(0) = -5 %3D dt 2u
> Find the solution of the differential equation that satisfies the given initial condition. dy x sin x y(0) dx y
> Find the solution of the differential equation that satisfies the given initial condition. dy - хе', у(0) — 0 dx
> Solve the differential equation. dz + ettz = 0 dt
> Find the radius of convergence and interval of convergence of the series. - (х — а)", Ь> 0 Σ b" n-1
> Solve the differential equation. dp uP. = t°p – p + t² – 1 dt
> Solve the differential equation. dH_ /T + R² In H RH² dR
> Solve the differential equation. de t sec 0 dt Oe“
> Solve the differential equation. du 1+ t4 dt ut? + u*1?
> Solve the differential equation. (e – 1)y' = 2 + cosx
> Solve the differential equation. y' + xe' = 0 хе
> Solve the differential equation. хуу' — х? + 1
> Solve the differential equation. dy x- dx
> Solve the differential equation. dy 3x²y? dx %3D
> Graphs of logistic functions look suspiciously similar to the graph of the hyperbolic tangent function Explain the similarity by showing that the logistic function given by Equation 7 can be written as where c = (ln A)/k. Thus the logistic function is re
> Find the radius of convergence and interval of convergence of the series. (2х — 1)" Σ 5"/n
> Another model for a growth function for a limited population is given by the Gompertz function, which is a solution of the differential equation where c is a constant and M is the carrying capacity. (a) Solve this differential equation. (b) Compute / (c)
> There is considerable evidence to support the theory that for some species there is a minimum population m such that the species will become extinct if the size of the population falls below m. This condition can be incorporated into the logistic equatio
> Consider the differential equation as a model for a fish population, where t is measured in weeks and c is a constant. (a) Use a CAS to draw direction fields for various values of c. (b) From your direction fields in part (a), determine the values of c f
> Let’s modify the logistic differential equation of Example 1 as follows: (a) Suppose P(t) represents a fish population at time t, where t is measured in weeks. Explain the meaning of the final term in the equation s215d. (b) Draw a dire
> Let c be a positive number. A differential equation of the form where k is a positive constant, is called a doomsday equation because the exponent in the expression ky11c is larger than the exponent 1 for natural growth. (a) Determine the solution that s
> The table gives the midyear population of Norway, in thousands, from 1960 to 2010. Use a calculator to fit both an exponential function and a logistic function to these data. Graph the data points and both functions, and comment on the accuracy of the
> The table gives the midyear population of Japan, in thousands, from 1960 to 2010. Use a calculator to fit both an exponential function and a logistic function to these data. Graph the data points and both functions, and comment on the accuracy of the m
> Find the radius of convergence and interval of convergence of the series. (x – 2)" Σ 一1 n"
> For a fixed value of M (say M − 10), the family of logistic functions given by Equation 7 depends on the initial value P0 and the proportionality constant k. Graph several members of this family. How does the graph change when P0 varies? How does it chan
> (a) Show that if P satisfies the logistic equation (4), then (b) Deduce that a population grows fastest when it reaches half its carrying capacity. d²P P 2P k²P dt? M M
> Biologists stocked a lake with 400 fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be 10,000. The number of fish tripled in the first year. (a) Assuming that the size of the fish population s
> One model for the spread of a rumor is that the rate of spread is proportional to the product of the fraction y of the population who have heard the rumor and the fraction who have not heard the rumor. (a) Write a differential equation that is satisfied
> (a) Assume that the carrying capacity for the US population is 800 million. Use it and the fact that the population was 282 million in 2000 to formulate a logistic model for the US population. (b) Determine the value of k in your model by using the fact
> The population of the world was about 6.1 billion in 2000. Birth rates around that time ranged from 35 to 40 million per year and death rates ranged from 15 to 20 million per year. Let’s assume that the carrying capacity for world population is 20 billio
> The table gives the number of yeast cells in a new laboratory culture. (a) Plot the data and use the plot to estimate the carrying capacity for the yeast population. (b) Use the data to estimate the initial relative growth rate. (c) Find both an expone
> Suppose a population grows according to a logistic model with initial population 1000 and carrying capacity 10,000. If the population grows to 2500 after one year, what will the population be after another three years?
> Suppose a population P(t) satisfies where t is measured in years. (a) What is the carrying capacity? (b) What is P(0)? (c) When will the population reach 50% of the carrying capacity? dP 0.4P – 0.001P²2 dt P(0) = 50
> The Pacific halibut fishery has been modeled by the differential equation where y(t) is the biomass (the total mass of the members of the population) in kilograms at time t (measured in years), the carrying capacity is estimated to be M âˆ&#
> Find the radius of convergence and interval of convergence of the series. (r+ 6)" 一1 ー 84
> Suppose that a population grows according to a logistic model with carrying capacity 6000 and k = 0.0015 per year. (a) Write the logistic differential equation for these data. (b) Draw a direction field (either by hand or with a computer algebra system)
> Suppose that a population develops according to the logistic equation where t is measured in weeks. (a) What is the carrying capacity? What is the value of k? (b) A direction field for this equation is shown. Where are the slopes close to 0? Where are th

