Question: Match the differential equation with its direction
Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer.
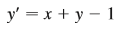
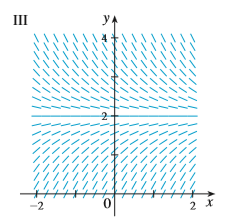
Transcribed Image Text:
y' = x + y – 1 III -2 حر ر
> An online retailer has determined that the average time for credit card transactions to be electronically approved is 1.6 seconds. (a) Use an exponential density function to find the probability that a customer waits less than a second for credit card ap
> Show that the median waiting time for a phone call to the company described in Example 4 is about 3.5 minutes.
> (a) Explain why the function whose graph is shown is a probability density function. (b) Use the graph to find the following probabilities: (i) P(X (ii) P(3 (c) Calculate the mean. y. 0.2 y= f(x) 0.1 2 4 8 10
> A spinner from a board game randomly indicates a real number between 0 and 10. The spinner is fair in the sense that it indicates a number in a given interval with the same probability as it indicates a number in any other interval of the same length. (a
> Let f(x) = k (3x – x2) if 0 ≤ x ≤ 3 and f(x) = 0 if x 3. (a) For what value of k is f a probability density function? (b) For that value of k, find P(X > 1). (c) Find the mean.
> Let f(x) = c/(1 = x2). (a) For what value of c is f a probability density function? (b) For that value of c, find P(21 , X , 1).
> The density function is an example of a logistic distribution. (a) Verify that f is a probability density function. (b) Find P(3 (c) Graph f. What does the mean appear to be? What about the median? e3-1 f(x) (1 + e³ =)²
> Let f(x) = 30x2 (1 – x)2 for 0 ≤ x ≤ 1 and f(x) − 0 for all other values of x. (a) Verify that f is a probability density function. (b) Find P(X <).
> Let f(t) be the probability density function for the time it takes you to drive to school in the morning, where t is measured in minutes. Express the following probabilities as integrals. (a) The probability that you drive to school in less than 15 minut
> Let f(x) be the probability density function for the lifetime of a manufacturer’s highest quality car tire, where x is measured in miles. Explain the meaning of each integral. r40,000 (а) У30,000 f(x) dx (b) 25,000 km f(x) dx my
> Von Bertalanffy’s equation states that the rate of growth in length of an individual fish is proportional to the difference between the current length L and the asymptotic length L` (in centimeters). (a) Write a differential equation that expresses this
> Psychologists interested in learning theory study learning curves. A learning curve is the graph of a function P(t), the performance of someone learning a skill as a function of the training time t. The derivative dP/dt represents the rate at which perfo
> Suppose you have just poured a cup of freshly brewed coffee with temperature 95°C in a room where the temperature is 20°C. (a) When do you think the coffee cools most quickly? What happens to the rate of cooling as time goes by? Explain. (b) Newton’s Law
> Match the differential equations with the solution graphs labeled I–IV. Give reasons for your choices. (a) y' = 1 + x? + y² (b) у' — хе * y? 1 (c) y' (d) y' = sin(xy) cos(xy) 1 + e*²+y" I II III IV yA
> The function with the given graph is a solution of one of the following differential equations. Decide which is the correct equation and justify your answer. А. у'— 1 + ху B. y' = -2xy С. у'— 1 - 2ху
> Explain why the functions with the given graphs can’t be solutions of the differential equation dy e'(y – 1)? dt (а) Уд (b) У 1
> The Fitzhugh-Nagumo model for the electrical impulse in a neuron states that, in the absence of relaxation effects, the electrical potential in a neuron v(t) obeys the differential equation where a is a positive constant such that 0 (a) For what values o
> A population is modeled by the differential equation (a) For what values of P is the population increasing? (b) For what values of P is the population decreasing? (c) What are the equilibrium solutions? dP P 1.2P dt 4200
> (a) What can you say about the graph of a solution of the equation / when x is close to 0? What if x is large? (b) Verify that all members of the family / are solutions of the differential equation / (c) Graph several members of the family of solutions
> (a) What can you say about a solution of the equation y’ = -y2 just by looking at the differential equation? (b) Verify that all members of the family /are solutions of the equation in part (a). (c) Can you think of a solution of the di
> (a) Show that every member of the family of functions y = (In x + C)/x is a solution of the differential equation / (b) Illustrate part (a) by graphing several members of the family of solutions on a common screen. (c) Find a solution of the differential
> Which of the following functions are solutions of the differential equation / у" + у— sin x? SI
> Verify that y = -t cos t = t is a solution of the initial value problem dy =y + t°sin t y(7) = 0 dt
> In Exercise 9.1.14 we considered a 958C cup of coffee in a 208C room. Suppose it is known that the coffee cools at a rate of 18C per minute when its temperature is 70°C. (a) What does the differential equation become in this case? (b) Sketch a direction
> The figure shows a circuit containing an electromotive force, a capacitor with a capacitance of C farads (F), and a resistor with a resistance of R ohms (V). The voltage drop across the capacitor is Q/C, where Q is the charge (in coulombs, C), so in this
> (a) Program your computer algebra system, using Euler’s method with step size 0.01, to calculate ys2d, where y is the solution of the initial-value problem (b) Check your work by using the CAS to draw the solution curve. y' = x' -
> Find the radius of convergence and interval of convergence of the series. n!x" Σ 1.3· 5. .... (2n – 1)
> (a) Program a calculator or computer to use Euler’s method to compute ys1d, where y(x) is the solution of the initial value problem (b) Verify that y = 2 + e2x3 is the exact solution of the differential equation. (c) Find the errors in
> (a) Use Euler’s method with step size 0.2 to estimate ys0.6d, where y(x) is the solution of the initial-value problem / (b) Repeat part (a) with step size 0.1.
> Use Euler’s method with step size 0.1 to estimate ys0.5d, where y(x) is the solution of the initial-value problem /
> Use Euler’s method with step size 0.2 to estimate ys1d, where y(x) is the solution of the initial-value problem /
> Use Euler’s method with step size 0.5 to compute the approximate y-values y1, y2, y3, and y4 of the solution of the initial-value problem /
> A direction field for a differential equation is shown. Draw, with a ruler, the graphs of the Euler approximations to the solution curve that passes through the origin. Use step sizes h = 1 and h = 0.5. Will the Euler estimates be underestimates or overe
> (a) Use Euler’s method with each of the following step sizes to estimate the value of y(0.4), where y is the solution of the initial-value problem / / (b) We know that the exact solution of the initial-value problem in part (a) is y − ex. Draw, as accur
> Make a rough sketch of a direction field for the autonomous differential equation / where the graph off is as shown. How does the limiting behavior of solutions depend on the value of y(0)? y' = f(y).
> Use a computer algebra system to draw a direction field for the differential equation / Get a printout and sketch on it solutions that satisfy the initial condition y(0) = c for various values of c. For what values of c does / What are the possible value
> Use a computer algebra system to draw a direction field for the given differential equation. Get a printout and sketch on it the solution curve that passes through (0, 1). Then use the CAS to draw the solution curve and compare it with your sketch. y
> Find the radius of convergence and interval of convergence of the series. x" Σ 1 1 · 3 · 5 · .. 1:3. 5. ... · (2n – 1)
> Use a computer algebra system to draw a direction field for the given differential equation. Get a printout and sketch on it the solution curve that passes through (0, 1). Then use the CAS to draw the solution curve and compare it with your sketch. y
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point y' - x + y', (0, 0)
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point. у' — у+ ху, (0, 1)
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point. У — ху — х, (0, 1)
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point. у — у — 2х, (1, 0)
> Sketch a direction field for the differential equation. Then use it to sketch three solution curves. - y' = x - y + 1
> Sketch a direction field for the differential equation. Then use it to sketch three solution curves. y' = ły
> Use the direction field labeled III (above) to sketch the graphs of the solutions that satisfy the given initial conditions. (b) у(0) — 2.5 (с) у(0) — 3.5 %3D (а) у(0) — 1 %3D %3D
> Use the direction field labeled I (above) to sketch the graphs of the solutions that satisfy the given initial conditions. (а) у(0) — 1 () у(0) — 2.5 (с) у(0) — 3.5
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = sin x sin y yA IV -- -- -
> Find the radius of convergence and interval of convergence of the series. Σ n(In n)² n-2
> (a) For what values of k does the function y = cos k t satisfy the differential equation / (b) For those values of k, verify that every member of the family of functions y = A sin k t + B cos k t is also a solution.
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = 2 - y yA I --- %3D -- 2 * // 2.
> According to Newton’s Law of Universal Gravitation, the gravitational force on an object of mass m that has been projected vertically upward from the earth’s surface is where x = x(t) is the object’s
> Let A(t) be the area of a tissue culture at time t and let M be the final area of the tissue when growth is complete. Most cell divisions occur on the periphery of the tissue and the number of cells on the periphery is proportional to / So a reasonable m
> A model for tumor growth is given by the Gompertz equation where a and b are positive constants and V is the volume of the tumor measured in mm3. (a) Find a family of solutions for tumor volume as a function of time. (b) Find the solution that has an ini
> Allometric growth in biology refers to relationships between sizes of parts of an organism (skull length and body length, for instance). If L1(t) and L2(t) are the sizes of two organs in an organism of age t, then L1 and L2 satisfy an allometric law if t
> An object of mass m is moving horizontally through a medium which resists the motion with a force that is a function of the velocity; that is, where v = v(t) and s = s(t) represent the velocity and position of the object at time t, respectively. For exam
> Find the radius of convergence and interval of convergence of the series. (5х — 4)" Σ R-1
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> When a raindrop falls, it increases in size and so its mass at time t is a function of t, namely, m(t). The rate of growth of the mass is km(t) for some positive constant k. When we apply New ton’s Law of Motion to the raindrop, we get (mv) = tm, where v
> A tank contains 1000 L of pure water. Brine that contains 0.05 kg of salt per liter of water enters the tank at a rate of 5 L/min. Brine that contains 0.04 kg of salt per liter of water enters the tank at a rate of 10 L/min. The solution is kept thorough
> A vat with 500 gallons of beer contains 4% alcohol (by volume). Beer with 6% alcohol is pumped into the vat at a rate of 5 gal/min and the mixture is pumped out at the same rate. What is the percentage of alcohol after an hour?
> The air in a room with volume 180 m3 contains 0.15% carbon dioxide initially. Fresher air with only 0.05% carbon dioxide flows into the room at a rate of 2 m3ymin and the mixed air flows out at the same rate. Find the percentage of carbon dioxide in the
> A tank contains 1000 L of brine with 15 kg of dissolved salt. Pure water enters the tank at a rate of 10 L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank (a) after t minutes and (b) afte
> A certain small country has $10 billion in paper currency in circulation, and each day $50 million comes into the country’s banks. The government decides to introduce new currency by having the banks replace old bills with new ones whenever old currency
> A glucose solution is administered intravenously into the bloodstream at a constant rate r. As the glucose is added, it is converted into other substances and removed from the bloodstream at a rate that is proportional to the concentration at
> A sphere with radius 1 m has temperature 15 8C. It lies inside a concentric sphere with radius 2 m and temperature 25 8C. The temperature T(rd) at a distance r from the common center of the spheres satisfies the differential equation If we let S = dT/dr,
> In contrast to the situation of Exercise 40, experiments show that the reaction / satisfies the rate law and so for this reaction the differential equation becomes where x = [HBr] and a and b are the initial concentrations of hydrogen and bromine. (a) Fi
> In an elementary chemical reaction, single molecules of two reactants A and B form a molecule of the product C: A + B → C. The law of mass action states that the rate of reaction is proportional to the product of the concentrations of A
> Find the radius of convergence and interval of convergence of the series. n?x" Σ 2.4.6. .... (2n) n-1
> In formulated a model for learning in the form of the differential equation where P(t) measures the performance of someone learning a skill after a training time t, M is the maximum level of performance, and k is a positive constant. Solve this different
> In Exercise 9.2.28 we discussed a differential equation that models the temperature of a 95°C cup of coffee in a 20°C room. Solve the differential equation to find an expression for the temperature of the coffee at time t. Data from Exercise 9.2.28: In
> Solve the initial-value problem in Exercise 9.2.27 to find an expression for the charge at time t. Find the limiting value of the charge. Data from Exercise 9.2.27: The figure shows a circuit containing an electromotive force, a capacitor with a capaci
> Find a function f such that f(3) = 2 and (1? + 1)f"(1) + [f(1)]² + 1 = 0 t#1 ||
> An integral equation is an equation that contains an unknown function y(x) and an integral that involves y(x). Solve the given integral equation. y(x) у() — 4 + ("2у) 21/y(1) dt
> An integral equation is an equation that contains an unknown function y(x) and an integral that involves y(x). Solve the given integral equation. dt Уб) — 2 + ( ry(1) y(x) x>0
> An integral equation is an equation that contains an unknown function y(x) and an integral that involves y(x). Solve the given integral equation. y(x) [t - ty(1)] dt
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. 1 y = x + k
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. y
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. y? = kx' .3
> Find the radius of convergence and interval of convergence of the series. E n!(2x – 1)"
> Find the orthogonal trajectories of the family of curves. Use a graphing device to draw several members of each family on a common screen. x² + 2y? = k?
> (a) Use a computer algebra system to draw a direction field for the differential equation. Get a printout and use it to sketch some solution curves without solving the differential equation. (b) Solve the differential equation. (c) Use the CAS to draw se
> (a) Use a computer algebra system to draw a direction field for the differential equation. Get a printout and use it to sketch some solution curves without solving the differential equation. (b) Solve the differential equation. (c) Use the CAS to draw se
> Solve the differential equation y’ = x + y by making the change of variable u = x + y.
> Find the function f such that f’(x) = xf(x) – x and f(0) = 2.
> Find the radius of convergence and interval of convergence of the series. b" Σ -(х — а)", Ь>0 In n n-2
> Find an equation of the curve that passes through the point s0, 2d and whose slope at (x, y) is x/y.
> Find the solution of the differential equation that satisfies the given initial condition. dL kL² In t, L(1) = -1 dt
> Find the solution of the differential equation that satisfies the given initial condition. у' tan x — а + у, у(п/3) — а, 0<x<п/2
> Find the solution of the differential equation that satisfies the given initial condition. dP Pt , dt Р(1) — 2
> Find the solution of the differential equation that satisfies the given initial condition. x In x = y(1 + /3 + y² ) y', y(1) = 1
> Find the solution of the differential equation that satisfies the given initial condition. dy x + 3y' /x? + T = 0, y(0) = 1 dx
> Find the solution of the differential equation that satisfies the given initial condition. du 21 + sec?t u(0) = -5 %3D dt 2u
> Find the solution of the differential equation that satisfies the given initial condition. dy x sin x y(0) dx y
> Find the solution of the differential equation that satisfies the given initial condition. dy - хе', у(0) — 0 dx
> Solve the differential equation. dz + ettz = 0 dt
> Find the radius of convergence and interval of convergence of the series. - (х — а)", Ь> 0 Σ b" n-1
> Solve the differential equation. dp uP. = t°p – p + t² – 1 dt
> Solve the differential equation. dH_ /T + R² In H RH² dR
> Solve the differential equation. de t sec 0 dt Oe“

