Question: An experiment was conducted to determine whether
An experiment was conducted to determine whether surface finish has an effect on the endurance limit of steel. There is a theory that polishing increases the average endurance limit (for reverse bending). From a practical point of view, polishing should not have any effect on the standard deviation of the endurance limit, which is known from numerous endurance limit experiments to be 4000 psi. An experiment was performed on 0.4% carbon steel using both unpolished and polished smooth-turned specimens.
The data are as follows:
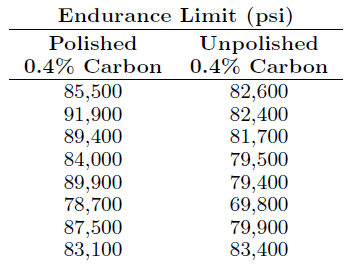
Find a 95% confidence interval for the difference between the population means for the two methods, assuming that the populations are approximately normally distributed.
Transcribed Image Text:
Endurance Limit (psi) Unpolished 0.4% Carbon Polished 0.4% Carbon 85,500 91,900 89,400 84,000 89,900 78,700 87,500 83,100 82,600 82,400 81,700 79,500 79,400 69,800 79,900 83,400
> Identify the surfaces whose equations are given. (a). θ = π/4 (b). φ = π/4
> The spherical coordinates of a point are (8, π/4, π/6). Find the rectangular and cylindrical coordinates of the point.
> The rectangular coordinates of a point are (2, 2, -1). Find the cylindrical and spherical coordinates of the point.
> The cylindrical coordinates of a point are (2√(3 ), π/3, 2). Find the rectangular and spherical coordinates of the point.
> Write ∬R f (x, y) dA as an iterated integral, where R is the region shown and f is an arbitrary continuous function on R. y4 4, R -4 4 x
> Write ∬R f (x, y) dA as an iterated integral, where R is the region shown and f is an arbitrary continuous function on R. y. 4 R -4 -2 0 4 x 2.
> Calculate the iterated integral. ∫_0^1 ∫_0^y ∫_x^16xyz dz dx dy
> Calculate the iterated integral. ∫_0^π ∫_0^1 √(1-y^2 ) y sin x dz dy dx
> Calculate the iterated integral. ∫_0^1 ∫_x^(e^x) (3xy^2) dy dx
> Calculate the iterated integral. ∫_0^1 ∫_0^x (x^2) dy dx
> The plane x/a+y/b+z/c = 1 a > 0, b > 0, c > 0 cuts the solid ellipsoid into two pieces. Find the volume of the smaller piece. a? < 1 +
> Calculate the iterated integral. ∫_0^1 ∫_0^1 (ye^xy dx dy
> The Taylor polynomial approximation to functions of one variable that we discussed in Chapter 11 can be extended to functions of two or more variables. Here we investigate quadratic approximations to functions of two variables and use them to give insigh
> Find and sketch the domain of the function. f (x, y) = √(4 - x^2 - y^2 ) + √(1 - x^2 )
> A contour map is shown for a function f on the square R = [0, 3] × [0, 3]. Use a Riemann sum with nine terms to estimate the value of ∬R f (x, y) dA. Take the sample points to be the upper right corners of the squares.
> If f (x, y) has two local maxima, then f must have a local minimum. Find a linear approximation to the temperature function T (x, y) in Exercise 11 near the point (6, 4). Then use it to estimate the temperature at the point (5, 3.8). Exercise 11: If f
> If (2, 1) is a critical point of f and fxx (2, 1) fyy (2, 1) < [ fxy (2, 1)]2 Evaluate the limit or show that it does not exist. lim┬((x,y)→(1,1))2xy/(x^2+2y^2 )
> Make a rough sketch of a contour map for the function whose graph is shown. If f has a local minimum at (a, b) and f is differentiable at (a, b), then =f (a, b) = 0.
> If f (x, y) = ln y, then ∆f (x, y) = 1/y. Evaluate the limit or show that it does not exist. lim┬((x,y)→(1,1))2xy/(x^2+2y^2 )
> If f (x, y) = sin x + sin y, then -√2 A metal plate is situated in the xy-plane and occupies the rectangle 0 (a). Estimate the values of the partial derivatives Tx (6, 4) and Ty (6, 4). What are the units? (b). Estimate the value of
> If z = y + f (x2 - y2), where f is differentiable, show that Y ∂z/∂x + ∂z/∂y + = x
> Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint. f(x, y, z) = x* + y* + 24; x' + y? + z? = 1
> Use a tree diagram to write out the Chain Rule for the case where w = f (t, u, v), t = t (p, q, r, s), u = u (p, q, r, s), and v = v (p, q, r, s) are all differentiable functions.
> Suppose z = f (x, y), where x = g (s, t), y = h (s, t), t (1, 2) = 3, gs (1, 2) = -1, gt (1, 2) = 4, h (1, 2) = 6, hs (1, 2) = -5, ht (1, 2) = 10, fx (3, 6) = 7, and fy (3, 6) = 8. Find ∂z/∂s and ∂z/∂t when s = 1 and t = 2.
> If v = x2 sin y + yexy, where x = s + 2t and y = st, use the Chain Rule to find ∂v/∂s and ∂v/∂t when s = 0 and t = 1.
> If u = x2y3 + z4, where x = p + 3p2, y = pep, and z = p sin p, use the Chain Rule to find du/dp.
> Find the linear approximation of the function f (x, y, z) = x3 √(y^2+ z^2 ) at the point (2, 3, 4) and use it to estimate the number (1.98)3 √((3.01)^2 + (3.97)^2 ).
> Find du if u = ln (1 + se2t).
> Sketch the graph of the function. f (x, y) = 1 - y2
> If z = sin (x + sin t), show that az az ax ax at az a'z at ax?
> If z = xy + xey/x, show that x∂z/∂x + y ∂z/∂y = xy + z.
> Find all second partial derivatives of f. v = r cos (s + 2t)
> Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint. f(x, y, z) = x² + y² + z²; x* + y* + z* = 1
> Suppose that f is continuous on a disk that contains the point (a, b). Let Dr be the closed disk with center (a, b) and radius r. Use the Mean Value Theorem for double integrals (see Exercise 58) to show that Exercise 58: The Mean Value Theorem for do
> Find all second partial derivatives of f. f (x, y, z) = xkylzm
> Find all second partial derivatives of f. z = xe-2y
> Use the transformation x = u2, y = v2, z = w2 to find the volume of the region bounded by the surface √x + √y + √z = 1 and the coordinate planes.
> Use the transformation u = x - y, v = x + y to evaluate where R is the square with vertices (0, 2), (1, 1), (2, 2), and (1, 3). х — у -dA х+у
> Give five other iterated integrals that are equal to ∫_0^2 ∫_0^(y^3) ∫_0^(y^2) f (x,y,z) dz dx dy
> Rewrite the integral as an iterated integral in the order dx dy dz. *1-y °f(x, y, z) dz dy dx Jo
> Find all second partial derivatives of f. f (x, y) = 4x3 - xy2
> Find the first partial derivatives. S (u, v, w) = u arctan (v √w)
> Find the center of mass of the solid tetrahedron with vertices (0, 0, 0), (1, 0, 0), (0, 2, 0), (0, 0, 3) and density function ρ (x, y, z) = x2 + y2 + z2.
> Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint. f(x, y, z) = In(x² + 1) + In(y² + 1) + In(z² + 1)
> Pictured are a contour map of f and a curve with equation t (x, y) = 8. Estimate the maximum and minimum values of f subject to the constraint that t (x, y) = 8. Explain your reasoning. yA glx, y) = 8 40 50 60 70 30 20 10
> An alternative form of estimation is accomplished through the method of moments. This method involves equating the population mean and variance to the corresponding sample mean ¯x and sample variance s2 and solving for the parameters, the results being t
> It is argued that the resistance of wire A is greater than the resistance of wire B. An experiment on the wires shows the following results (in ohms): Assuming equal variances, what conclusions do you draw? Justify your answer. Wire B 0.135 Wire A
> A manufacturer of electric irons produces these items in two plants. Both plants have the same suppliers of small parts. A saving can be made by purchasing thermostats for plant B from a local supplier. A single lot was purchased from the local supplier,
> An anthropologist is interested in the proportion of individuals in two Indian tribes with double occipital hair whorls. Suppose that independent samples are taken from each of the two tribes, and it is found that 24 of 100 Indians from tribe A and 36 of
> The Department of Civil Engineering at Virginia Tech compared a modified (M-5 hr) assay technique for recovering fecal coliforms in storm water runoff from an urban area to a most probable number (MPN) technique. A total of 12 runoff samples were collect
> A health spa claims that a new exercise program will reduce a person’s waist size by 2 centimeters on average over a 5-day period. The waist sizes, in centimeters, of 6 men who participated in this exercise program are recorded before a
> A study was undertaken at Virginia Tech to determine if fire can be used as a viable management tool to increase the amount of forage available to deer during the critical months in late winter and early spring. Calcium is a required element for plants a
> It is claimed that a new diet will reduce a person’s weight by 4.5 kilograms on average in a period of 2 weeks. The weights of 7 women who followed this diet were recorded before and after the 2-week period. Test the claim about the d
> According to the Roanoke Times, McDonald’s sold 42.1% of the market share of hamburgers. A random sample of 75 burgers sold resulted in 28 of them being from McDonald’s. Use material in Section 9.10 to determine if this information supports the claim in
> Regular consumption of presweetened cereals contributes to tooth decay, heart disease, and other degenerative diseases, according to studies conducted by Dr. W. H. Bowen of the National Institute of Health and Dr. J. Yudben, Professor of Nutrition and Di
> Consider two estimators of σ2 for a sample x1, x2, . . . , xn, which is drawn from a normal distribution with mean μ and variance σ2. The estimators are the unbiased estimator s2 = 1 the maximum likelihood estimator
> Consider the observation X from the negative binomial distribution given in Section 5.4. Find the maximum likelihood estimator for p, assuming k is known.
> Consider a hypothetical experiment where a man with a fungus uses an antifungal drug and is cured. Consider this, then, a sample of one from a Bernoulli distribution with probability function where p is the probability of a success (cure) and q = 1 &ac
> Consider the independent observations x1, x2, . . . , xn from the gamma distribution discussed in Section 6.6. (a) Write out the likelihood function. (b) Write out a set of equations that, when solved, give the maximum likelihood estimators of α and β.
> Consider a random sample of x1, . . . , xn from a uniform distribution U(0, θ) with unknown parameter θ, where θ > 0. Determine the maximum likelihood estimator of θ.
> Consider a random sample of x1, x2, . . . , xn observations from a Weibull distribution with parameters α and β and density function / (a) Write out the likelihood function. (b) Write out the equations that, when solved, give the maximum likelihood
> Consider a random sample of x1, . . . , xn coming from the gamma distribution discussed in Section 6.6. Suppose the parameter α is known, say 5, and determine the maximum likelihood estimation for parameter β.
> Consider the lognormal distribution with the density function given in Section 6.9. Suppose we have a random sample x1, x2, . . . , xn from a lognormal distribution. (a) Write out the likelihood function. (b) Develop the maximum likelihood estimators o
> Suppose that there are n trials x1, x2, . . . , xn from a Bernoulli process with parameter p, the probability of a success. That is, the probability of r successes is given by Work out the maximum likelihood estimator for the parameter p. (:)p"(1
> Construct a 95% confidence interval for σ2A/σ2B in Exercise 9.49 on page 295. Should the equal-variance assumption be used? Exercise 9.49: Two different brands of latex paint are being considered for use. Fifteen specimens of each
> An efficiency expert wishes to determine the average time that it takes to drill three holes in a certain metal clamp. How large a sample will she need to be 95% confident that her sample mean will be within 15 seconds of the true mean? Assume that it is
> Construct a 90% confidence interval for σ21/σ22 in Exercise 9.46 on page 295. Should we have assumed σ21 = σ22 in constructing our confidence interval for μI − μII?
> Construct a 90% confidence interval for σ21/σ22 in Exercise 9.43 on page 295. Were we justified in assuming that σ21 ≠ σ22 when we constructed the confidence interval for μ1 − μ2? Exercise 9.43: A taxi company is trying to decide whether to purchase bra
> Construct a 98% confidence interval for σ1/σ2 in Exercise 9.42 on page 295, where σ1 and σ2 are, respectively, the standard deviations for the distances traveled per liter of fuel by the Volkswagen and Toyota mini-trucks. Exercise 9.42: An experiment re
> Construct a 90% confidence interval for σ in Exercise 9.13 on page 283. Exercise 9.13: A random sample of 12 shearing pins is taken in a study of the Rockwell hardness of the pin head. Measurements on the Rockwell hardness are made for each of the 12, y
> Construct a 99% confidence interval for σ in Exercise 9.12 on page 283. Exercise 9.12: A random sample of 10 chocolate energy bars of a certain brand has, on average, 230 calories per bar, with a standard deviation of 15 calories. Construct a 99% confid
> Construct a 99% confidence interval for σ2 in Exercise 9.11 on page 283. Exercise 9.11: A machine produces metal pieces that are cylindrical in shape. A sample of pieces is taken, and the diameters are found to be 1.01, 0.97, 1.03, 1.04, 0.99, 0.98, 0.9
> Construct a 95% confidence interval for σ2 in Exercise 9.9 on page 283. Exercise 9.9: Regular consumption of presweetened cereals contributes to tooth decay, heart disease, and other degenerative diseases, according to studies conducted by Dr. W. H. Bow
> A random sample of 20 students yielded a mean of ¯x = 72 and a variance of s2 = 16 for scores on a college placement test in mathematics. Assuming the scores to be normally distributed, construct a 98% confidence interval for σ2.
> A manufacturer of car batteries claims that the batteries will last, on average, 3 years with a variance of 1 year. If 5 of these batteries have lifetimes of 1.9, 2.4, 3.0, 3.5, and 4.2 years, construct a 95% confidence interval for σ2 and decide if the
> According to USA Today (March 17, 1997), women made up 33.7% of the editorial staff at local TV stations in the United States in 1990 and 36.2% in 1994. Assume 20 new employees were hired as editorial staff. (a) Estimate the number that would have been w
> How large a sample is needed in Exercise 9.3 if we wish to be 95% confident that our sample mean will be within 0.0005 inch of the true mean? Exercise 9.3 Many cardiac patients wear an implanted pacemaker to control their heartbeat. A plastic connector
> A survey of 1000 students found that 274 chose professional baseball team A as their favorite team. In a similar survey involving 760 students, 240 of them chose team A as their favorite. Compute a 95% confidence interval for the difference between the p
> In the study Germination and Emergence of Broccoli, conducted by the Department of Horticulture at Virginia Tech, a researcher found that at 5◦ C, 10 broccoli seeds out of 20 germinated, while at 15◦ C, 15 out of 20 germinated. Compute a 95% confidence i
> A clinical trial was conducted to determine if a certain type of inoculation has an effect on the incidence of a certain disease. A sample of 1000 rats was kept in a controlled environment for a period of 1 year, and 500 of the rats were given the inocul
> Ten engineering schools in the United States were surveyed. The sample contained 250 electrical engineers, 80 being women; 175 chemical engineers, 40 being women. Compute a 90% confidence interval for the difference between the proportions of women in th
> A certain geneticist is interested in the proportion of males and females in the population who have a minor blood disorder. In a random sample of 1000 males, 250 are found to be afflicted, whereas 275 of 1000 females tested appear to have the disorder.
> A study is to be made to estimate the proportion of residents of a certain city and its suburbs who favor the construction of a nuclear power plant near the city. How large a sample is needed if one wishes to be at least 95% confident that the estimate i
> A study is to be made to estimate the percentage of citizens in a town who favor having their water fluoridated. How large a sample is needed if one wishes to be at least 95% confident that the estimate is within 1% of the true percentage?
> A conjecture by a faculty member in the microbiology department at Washington University School of Dental Medicine in St. Louis, Missouri, states that a couple of cups of either green or oolong tea each day will provide sufficient fluoride to protect you
> How large a sample is needed in Exercise 9.52 if we wish to be 98% confident that our sample proportion will be within 0.05 of the true proportion defective? Exercise 9.52: Compute 95% confidence intervals, using both methods on page 297, for the propor
> How large a sample is needed if we wish to be 99% confident that our sample proportion in Exercise 9.51 will be within 0.05 of the true proportion of homes in the city that are heated by oil? Exercise 9.51: In a random sample of 1000 homes in a certain
> How large a sample is needed in Exercise 9.2 if we wish to be 96% confident that our sample mean will be within 10 hours of the true mean? Exercise 9.2 An electrical firm manufactures light bulbs that have a length of life that is approximately normally
> How large a sample is needed if we wish to be 96% confident that our sample proportion in Exercise 9.53 will be within 0.02 of the true fraction of the voting population? Exercise 9.53: (a) A random sample of 200 voters in a town is selected, and 114 ar
> In the newspaper article referred to in Exercise 9.57, 32% of the 1600 adults polled said the U.S. space program should emphasize scientific exploration. How large a sample of adults is needed for the poll if one wishes to be 95% confident that the estim
> (a) According to a report in the Roanoke Times & World-News, approximately 2/3 of 1600 adults polled by telephone said they think the space shuttle program is a good investment for the country. Find a 95% confidence interval for the proportion of America
> A geneticist is interested in the proportion of African males who have a certain minor blood disorder. In a random sample of 100 African males, 24 are found to be afflicted. (a) Compute a 99% confidence interval for the proportion of African males who ha
> A new rocket-launching system is being considered for deployment of small, short-range rockets. The existing system has p = 0.8 as the probability of a successful launch. A sample of 40 experimental launches is made with the new system, and 34 are succes
> A manufacturer of MP3 players conducts a set of comprehensive tests on the electrical functions of its product. All MP3 players must pass all tests prior to being sold. Of a random sample of 500 MP3 players, 15 failed one or more tests. Find a 90% confid
> (a) A random sample of 200 voters in a town is selected, and 114 are found to support an annexation suit. Find the 96% confidence interval for the fraction of the voting population favoring the suit. (b) What can we assert with 96% confidence about the p
> Compute 95% confidence intervals, using both methods on page 297, for the proportion of defective items in a process when it is found that a sample of size 100 yields 8 defectives.
> In a random sample of 1000 homes in a certain city, it is found that 228 are heated by oil. Find 99% confidence intervals for the proportion of homes in this city that are heated by oil using both methods presented on page 297.
> Two levels (low and high) of insulin doses are given to two groups of diabetic rats to check the insulin binding capacity, yielding the following data: Low dose: n1 = 8 ¯x1 = 1.98 s1 = 0.51 High dose: n2 = 13 ¯x2 = 1.30 s2 = 0.35 Assume that the variance
> A random sample of 100 automobile owners in the state of Virginia shows that an automobile is driven on average 23,500 kilometers per year with a standard deviation of 3900 kilometers. Assume the distribution of measurements to be approximately normal. (
> Two different brands of latex paint are being considered for use. Fifteen specimens of each type of paint were selected, and the drying times, in hours, were as follows: Assume the drying time is normally distributed with σA = σB.

