Question: Compare the death rates per 1000 people

> Refer to the data in Exercise 29. a. If two selections are made with replacement, find the probability that both people refused to respond. b. If two selections are made without replacement, find the probability that both people refused to respond. c. Co

> Refer to the following table summarizing results from a study of 1205 people who either responded to or refused to answer survey questions (based on data from “I Hear You Knocking but You Can’t Come In,â€&#1

> Refer to the data in Exercise 27. a. If two selections are made with replacement, find the probability that both people improved. b. If two selections are made without replacement, find the probability that both people improved. c. Compare the results fr

> In a clinical trial of an allergy medication, 120 people are treated with the medication and 100 other people are given a placebo. A control group consists of 80 people who are given neither the medication nor the placebo. The number of people in each gr

> If two different pedestrian deaths are randomly selected, find the probability that in both cases the pedestrians were intoxicated.

> If two different pedestrian deaths are randomly selected, find the probability that they both involved intoxicated drivers.

> If one of the pedestrian deaths is randomly selected, find the probability that the driver was intoxicated or the pedestrian was not intoxicated.

> If r = 1 or r = -1, then all points in the scatterplot lie directly on the best-fit line.

> If one of the pedestrian deaths is randomly selected, find the probability that the pedestrian was intoxicated or the driver was not intoxicated.

> If one of the pedestrian deaths is randomly selected, find the probability that the pedestrian was not intoxicated or the driver was not intoxicated.

> If one of the pedestrian deaths is randomly selected, find the probability that the pedestrian was intoxicated or the driver was intoxicated.

> If a defendant is randomly selected, what is the probability that the defendant entered a guilty plea and was not sent to prison? Source: Brereton and Casper, “Does It Pay to Plead Guilty? Differential Sentencing and the Functioning of

> If a defendant is randomly selected, what is the probability that the defendant entered a guilty plea and was sent to prison? Source: Brereton and Casper, “Does It Pay to Plead Guilty? Differential Sentencing and the Functioning of the

> If two different defendants are randomly selected, what is the probability that they both were sentenced to prison? Source: Brereton and Casper, “Does It Pay to Plead Guilty? Differential Sentencing and the Functioning of the Criminal C

> If two different defendants are randomly selected, what is the probability that they both entered guilty pleas? Source: Brereton and Casper, “Does It Pay to Plead Guilty? Differential Sentencing and the Functioning of the Criminal Court

> What is the probability that a randomly selected defendant either pled not guilty or was not sent to prison? Source: Brereton and Casper, “Does It Pay to Plead Guilty? Differential Sentencing and the Functioning of the Criminal Courts,&

> What is the probability that a randomly selected defendant either pled guilty or was sent to prison? Source: Brereton and Casper, “Does It Pay to Plead Guilty? Differential Sentencing and the Functioning of the Criminal Courts,â&#

> A pollster plans to call adults. She has a list of names and numbers of 100 adults, consisting of 60 males and 40 females. She will make random selections and will not call the same person more than once. a. Consider the event of getting a male on the fi

> If r = 0.200, then r2 = 0.040 and 4% of the plotted points lie on the best-fit line.

> The 50 songs on a smart phone consist of 15 that are rock, 20 that are jazz, and 15 that are country. Selections are played randomly and can be repeated. What is the probability of each of the following events? a. The first two selections are both rock.

> A study of hunting injuries and the wearing of hunter orange clothing showed that among 123 hunters injured when mistaken for game, 6 were wearing orange (based on data from the Centers for Disease Control and Prevention). If a follow-up study begins wit

> A programmer is instructed to create a password consisting of two different digits. What is the probability that the password is 12?

> A couple plans to have four children. Find the probability that the first three children are girls and the last child is a boy.

> Assume that boys and girls are equally likely and that the gender of a child is independent of the gender of any brothers or sisters. If a couple already has three girls, find the probability of getting a girl when their fourth baby is born.

> The probability of your winning your state’s lottery this week is not affected by whether you won that same lottery last week.

> The probability of rolling a die and getting an even number is 1/2, and the probability of getting an odd number is 1/2, so the probability of getting a number that is even or odd is 1/2 + 1/2 = 1.

> The probability of flipping a coin and getting heads is 1/2. The probability of rolling a die and getting a 2 is 1/6. When flipping a coin and rolling a die at the same time, the probability of getting heads or a 2 is 1/2 + 1/6 = 3/6 + 1/6 = 4/6, or 2/3.

> Because the numbers 5, 17, 18, 27, 36, and 41 were drawn in the last lottery, you should not bet on them in the next lottery because they are now less likely to be drawn.

> No one can succeed in selling a product that will kill thousands of people per year.

> Fill in the blank: If r = 0.900, then ___% of the variation in the response variable y can be explained by the linear relationship between x and y as described by the best-fit line.

> Based on recent data, a 20-year-old person in the United States has a life expectancy of about 60 years. What does that mean?

> What is life expectancy? Does a 30-year-old person have the same life expectancy as a 20-year-old person? Why or why not?

> What are vital statistics? What does it mean to say that the current U.S. birth rate is 13.2 per 1000 people?

> What is travel risk? Give an example. Can you easily compare different risk rates?

> What would the life expectancy for men be in 2100? Do you think this calculation gives a more or less realistic estimate of life expectancy in 2100 than was found in Example 5? Explain.

> What would the life expectancy for women be in 2100? Do you think this calculation gives a more or less realistic estimate of life expectancy in 2100 than was found in Example 5? Explain.

> Based on current life expectancy data, to what age is the average 80-year-old expected to live? Figure 6.13 (a) The overall U.S. death rate (deaths per 1000 people) for different ages. (b) Life expectancy (the number of additional years of life that c

> Based on current life expectancy data, to what age is the average 40-year-old expected to live? Figure 6.13 (a) The overall U.S. death rate (deaths per 1000 people) for different ages. (b) Life expectancy (the number of additional years of life that c

> Estimate the death rate for 25-year-olds. If the population of people this age is 42 million, how many people of this age can be expected to die in a year? Figure 6.13 (a) The overall U.S. death rate (deaths per 1000 people) for different ages. (b) L

> Estimate the death rate for 60-year-olds. If the population of people this age is about 14 million, how many people of this age can be expected to die in a year? Figure 6.13 (a) The overall U.S. death rate (deaths per 1000 people) for different ages.

> Refer again to the scatterplot in Figure 7.24. Does there appear to be a significant correlation between the two variables? Figure 7.24.

> If you lived in a typical city of 500,000, how many people would you expect to die due to chronic respiratory diseases in a year? Source: Centers for Disease Control and Prevention; data for 2014.

> If you lived in a typical city of 500,000, how many people would you expect to die due to a stroke in a year?

> What is the death rate due to heart disease in deaths per 100,000 of the population? Source: Centers for Disease Control and Prevention; data for 2014.

> What is the death rate due to Alzheimer’s disease in deaths per 100,000 of the population? Source: Centers for Disease Control and Prevention; data for 2014.

> Find the death rate of 20-year-olds per 100,000 people during the year. How many 20-year-olds would be expected to die out of 10,000 people?

> Find the death rate of 19-year-olds per 100,000 people during the year. How many 19-year-olds would be expected to die out of 10,000 people?

> Based on current life expectancy data, how many years is a randomly selected 18-year-old expected to live beyond his or her 18th birthday?

> Based on current life expectancy data, how many years is a randomly selected 20-year-old expected to live beyond his or her 20th birthday?

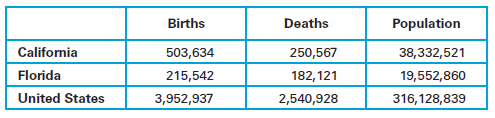
> Compare the death rates per 1000 people for California and Florida. Identify a reason for the difference.

> Estimate the correlation coefficient for the data points in the scatterplot in Figure 7.24. Figure 7.24.

> Find the birth rate per 1000 people for California.

> Find the birth rate per 1000 people for the United States.

> For the year 2014, find the fatality rate in deaths per passenger mile (instead of per billion passenger miles). Why don’t we report the fatality rate in units of deaths per passenger mile?

> For each of the three years, find the fatality rate in deaths per million passengers. On the basis of those rates, which year was the safest? Why?

> For each of the three years, find the fatality rate in deaths per billion passenger miles. On the basis of those rates, which year was the safest? Why?

> For each of the three years, find the fatality rate in deaths per 1000 departures. On the basis of those rates, which year was the safest? Why?

> A 60-year-old has a shorter life expectancy than a 20-year-old.

> Your life expectancy is the major factor in determining how long you live.

> The death rate for motorcycle accidents is much higher than the death rate for automobile accidents, so more people must die in motorcycle accidents than in car accidents.

> What is the gambler’s fallacy? Give an example.

> For a collection of 50 pairs of sample data values, the correlation coefficient is found to be r  -0.900. Which of the following statements best describes the relationship between the two variables? a. There is no correlation. b. There is a weak positiv

> What is an expected value, and how is it computed? Should we always expect to realize the expected value? Why or why not?

> In terms of the law of large numbers, explain why you should not be surprised to see 6 heads in 10 tosses of a fair coin, but you should be surprised to see 600 heads in 1000 tosses of the same coin.

> What is the law of large numbers? Can it be applied to a single observation or experiment? Explain.

> Can You Catch Up? Suppose that you toss a fair coin 100 times, getting 38 heads and 62 tails, which is 24 more tails than heads. a. Explain why, on your next toss, the difference in the numbers of heads and tails is as likely to grow to 25 as it is to sh

> In 1953, a French economist named Maurice Allais conducted a survey of how people assess risk. Here are two scenarios that he used, each of which required people to choose between two options. Decision 1 Option A: 100% chance of gaining $1,000,000 Optio

> Reader’s Digest ran a sweepstakes in which prizes were listed along with the chances of winning: $1,000,000 (1 chance in 90,000,000), $100,000 (1 chance in 110,000,000), $25,000 (1 chance in 110,000,000), $5,000 (1 chance in 36,667,000), and $2,500 (1 ch

> Football teams have the option of trying to score either 1 or 2 extra points after a touchdown. A team scores 1 point by kicking the ball through the goal posts or 2 points by running or passing the ball across the goal line. For a recent year in the NFL

> In New Jersey’s Pick 4 lottery, you pay 50¢ to select a sequence of four digits, such as 2273, from the 10,000 different possible four-digit sequences. If you select the same sequence of four digits that are drawn, you win and collect $2788. What is your

> When you give a casino $20 for a bet on the “pass line” in a dice game, there is a 251/495 probability that you will lose $20 and there is a 244/495 probability that you will make a net gain of $20. (If you win, the casino gives you $20 and you get to ke

> As shown in Figure 6.11, a roulette wheel has 38 numbers, with 18 odd numbers (black) and 18 even numbers (red), as well as 0 and 00 (which are green). If you bet $5 that the outcome is an odd number, the probability of losing the $5 is 20/38 and the pro

> Which of the following are likely to have a correlation? a. Amounts donated to charities in a year and annual incomes. b. Hat sizes and annual incomes of randomly selected adults. c. Braking reaction times and weights of randomly selected adults. d. Heig

> You arrive at a bus stop randomly, and all arrival times are equally likely. The bus arrives regularly every 24 minutes without delay. What is the expected value for your waiting time?

> There is a 0.9968 probability that a randomly selected 50-year-old female will live through the year. A life insurance company charges $226 for insuring that the female will live through the year. If she does not survive the year, the policy pays out $50

> There is a 0.9986 probability that a randomly selected 30-year-old male will live through the year. A life insurance company charges $161 for insuring that the male will live through the year. If he does not survive the year, the policy pays out $100,000

> If you bet $1 in Kentucky’s Pick 4 lottery, you either lose $1 or gain $4999. (The winning prize is $5000, but your $1 bet is not returned, so the net gain is $4999.) The game is played by selecting a four-digit number between 0000 and 9999. What is the

> Suppose you are offered this opportunity: You can place a bet of $10 and someone else tosses a coin. You win an additional $15 if heads occurs, and you lose your $10 if tails occurs. What is the expected value of this game? Should you play?

> A person who has a habit of driving fast has never had a traffic citation. What does it mean to say that “the law of averages will catch up with him”? Is it true? Explain.

> In analyzing genders of newborns, assume that boys and girls are equally likely. Among 500 births, should we expect exactly 250 boys and 250 girls? As the number of births increases, what does the law of large numbers tell us about the proportion of girl

> I haven’t won in my last 25 pulls on the slot machine, so I’m due to win on the next couple of pulls.

> For the California Daily 3 lottery, in which you pick three numbers, it is better to select the numbers 5-3-9 than the numbers 1-2-3, because 5-3-9 is more random.

> For a $1 “straight” bet in the California Daily 3 lottery, the expected return is 64¢, so betting a dollar for fun is okay, but it is unwise to bet much money on this lottery.

> If a best-fit line is inserted in a scatterplot, it must pass through every point on the graph.

> For a typical lottery, the expected value of a ticket is less than the cost of a ticket.

> What is a probability distribution? Briefly describe a format that is used to display a probability distribution.

> Briefly describe the theoretical, relative frequency, and subjective methods for finding probabilities. Give an example of each.

> What does it mean when we write P(A)? What is the possible range of values for P(A), and why?

> Distinguish between an outcome and an event in probability. Give an example in which the same event can occur via two or more outcomes.

> The histogram in Figure 6.9 shows the distribution of “Mega” numbers (possible values range from 1 to 27) that were drawn in 1639 separate plays of the California lottery game Mega Millions. a. Assuming the lottery dra

> After constructing a table that is similar to Table 6.2 and shows all possible outcomes of tossing four coins at once, find the following. a. Find the probability that all four tosses are the same (all heads or all tails). b. Find the probability that th

> In a clinical trial in which 73 patients with carpal tunnel syndrome were treated with surgery, 67 had successful treatment (based on data from “Splinting vs. Surgery in the Treatment of Carpal Tunnel Syndrome” by Gerritsen et al., Journal of the America

> Halfway through the season, a basketball player has made 72% of her free throws. What is the probability that her next free throw will be successful?

> What is the probability of a 100-year flood happening this year?

> Every possible correlation coefficient must lie between the values of ____ and____.

> After recording the forecasts of your local meteorologist for 30 days, you conclude that she gave a correct forecast for 26 days. What is the probability that her next forecast will be correct?

> Suppose you randomly select a family with four children. Assume that births of boys and girls are equally likely. a. How many birth orders are possible? List them in a probability distribution table. b. What is the probability that the family has four ch

> Suppose you randomly select a family with three children. Assume that births of boys and girls are equally likely. a. How many birth orders are possible? List them in a probability distribution table. b. What is the probability of two boys and a girl? c.

> The New England College of Medicine uses an admissions test with many multiple-choice questions, each with five possible answers, only one of which is correct. If you guess randomly on every question, what score might you expect to get? (Express the answ

> A bag contains 13 red M&Ms, 25 orange M&Ms, 8 yellow M&Ms, 8 brown M&Ms, 27 blue M&Ms, and 19 green M&Ms. When randomly selecting one M&M, what is the probability of drawing a red M&M? A blue M&M? A yellow M&M? An M&M that is not orange?