Question: Consider Example 12-4 concerning the efficiency
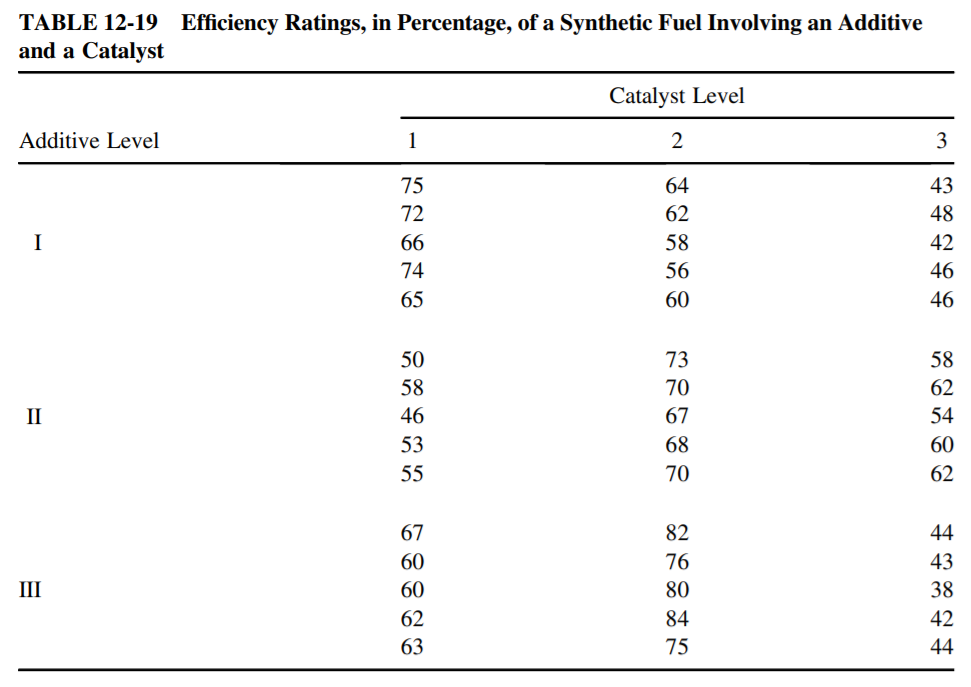
Consider Example 12-4 concerning the efficiency of synthetic fuel for which the factors are an additive and a catalyst. The original data are given in Table 12-19. The experiment is conducted using only five randomly chosen automobiles (A, B, C, D, and E). Each treatment is used on each automobile. The reason for choosing only five automobiles and replicating the experiment is to eliminate any variation in the fuel efficiencies that might arise due to differences in the automobiles. The data in Table 12-19 is interpreted as follows. For additive level I and catalyst level 1, the response value is 75 for automobile A, 72 for automobile B, and so forth. Similar interpretations hold for the other treatments.
(a) What is your conclusion regarding the significance of the factors or their interactions? Test at the 5% level of significance.
(b) Find a 95% confidence interval for the mean efficiency when the additive is at level I and the catalyst is at level 2. (c) Find a 95% confidence interval for the difference in the treatment means when the additive is at level I and the catalyst is at level 3 versus when the additive is at level II and the catalyst is at level 3. What is your conclusion?
(d) What levels of additive and catalyst would you prefer to choose?
(e) Was it beneficial to select only five automobiles and replicate the treatments on only those automobiles? Test at the 5% level of significance.
Data from Example 12-4:
In a study on the effectiveness of synthetic automobile fuels, two factors are of importance. Factor A is an additive that is to be tested at three levels of use in successively increasing amounts. Factor B is a catalyst, for which three levels of use (1, 2, and 3, representing successively increasing amounts) are also to be tested. Forty-five automobiles are randomly selected for the study, and each of the nine treatments is randomly used in five different automobiles. Table 12-19 shows the efficiency ratings, in percentage, of the treatments.
(a) At a level of significance of 5%, what can we conclude about the significance of the factors?
Solution:
The problem involves two factors using a completely randomized design. Using the raw data as given in Table 12-19, the summary information shown in Table 12-20 is computed.
Data from Table 12-19:
> Based on historical data, it is estimated that 12% of new products will obtain a profitable market share. However, if two products are newly introduced in the same year, there is only a 5% chance of both products becoming profitable. A company is plannin
> An automobile manufacturing company is attempting to cope with rising health care costs of its employees. It offers three types of plans. Based on a random sample of 200 employees selected last year, Table 5-11 shows the number who selected each plan. Th
> Percentage investment in new-product development is monitored for a pharmaceutical company by quarter. The observations are listed row wise: (a) Can we conclude that the sequence of investment percentages is random? Use α= 0.05. (b) Is ther
> The pH values of a dye for 30 samples taken consecutively over time are listed row wise: (a) Can we conclude that the sequence of pH values over time is non-random? Use α = 0.05. (b) Assume that dyes are produced in batches, with 10 random
> Using the call waiting time of customer data in Exercise 5-9, construct a stem-and-leaf plot. Construct a box plot and comment on the distribution. Are there any outliers? Construct a 95% confidence interval for the median. Data from Exercise 5-9: A ran
> A random sample of 50 observations on the waiting time (in seconds) of customers before speaking to a representative at a call center is as follows: (a) Construct a histogram and comment on the process. (b) What assumptions are necessary to test if the m
> A remote control unit has 40 components in series. The reliability of each component is 0.9994. What is the reliability of the remote control unit? If a redesign has 25 components in series, what is the reliability of the unit?
> A retail company has information on the time taken (in days) to fulfil an order, the value of the order (in $10,000), the number of different types of products in the order, and the store location. The data are shown in Table 13-8. (a) Find a simple regr
> Refer to the data in Table 13-9 on diabetic patients and the development of retinopathy. (a) Develop a regression model to predict the probability of development of retinopathy based on years of diabetes and gender of person. Is the model significant at
> Table 13-9 shows data on diabetic patients and the development of retinopathy. The gender of the person, number of years that the person has been diagnosed with diabetes (labelled as Years), and whether the person has developed retinopathy (Y = Yes; N =
> A financial institution is contemplating the offering of three different types of savings accounts. Its elects 100 customers randomly and obtains a response on which account each person would select. What statistical test would you use to determine if cu
> Refer to the data in Table 13-6 on obesity, gender, and occurrence of a heart attack. (a) Develop a regression model to predict the chance of a heart attack based on weight. Interpret the model coefficients. (b) Is the model significant using Î&plu
> Refer to the data in Table 13-8 on order fulfilment time. (a) You believe that there are differences, in general, in the value of orders by location of the store. Consequently, its impact on order fulfilment time may be influenced as such. Find the model
> Refer to the data in Table 13-8 on order fulfilment time. (a) You decide to develop a regression model using order value, number of products, and location of the retailer as predictors. Find the model equation. Is it significant at α =0.05?
> Refer to the data in Table 13-8 on order fulfilment time. (a) You decide to develop a regression model using order value and the number of products in the order as predictors. Find the model equation. Is it significant at α =0.05? (b) Find
> Refer to Exercise 13-9 and the corresponding data shown in Table 13-8. (a) Based on a scatterplot of order fulfillment time versus order value, you decide to fit a quadratic model in order value. What is the model equation? (b) What are values of R2 and
> Refer to Exercise 13-9 and the regression model of time to fulfil an order based on order value. Data from Exercise 13-9: A retail company has information on the time taken (in days) to fulfil an order, the value of the order (in $10,000), the number of
> Consider Exercise 12-50. Four factors (A, B, C, and D), each at three levels, are controlled in an experiment using an L9 orthogonal array. The output quality is classified as acceptable or unacceptable; unacceptable includes both the second-class and re
> In a textile processing plant the quality of the output fabric is believed to be influenced by four factors (A, B, C, and D), each of which can be controlled at three levels. The fabric is classified into three categories: acceptable, second-class, or re
> Consider Exercise 12-48. The design factors are A, B, C, and D, each at three levels. These are assigned to an orthogonal array (inner array) with the factors A, B, C, and D assigned to columns 1, 2, 3, and 4, respectively. Suppose that, in addition to t
> In a food processing plant, four design parameters, A, B, C, and D, each at three levels, have been identified as having an effect on the moisture content in packaged meat. Three noise factors, E, F, and G, each at two levels, are also to be investigated
> Data from a survey of customers are on an ordinal scale (1–7) regarding satisfaction with the services provided in a bank by three tellers. If we wish to determine if the degree of customer satisfaction is independent of the teller, what statistical test
> A travel agency is attempting to enter a market where several competitors currently exist. What are the various customer needs that they should address? How will quality be measured? As the company strives to improve its market share, discuss the impact
> Consider Exercise 12-46. With the assignment of factors, A, B, C, and D to columns 1, 2, 3, and 4, respectively, of an L9 orthogonal array, the output is as follows for another replication of the nine experiments: Determine the main effects. Plot the ave
> In a drilling operation, four factors (A, B, C, and D), each at three levels, are thought to be of importance in influencing the volume of crude oil pumped. Using an L9 orthogonal array, the factors A, B, C, and D are assigned to columns 1, 2, 3, and 4,
> A city library has established three factors (A, B, and C), each at three levels, that influence the satisfaction of their patrons. The library governance committee also believes that the interaction B × C is important. Using an orthogonal array, set up
> The tourism board of a large metropolitan area is seeking ways to promote tourism. They have identified five factors (A, B, C, D, and E) that they feel have an impact on tourist satisfaction. Factor C has four levels, and each of the other four factors h
> A baseball team manager believes that five factors (A, B, C, D, and E), each at two levels, are significant in affecting runs batted in. The manager believes that the interactions B× C and B × E are important. Show an experimental design using an orthogo
> The Environmental Protection Agency has identified four factors (A, B, C, and D), each at two levels, that are significant in their effect on the air pollution level at a photographic film production facility. The agency also feels that the interaction e
> Refer to Exercise 12-40. The restaurant is thinking of hiring more personnel to cut down the service time. However, the additional cost of increasing personnel is estimated to be $0.50 per customer. The results of sampling with the added personnel yield
> A restaurant believes that two of the most important factors that help it attract and retain customers are the price of the item and the time taken to serve the customer. Based on the price for similar items in other neighboring restaurants, it is estima
> Refer to Exercise 12-36. Suppose the manufacturer has the ability to centre the process such that the average thickness of the coating is at 0.005 mm, which is the target value. In doing so, the manufacturer estimates that the standard deviation of the p
> Refer to Exercise 12-36. Suppose that the manufacturer can rework the thickness prior to shipping the product at a cost of $2.00 per reel. What should the manufacturer’s tolerance be? Data from Exercise 12-36: A manufacturer of magnetic tapes is interes
> A county wishes to estimate the average income of people, where it is known that income levels vary quite a bit among the residents in sections of the county. What type of sampling scheme should be used?
> Refer to Exercise 12-36. The manufacturer is considering adopting a new process to reduce the variability in the thickness of coating. It is estimated that the additional cost for this improvement is $0.03 per linear meter. The annual production is 10,00
> A manufacturer of magnetic tapes is interested in reducing the variability of the thickness of the coating on the tape. It is estimated that the loss to the consumer is $10 per reel if the thickness exceeds 0.005 ±0.0004 mm. Each reel has 200 m of tape.
> Refer to Exercise 12-30. Factor A is the concentration of corn extract, factor B is the concentration of an ethylene-based compound, and factor C is the distillation temperature. Each factor will be controlled at two levels. Suppose the experimenter runs
> In a 2^5-2 fractional factorial experiment, using CDE and AB as the generators, find the treatment combinations. Find the aliases of the contrasts.
> Consider a 2^4 factorial experiment. Using BC as the defining contrast, find the treatment combinations in a 2^4–1 fractional factorial experiment. Find the aliases of the contrasts. How would it be possible to estimate the effect of the contrast BC? If
> In Exercise 12-31, use AB as the confounding factor to divide the experiment into two blocks. How would you estimate the effect of factor A? Data from Exercise 12-31: Consider a 2^4 factorial experiment. Set up a table of the coefficients for orthogonal
> Consider a 2^4 factorial experiment. Set up a table of the coefficients for orthogonal contrasts similar to Table 12-25. Write down the contrasts for estimating the main effects and the two-factor interactions. If the four-way interaction effect ABCD is
> In the search for a lower-pollution synthetic fuel, researchers are experimenting with three different factors, each controlled at two levels, for the processing of such a fuel. Factor A is the concentration of corn extract at 5% and 10%, factor B is the
> Write out the treatment combinations for a 2^4 factorial experiment.
> Refer to Exercise 12-20. Consider the following three contrasts: (1) difference between the sum of the reduction in blood sugar levels using diet types 1 and 3 from that using diet types 2 and 4; (2) difference between the sum of the reduction in blood s
> Explain some specific parametric tests that require the distributional assumption of normality. What do you do if the assumption is not satisfied?
> Refer to Exercise 12-19. Consider the following two contrasts of totals: (1) difference between the totals for training programs 1 and 3; (2) difference between the totals for the sum of training programs 1 and 3 and twice that of training program 2. (a)
> Refer to Exercise 12-19. Find a 90% confidence interval for the difference in the mean effectiveness of program 1 and the average of that using programs 2 and 3. Data from Exercise 12-19: Three training programs are being considered for auditors in an a
> Refer to Exercise 12-18. (a) Is there a difference in the mean number of passengers bumped using software packages 1 and 2 from that using software packages 3 and 4? Test at the 10% level of significance. (b) Find a 95% confidence interval for the contra
> Refer to Exercise 12-17. (a) Is there a difference between the mean degree of lateness of company 3 and that of the averages of companies 1 and 2? Test at the 5% level of significance. (b) Find a 90% confidence interval for the contrast defined in part (
> Two controllable factors, temperature and pressure, are each kept at three levels to determine their impact on the ductility of an alloy being produced. The temperature levels are 150, 250, and 300 °C, respectively. Pressure is controlled at 5
> A consulting firm wishes to evaluate the performance of four software packages (A, B, C, and D) as measured by the computational time. The experimenter wishes to control for two variables: the problem type and the operating system configuration used. Fou
> A doctor is contemplating four types of diet to reduce the blood sugar levels of patients. Because of differences in the metabolism of patients, the doctor categorizes the patients into five age groups. From each age group, four patients are selected and
> Three training programs are being considered for auditors in an accounting firm. The success of the training programs is measured on a rating scale from 0 to 100, with higher values indicating a desirable program. The company has categorized its auditors
> An airline is interested in selecting a software package for its reservation system. Even though the company would like to maximize use of its available seats, it prefers to bump as few passengers as possible. It has four software packages to choose from
> A 95% confidence interval for the mean thickness of a part in millimetres is (10.2, 12.9). Interpret this interval.
> A large retail company has to deliver its goods to distributors throughout the country. It has been offered trial-run services by three transportation companies. To test the efficiency of these three companies, it randomly assigns its outgoing product sh
> Refer to Exercise 11-8 concerning the redesigned remote control unit with 25 components in series. If it is desired that the remote unit has a reliability of 0.996 for 3000 hours of operation, what should the failure rate be for each component? What shou
> Refer to Exercise 11-31. Test the null hypothesis of equality of the survival functions of the two groups using a level of significance of 0.05. Data from Exercise 11-31: Two groups of samples of patients were randomly selected from a county. The first
> Two groups of samples of patients were randomly selected from a county. The first group (Group 1) had no history of a chronic disease while the second group (Group 2) had a positive history. The selected patients were observed for a period of 15 years. S
> Refer to Exercise 11-29. If failed items are not replaced during the test, determine the plan using Handbook H-108. Data from Exercise 11-29: In a time-terminated life testing plan, it is desired to reject lots with a mean life of 1500 hours with a prob
> In a time-terminated life testing plan, it is desired to reject lots with a mean life of 1500 hours with a probability of 0.95 and reject lots with a mean life of 7500 hours with a probability of 0.10. The test is to be terminated by 2500 hours. Items th
> Refer to Exercise 11-27. Find the appropriate plan using Handbook H-108 if failed items are not replaced during the test. Data from Exercise 11-27: A time-terminated life testing plan is desired that will accept lots with a mean life of 6000 hours with
> A time-terminated life testing plan is desired that will accept lots with a mean life of 6000 hours with a probability of 0.99 and will accept lots with a mean life of 2000 hours with a probability of 0.10. The test should be terminated by 1200 hours. It
> Refer to Exercise 11-25. If failed items are replaced with similar items, determine a life testing plan using Handbook H-108. Data from Exercise 11-25: A time-terminated life testing plan is to be found that will reject lots that have a mean life of 140
> A time-terminated life testing plan is to be found that will reject lots that have a mean life of 1400 hours with a probability of 0.05. The rejection number is 7, with a sample size of 35. Determine the plan using Handbook H-108 if the time to failure i
> Distinguish between a hypergeometric and a binomial random variable.
> Refer to Exercise 11-23. Suppose that items that fail during the test are immediately replaced with similar items. Determine the life testing plan using Handbook H-108. Data from Exercise 11-23: A time-terminated life testing plan is to be found that wi
> A time-terminated life testing plan is to be found that will reject lots with a mean life of 1500 hours with a probability 0.05 and accept lots with a mean life of 600 hours with a probability of 0.10. Items that fail during the test are not replaced. De
> A life testing plan is to be terminated after the third failure. It should accept a lot that has an acceptable mean life of 600 hours with a probability of 0.99. Failed items are not replaced during the test. A sample of eight items is chosen, and three
> Refer to Exercise 11-20. Assume that failed items are immediately replaced during the test. Using Handbook H-108, what is your recommendation on the lot? Data from Exercise 11-20: A life testing plan is to be terminated after the eighth failure. It shou
> A life testing plan isto be terminated after the eighth failure. It should reject a lot that has an acceptable mean life of 900 hours with a probability of 0.10. Items that fail during the test are not replaced. A sample of 15 items is placed on test wit
> A sample of 25 relays is chosen for life testing. The time to failure of a relay is exponentially distributed. The test is terminated after 800 hours, with five failures being observed at times 610, 630, 680, 700, and 720 hours. Failed items are not repl
> Refer to Exercise 11-17. Assume that each failed item is replaced with an identical unit. Estimate the mean time to failure and the failure rate. Find a 90% confidence interval for the mean time to failure. Data from Exercise 11-17: A sample of 20 diode
> A sample of 20 diodes is chosen for life testing. The time to failure of the diodes is exponentially distributed. The test is terminated after six failures, with no replacement of the failed items. The failure times (in hours) of the six diodes are 530,
> Construct the OC curve for the life testing plan n= 6, T =900 hours, c =3. For a producer’s risk of 0.05, what is the associated quality of batches as indicated by their mean life? For a consumer’s risk of 0.10, what is the associated quality level of ba
> Refer to Exercise 11-13 and the system shown in Figure 11-14. Suppose that component B is a standby component. Find the reliability of the system after 1000 hours. What is the mean time to failure? Data from Exercise 11-13: Consider the seven-component
> State the null and alternative hypotheses in the following situations by defining the parameters used. Also, state any assumptions that you need to make to conduct the test: (a) The Postal Service wishes to prove that the mean delivery time for packages
> A standby system has a basic unit with four standby components. The time to failure of each component has an exponential distribution with a failure rate of 0.008/hour. For a 400-hour operation period, find the reliability of the standby system. What is
> Consider the seven-component system shown in Figure 11-14. Assume that the time to failure for each component has an exponential distribution. The failure rates are as follows: λA = 0.0005/hour, λB= 0.0005/hour, λC=
> Consider the seven-component system shown in Figure 11-14. The reliabilities of the components are as follows: RA = 0.96, RB= 0.92, RC=0.94, RD = 0.89, RE = 0.95, RF=0.88, RG =0.90. Find the reliability of the system. If you had a choice of improving sys
> Refer to Exercise 11-10. Each component has a time to failure that is exponentially distributed, with a mean time to failure of 3000 hours. Find the reliability of the subassembly for 2500 hours of operation. What is the mean time to failure of the subas
> Four components A, B, C, and D are placed in parallel to make a subassembly in a circuit board. The reliabilities of A, B, C, and D are 0.93, 0.88, 0.95, and 0.92, respectively. Find the reliability of the subassembly.
> A cereal manufacturer who claims to meet certain mineral and vitamin requirements has a minimum specification of 25% for the iron content. The standard deviation of the iron content is estimated to be 3%. It is preferred to accept batches that are 1.5% n
> The thickness of silicon wafers is an important characteristic in microelectronic circuits. The upper specification limit for the thickness is 0.015 mm. It is estimated that the standard deviation of the thickness of wafers is 0. 0014mm.We wish to accept
> A dairy has to control the amount of butterfat in its low-fat milk. The upper specification limit of the fat content is 4 g for 4-L containers. The standard deviation of the fat content for these containers is estimated to be 0.5 g. It is desired to acce
> Unleaded gasoline must meet certain federal standards. The octane number for a particular brand must be at least 89. The standard deviation of the octane number is estimated to be 4. It is preferred to accept shipments for which the average octane number
> Refer to Exercise 10-52 regarding the proportion of carbon monoxide in exhaust gases, which has an upper specification limit of 0.30. Ifthe average carbon monoxide content is 1 standard deviation below the upper specification limit, the devices should be
> Distinguish between the use of the mean, median, and mode in quality control applications. When do you prefer to use the trimmed mean?
> The proportion of carbon monoxide in exhaust gases has an upper specification limit of 0.30. Emission control devices are being tested to meet such requirements. We wish that devices with an average carbon monoxide content of 0.15 or less be accepted 95%
> The length of connector pins has an upper specification limit of 45 mm and a lower specification limit of 40 mm. It is desirable that lots with a mean such that 8% of the product is nonconforming, either above the upper specification limit or below the l
> The tensile strength of an alloy has double specification limits. If the process average tensile strength is below 800 kg/cm2 or above 1200 kg/cm2, it is desired to accept such lots with a probability of 0.08. For lots with a process average of 1000 kg/c
> The lower specification limit for the breaking strength of yarns is 25 g. The distribution of the breaking strength of yarns is normal with a variance of 6. It is desirable that lots with a mean such that 3% of the product is nonconforming be accepted 94
> The upper specification limit for the resistance of coils is 30 Ω. The distribution of coil resistance is known to be normal with a standard deviation of 5 Ω. It is preferred to reject batches that have a mean of 2.3 standard deviations below the upper s
> In the construction industry, the initial inspection of tie beams is estimated to cost $0.20 per unit. If, however, a nonconforming beam is allowed for construction purposes, the unit cost of rectifying and replacing it is $50. What inspection policy sho
> Refer to Exercise 10-44. lf the monthly production is 2000 units, what is the average savings in total inspection costs when using Deming’s kp rule as opposed to 100% inspection? Data from Exercise 10-44: In Exercise 10-43, if the initial inspection cos
> Refer to Exercise 10-43, Suppose that the monthly production is 3000 units. What is the average savings in total inspection costs per month when using the policy found from Deming’s kp rule as opposed to no inspection? Data from Exercise 10-43: The init
> In Exercise 10-43, if the initial inspection costs of the transmission systems are $1.00 per unit, what inspection policy should be followed using Deming’s kp rule? Data from Exercise 10-43: The initial inspection of transmission systems in automobiles
> The initial inspection of transmission systems in automobiles is estimated to cost $0.50 per unit. If a nonconforming transmission is allowed in the assembly, the unit cost to eventually disassemble and replace it is $225. The estimated proportion noncon
> Explain the different types of measurement scales and give examples in the following situations: (a) Gallons of water to put out a fire by the fire department (b) Response time of an ambulance (c) Test score in an examination (d) Customer product prefere
> A sequential sampling plan is to be used. It is desirable to have a producer’s risk of 0.05 at AQL= 0.008 and a consumer’s risk of 0.07 at LQL= 0.082. Determine the equations for the acceptance and rejection lines. What is the first opportunity to reject

