Question: Construct the indicated confidence interval for µd.
Construct the indicated confidence interval for µd. Assume the populations are normally distributed.
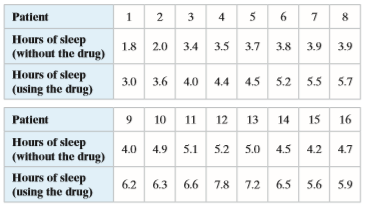
A sleep disorder specialist wants to test the effectiveness of a new drug that is reported to increase the number of hours of sleep patients get during the night. To do so, the specialist randomly selects 16 patients and records the number of hours of sleep each gets with and without the new drug. The table shows the results of the two-night study. Construct a 90% confidence interval for µd.
Transcribed Image Text:
Patient 1 3 4 5 6 7 8 Hours of sleep (without the drug) 1.8 2.0 3.4 3.5 3.7 3.8 3.9 3.9 Hours of sleep (using the drug) 3.0 3.6 4.0 4.4 4.5 5.2 5.5 5.7 Patient 10 11 12 13 14 15 16 Hours of sleep (without the drug) 4.0 4.9 5.1 5.2 5.0 4.5 4.2 4.7 Hours of sleep (using the drug) 6.2 6.3 6.6 7.8 7.2 6.5 5.6 5.9 2.
> Two variables are given that have been shown to have correlation but no cause-and-effect relationship. Describe at least one possible reason for the correlation. Value of home and life span
> The scatter plots show the results of a survey of 20 randomly selected males ages 24–35. Using age as the explanatory variable, match each graph with the appropriate description. Explain your reasoning. a. Age and body temperature b. A
> The scatter plots show the results of a survey of 20 randomly selected males ages 24–35. Using age as the explanatory variable, match each graph with the appropriate description. Explain your reasoning. a. Age and body temperature b. A
> The scatter plots show the results of a survey of 20 randomly selected males ages 24–35. Using age as the explanatory variable, match each graph with the appropriate description. Explain your reasoning. a. Age and body temperature b. A
> The scatter plots show the results of a survey of 20 randomly selected males ages 24–35. Using age as the explanatory variable, match each graph with the appropriate description. Explain your reasoning. a. Age and body temperature b. A
> Identify the explanatory variable and the response variable. An actuary at an insurance company wants to determine whether the number of hours of safety driving classes can be used to predict the number of driving accidents for each driver.
> Identify the explanatory variable and the response variable. A nutritionist wants to determine whether the amounts of water consumed each day by persons of the same weight and on the same diet can be used to predict individual weight loss.
> Determine whether there is a perfect positive linear correlation, a strong positive linear correlation, a perfect negative linear correlation, a strong negative linear correlation, or no linear correlation between the variables.
> The table at the right shows the residential natural gas expenditures (in dollars) in one year for a random sample of households in four regions of the United States. Assume that the populations are normally distributed and the population variances are e
> a. Identify the claim and state H0 and Ha. b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test, a t-test, or a chi-square test. Explain your reasoning. c. Choose one of the options. Option
> Determine whether there is a perfect positive linear correlation, a strong positive linear correlation, a perfect negative linear correlation, a strong negative linear correlation, or no linear correlation between the variables.
> Determine whether there is a perfect positive linear correlation, a strong positive linear correlation, a perfect negative linear correlation, a strong negative linear correlation, or no linear correlation between the variables.
> Two variables have a positive linear correlation. Does the dependent variable increase or decrease as the independent variable increases? What if the variables have a negative linear correlation?
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> Determine whether a normal sampling distribution can be used. If it can be used, test the claim about the difference between two population proportions p1 and p2 at the level of significance a. Assume the samples are random and independent. Claim: p1 > p
> Determine whether a normal sampling distribution can be used. If it can be used, test the claim about the difference between two population proportions p1 and p2 at the level of significance a. Assume the samples are random and independent. Claim: p1 = p
> Determine whether a normal sampling distribution can be used. If it can be used, test the claim about the difference between two population proportions p1 and p2 at the level of significance a. Assume the samples are random and independent. Claim: p1 < p
> Determine whether a normal sampling distribution can be used. If it can be used, test the claim about the difference between two population proportions p1 and p2 at the level of significance a. Assume the samples are random and independent. Claim: p1 ≠ p
> The table below shows the winning times (in seconds) for the men’s and women’s 100-meter runs in the Summer Olympics from 1928 to 2016. a. Display the data in a scatter plot, calculate the correlation coefficient r, a
> Construct the indicated confidence interval for p1 - p2. Assume the samples are random and independent. Repeat Exercise 25 but with a 99% confidence interval. Compare your result with the result in Section 6.3, Exercise 27, part (b).
> Construct the indicated confidence interval for p1 - p2. Assume the samples are random and independent. In Section 6.3, Exercises 27 and 28, let p1 be the proportion of the population of U.S. college graduates who expect to stay at their first employer f
> Construct the indicated confidence interval for p1 - p2. Assume the samples are random and independent. In a survey of 10,000 students taking the SAT, 7% were undecided on an intended college major. In another survey of 8000 students taken 10 years befor
> Construct the indicated confidence interval for p1 - p2. Assume the samples are random and independent. In a survey of 10,000 students taking the SAT, 7% were planning to study visual and performing arts in college. In another survey of 8000 students tak
> Use the figure shown at the left, which gives the percentages of full-time employed men and women in the United States who work 40 hours per week and who work more than 40 hours per week. Assume the survey included random samples of 300 men and 250 women
> Use the figure shown at the left, which gives the percentages of full-time employed men and women in the United States who work 40 hours per week and who work more than 40 hours per week. Assume the survey included random samples of 300 men and 250 women
> Use the figure shown at the left, which gives the percentages of full-time employed men and women in the United States who work 40 hours per week and who work more than 40 hours per week. Assume the survey included random samples of 300 men and 250 women
> Explain how to perform a two-sample z-test for the difference between two population proportions.
> Use the figure shown at the left, which gives the percentages of full-time employed men and women in the United States who work 40 hours per week and who work more than 40 hours per week. Assume the survey included random samples of 300 men and 250 women
> Use the figure, which shows the percentages of newlyweds in the United States who have a spouse of a different race or ethnicity. The survey included random samples of 1000 Asian newlyweds, 1000Â Hispanic newlyweds, 1000 black newlyweds, and 1
> Use the figure, which shows the percentages of newlyweds in the United States who have a spouse of a different race or ethnicity. The survey included random samples of 1000 Asian newlyweds, 1000Â Hispanic newlyweds, 1000 black newlyweds, and 1
> Use the figure, which shows the percentages of newlyweds in the United States who have a spouse of a different race or ethnicity. The survey included random samples of 1000 Asian newlyweds, 1000Â Hispanic newlyweds, 1000 black newlyweds, and 1
> Use the figure, which shows the percentages of newlyweds in the United States who have a spouse of a different race or ethnicity. The survey included random samples of 1000 Asian newlyweds, 1000Â Hispanic newlyweds, 1000 black newlyweds, and 1
> Use the figure, which shows the percentages of newlyweds in the United States who have a spouse of a different race or ethnicity. The survey included random samples of 1000 Asian newlyweds, 1000Â Hispanic newlyweds, 1000 black newlyweds, and 1
> Use the figure, which shows the percentages of newlyweds in the United States who have a spouse of a different race or ethnicity. The survey included random samples of 1000 Asian newlyweds, 1000Â Hispanic newlyweds, 1000 black newlyweds, and 1
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> What conditions are necessary in order to use the z-test to test the difference between two population proportions?
> The contingency table shows how a random sample of adults rated a newly released movie and gender. At α = 0.05, can you conclude that the adults’ ratings are related to gender? Rating Gender Excellent Good Fair Роor Ma
> Test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed. Claim: µd ≠ 0; α = 0.10. Sample statistics: d = -1
> Test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed. Claim: µd ≥ 0; α = 0.01. Sample statistics: d = -2
> Test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed. Claim: µd > 0; α = 0.05. Sample statistics: d = 0.
> Test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed. Claim: µd ≤ 0; α = 0.10. Sample statistics: d = 6.
> Test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed. Claim: µd = 0; α = 0.01. Sample statistics: d = 3.
> Test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed. Claim: µd < 0; α = 0.05. Sample statistics: d = 1.
> Construct the indicated confidence interval for µd. Assume the populations are normally distributed. A sleep disorder specialist wants to test whether herbal medicine increases the number of hours of sleep patients get during the night. To d
> In Exercise 18, use technology to perform the hypothesis test with a P-value. Compare your result with the result obtained using rejection regions. Are they the same? From Exercise 18: Assume the samples are random and dependent, and the populations are
> In Exercise 15, use technology to perform the hypothesis test with a P-value. Compare your result with the result obtained using rejection regions. Are they the same? From Exercise 15: Assume the samples are random and dependent, and the populations are
> A researcher claims that the credit card debts of college students are distributed as shown in the pie chart. You randomly select 900 college students and record the credit card debt of each. The table shows the results. At α = 0.05, test
> Explain what the symbols d and sd represent.
> A school administrator claims that the standard deviations of reading test scores for eighth-grade students are the same in Colorado and Utah. A random sample of 16 test scores from Colorado has a standard deviation of 34.6 points, and a random sample of
> What conditions are necessary in order to use the dependent samples t-test for the mean of the differences for a population of paired data?
> Test the claim about the difference between two population means µ1 and µ2 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: µ1 = µ2; α = 0.01. Assume σ12 = σ22 Sample sta
> Use Table 5 in Appendix B to find the critical value(s) for the alternative hypothesis, level of significance α, and sample sizes n1 and n2. Assume that the samples are random and independent, the populations are normally distributed, and t
> Use Table 5 in Appendix B to find the critical value(s) for the alternative hypothesis, level of significance α, and sample sizes n1 and n2. Assume that the samples are random and independent, the populations are normally distributed, and t
> Use Table 5 in Appendix B to find the critical value(s) for the alternative hypothesis, level of significance α, and sample sizes n1 and n2. Assume that the samples are random and independent, the populations are normally distributed, and t
> Use Table 5 in Appendix B to find the critical value(s) for the alternative hypothesis, level of significance α, and sample sizes n1 and n2. Assume that the samples are random and independent, the populations are normally distributed, and t
> Use Table 5 in Appendix B to find the critical value(s) for the alternative hypothesis, level of significance α, and sample sizes n1 and n2. Assume that the samples are random and independent, the populations are normally distributed, and t
> Use Table 5 in Appendix B to find the critical value(s) for the alternative hypothesis, level of significance α, and sample sizes n1 and n2. Assume that the samples are random and independent, the populations are normally distributed, and t
> Construct the indicated confidence interval for µ1 - µ2. Assume the populations are approximately normal with equal variances. To compare the mean ages of male and female participants in a 10K race, you randomly select several a
> Construct the indicated confidence interval for µ1 - µ2. Assume the populations are approximately normal with equal variances. To compare the mean number of days spent waiting to see a family doctor for two large cities, you ran
> Construct the indicated confidence interval for µ1 - µ2. Assume the populations are approximately normal with unequal variances. To compare the mean driving distances for two golfers, you randomly select several drives from each
> Construct the indicated confidence interval for µ1 - µ2. Assume the populations are approximately normal with unequal variances. To compare the mean finishing times of male and female participants in a 10K race, you randomly sel
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret
> Explain how to perform a two-sample t-test for the difference between two population means.
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> Construct the indicated confidence interval for the population mean µ. Which distribution did you use to create the confidence interval? c = 0.90, x = 8.21, σ = 0.62, n = 8
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret
> Test the claim about the difference between two population means µ1 and µ2 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: µ1 > µ2; α = 0.01. Assume σ12 ≠ σ22 Sample sta
> Test the claim about the difference between two population means µ1 and µ2 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: µ1 ≤ µ2; α = 0.05. Assume σ12 ≠ σ22 Sample sta
> Test the claim about the difference between two population means µ1 and µ2 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: µ1 < µ2; α = 0.10. Assume σ12 = σ22 Sample sta
> What conditions are necessary in order to use the t-test to test the difference between two population means?
> Use the TI-84 Plus display to make a decision to reject or fail to reject the null hypothesis at the level of significance. Make your decision using the standardized test statistic and using the P-value. Assume the sample sizes are equal. &Ic
> Construct the indicated confidence interval for the population mean µ. Which distribution did you use to create the confidence interval? c = 0.99, x = 12.1, s = 2.64, n = 26
> Classify the two samples as independent or dependent and justify your answer. Sample 1: The commute times of 10 workers when they use their own vehicles Sample 2: The commute times of the same 10 workers when they use public transportation
> Classify the two samples as independent or dependent and justify your answer. Sample 1: The average speed of 23 powerboats using an old hull design Sample 2: The average speed of 14 powerboats using a new hull design
> Classify the two samples as independent or dependent and justify your answer. Sample 1: The IQ scores of 60 females Sample 2: The IQ scores of 60 males
> Classify the two samples as independent or dependent and justify your answer. Sample 1: The maximum bench press weights for 53 football players Sample 2: The maximum bench press weights for the same 53 football players after completing a weight liftin
> What conditions are necessary in order to use the z-test to test the difference between two population means?
> Construct the indicated confidence interval for µ1 - µ2. Construct a 99% confidence interval for the difference between the mean annual salaries of entry level architects in Denver, Colorado, and Los Angeles, California, using t
> Describe another way you can perform a hypothesis test for the difference between the means of two populations using independent samples with σ1 and σ2 known that does not use rejection regions.
> Construct the indicated confidence interval for µ1 - µ2. Construct a 95% confidence interval for the difference between the mean annual salaries of entry level software engineers in Raleigh, North Carolina, and Wichita, Kansas,
> Is the difference between the mean annual salaries of entry level architects in Denver, Colorado, and Los Angeles, California, equal to $10,000? To decide, you select a random sample of entry level architects from each city. The results of each survey ar
> Is the difference between the mean annual salaries of entry level software engineers in Raleigh, North Carolina, and Wichita, Kansas, more than $2000? To decide, you select a random sample of entry level software engineers from each city. The results of
> Construct the indicated confidence interval for the population mean µ. Which distribution did you use to create the confidence interval? c = 0.95, x = 3.46, s = 1.63, n = 16
> Explain why the null hypothesis H0: µ1 ≥ µ2 is equivalent to the null hypothesis H0: µ1 - µ2 ≥ 0.
> Explain why the null hypothesis H0: µ1 = µ2 is equivalent to the null hypothesis H0: µ1 - µ2 = 0.
> a. identify the claim and state H0, and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decisio
> a. identify the claim and state H0, and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decisio
> a. identify the claim and state H0, and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decisio
> a. identify the claim and state H0, and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decisio

