Question: Decide which of the curves in Fig.
Decide which of the curves in Fig. 24 could not be the graph of f (x) = (3x2 + 1)4 for x ≥ 0. Decide which of the curves in Fig. 24 could not be the graph of f (x) = (3x2 + 1)4 for x ≥ 0 by considering the derivative of f (x). Explain your answer.
Figure 24:
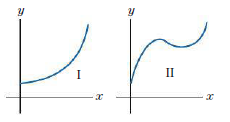
Transcribed Image Text:
fi I Y II
> The graph of function has one relative extreme point. Find it (giving both x- and y-coordinates) and determine if it is a relative maximum or a relative minimum point. Do not include a sketch of the graph of the function. f (x) = 1/4 x2 - 2x + 7
> Let a, b, c, d be fixed numbers with a ≠ 0, and let f (x) = ax3 + bx2 + cx + d. Is it possible for the graph of f (x) to have more than one inflection point? Explain your answer.
> Differentiate. f (x) = (√x/2 + 1)3/2
> Let a, b, c be fixed numbers with a ≠ 0, and let f (x) = ax2 + bx + c. Is it possible for the graph of f (x) to have an inflection point? Explain your answer.
> Sketch the following curves, indicating all relative extreme points and inflection points. y = x4 – 4/3 x3
> Sketch the following curves, indicating all relative extreme points and inflection points. y = 2x3 - 3x2 - 36x + 20
> Sketch the following curves, indicating all relative extreme points and inflection points. y = x4 + 1/3 x3 - 2x2 - x + 1
> Sketch the following curves, indicating all relative extreme points and inflection points. y = 1/3 x3 - x2 - 3x + 5
> Sketch the following curves, indicating all relative extreme points and inflection points. y = -x3 + 12x - 4
> Sketch the following curves, indicating all relative extreme points and inflection points. y = 1 + 3x2 - x3
> Sketch the following curves, indicating all relative extreme points and inflection points. y = x3 - 6x2 + 9x + 3
> Sketch the following curves, indicating all relative extreme points and inflection points. y = x3 - 3x + 2
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. ƒ(x) = {x³ + 2x² − 5x +
> Differentiate. y = π2x
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. f(x) = −x³ + 2x² - 12
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. 3 f(x) = 2x³ − 15x² + 36x - 24
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. 3 f(x) = -√√x³ + x² + 9x
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. f(x) = x³ + 9x - 2
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. f(x) = x³ - 12x
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. f(x) = x³ = x²
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. f (x) = x3 + 6x2 + 9x
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> Differentiate. y = x + 1 + √(x + 1)
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = 2x3 + 3x2 - 3 Critical Values Inte
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = -x3 - 12x2 - 2 Critical Values Int
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = 4/3 x3 - x + 2 Critical Values Int
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = 1/3 x3 – x2 + 1
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = -6x3 – 3/2 x2 + 3x -
> Differentiate. y = (1 + x + x2)11
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = -x3 + 6x2 - 9x + 1 Critical Values
> Refer to the functions whose graphs are given in Fig. 17. Figure 17: Which functions have a negative second derivative for all x? Y Y (a) (d) Figure 17 Y Y (b) (e) Y Y (c) (f)
> Refer to the functions whose graphs are given in Fig. 17. Figure 17: Which functions have a positive second derivative for all x? Y Y (a) (d) Figure 17 Y Y (b) (e) Y Y (c) (f)
> Refer to the functions whose graphs are given in Fig. 17. Figure 17: Which functions have a negative first derivative for all x? Y Y (a) (d) Figure 17 Y Y (b) (e) Y Y (c) (f)
> Refer to the functions whose graphs are given in Fig. 17. Figure 17: Which functions have a positive first derivative for all x?
> Display the graph of the derivative of f (x) in the specified window. Then use the graph of f (x) to determine the approximate values of x at which the graph of f (x) has relative extreme points and inflection points. Then check your conclusions by disp
> Display the graph of the derivative of f (x) in the specified window. Then use the graph of f (x) to determine the approximate values of x at which the graph of f (x) has relative extreme points and inflection points. Then check your conclusions by disp
> After a drug is taken orally, the amount of the drug in the bloodstream after t hours is f (t) units. Figure 27 shows partial graphs of f ‘(t) and f ’’(t). Figure 27: (a) Is the amount of the drug
> The number of farms in the United States t years after 1925 is f (t) million, where f is the function graphed in Fig. 26(a). [The graphs of f ‘(t) and f ’’(t) are shown in Fig. 26(b).] Figure 26: (
> Match each observation (a)–(e) with a conclusion (A)–(E). Observations (a) The point (3, 4) is on the graph of f ‘(x). (b) The point (3, 4) is on the graph of f (x). (c) The point (3, 4) is on the graph of f ’’(x). (d) The point (3, 0) is on the graph of
> Differentiate. y = 45 / (1 + x + √x)
> By looking at the second derivative, decide which of the curves in Fig. 25 could be the graph of f (x) = x5/2. Figure 25: fi x Y II
> By looking at the first derivative, decide which of the curves in Fig. 24 could not be the graph of f (x) = x3 - 9x2 + 24x + 1 for x ≥ 0. Figure 24: fi I Y II
> T (t) is the temperature on a hot summer day at time t hours. (a) If T’(10) = 4, by approximately how much will the temperature rise from 10:00 to 10:45? (b) Which of the following two conditions is the better news if you do not like hot weather? Explain
> Melting snow causes a river to overflow its banks. Let h (t) denote the number of inches of water on Main Street t hours after the melting begins. (a) If h’(100) = 13, by approximately how much will the water level change during the next half hour? (b) W
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: If f (0) = 3, what is the equation of the tangent line to the graph of y = f (x) at x = 0? 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: If f (0) = 3, what is an approximate value of f (.25)? 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: If f (6) = 8, what is an approximate value of f (6.5)? 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: If f (6) = 3, what is the equation of the tangent line to the graph of y = f (x) at x = 6? 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) has an inflection point at x = 4. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Differentiate. y = 7 / √(1 + x)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) has an inflection point at x = 1. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) must be concave down at x = 2. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) must be concave up at x = 0. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) has a relative minimum at x = 5. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) has a relative maximum at x = 3. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) must be decreasing at x = 4. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) must be increasing at x = 6. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> In Fig. 22, the t-axis represents time in minutes. Figure 22: (a) What is f (2)? (b) Solve f (t) = 1. (c) When does f (t) attain its greatest value? (d) When does f (t) attain its least value? (e) What is the rate of change of f (t) at t = 7.5? (f ) W
> Refer to Fig. 21. Figure 21: (a) Looking at the graph of f ‘(x), determine whether f (x) is increasing or decreasing at x = 9. Look at the graph of f (x) to confirm your answer. (b) Looking at the values of f ‘(x) f
> Suppose that Fig. 20 contains the graph of y = Ï… (t), the velo city of a car after t hours. Is the car going faster at t = 1 or t = 2? Figure 20: Figure 20 y 1 2
> Differentiate. y = 2 / 1 - 5x
> Suppose that Fig. 20 contains the graph of y = s (t), the distance traveled by a car after t hours. Is the car going faster at t = 1 or t = 2? Figure 20: Figure 20 y 1 2
> The first and second derivatives of the function f (x) have the values given in Table 1. (a) Find the x-coordinates of all relative extreme points. (b) Find the x-coordinates of all inflection points. Table 1: Table 1 Values of the First Two Deriva
> Refer to the graph in Fig. 19. Fill in each box of the grid with either POS, NEG, or 0. Figure 19: Y Figure 19 y = f(x) B x A B C f'
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = 3, f ‘(3) = 1, inflection point at x = 3, f ’’(x) < 0 for x > 3
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = -2, f ‘(3) = 2, f ’’(3) = 3
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = 4, f (3) = - 3/2 , f (3) = -2
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = 1, f ‘(3) = 0, inflection point at x = 3, f ‘(x) > 0 for x > 3
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = -2, f ‘(3) = 0, f ’’(3) = 1
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = 4, f ‘(3) = - 1/2, f ’’(3) = 5
> Sketch the graph of a function that has the properties described. f (x) defined only for x ≥ 0; (0, 0) and (5, 6) are on the graph; f ‘(x) > 0 for x ≥ 0; f ’’(x) < 0 for x < 5, f ’’(5) = 0, f ’’(x) > 0 for x > 5.
> Differentiate. y = 1 / 2x + 5
> Differentiate. y = 3√3 x
> Sketch the graph of a function that has the properties described. (0, 6), (2, 3), and (4, 0) are on the graph; f ‘(0) = 0 and f ‘(4) = 0; f ’’(x) < 0 for x < 2, f ’’(2) = 0, f ’’(x) > 0 for x > 2.
> Sketch the graph of a function that has the properties described. (-2, -1) and (2, 5) are on the graph; f ‘(-2) = 0 and f ‘(2) = 0; f ’’(x) > 0 for x < 0, f ’’(0) = 0, f ’’(x) < 0 for x > 0.
> Sketch the graph of a function that has the properties described. f (3) = 5; f (x) > 0 for x < 3, f ‘(3) = 0 and f (x) > 0 for x > 3.
> Sketch the graph of a function that has the properties described. f (-1) = 0; f ‘(x) 6 0 for x < -1, f ‘(-1) = 0 and f ‘(x) > 0 for x > -1.
> Sketch the graph of a function that has the properties described. f (2) = 1; f ‘(2) = 0; concave up for all x.
> Which one of the graphs in Fig. 18 could represent a function f (x) for which f (a) = 0, f ‘(a) 0? Figure 18: y Y Figure 18 a (a) a (c) y Y a (b) a (d) 8
> Which one of the graphs in Fig. 18 could represent a function f (x) for which f (a) > 0, f ‘(a) = 0, and f ’’(a) Figure 18: y Y Figure 18 a (a) a (c) y Y a (b) a (d) 8
> Describe the following graph. THE + Y
> Describe the following graph. 引
> Refer to graphs (a)–(f) in Fig. 19. Figure 19: Which functions have the property that the slope always decreases as x increases? K (a) (c) (e) n Figure 19 (b) 44 Y ㅅ (d) 1 (f) x 2
> Differentiate. y = √(1 + x + x2)
> Refer to graphs (a)–(f) in Fig. 19. Figure 19: Which functions have the property that the slope always increases as x increases? K (a) (c) (e) n Figure 19 (b) 44 Y ㅅ (d) 1 (f) x 2
> Refer to graphs (a)–(f) in Fig. 19. Figure 19: Which functions are decreasing for all x? K (a) (c) (e) n Figure 19 (b) 44 Y ㅅ (d) 1 (f) x 2
> Refer to graphs (a)–(f) in Fig. 19. Figure 19: Which functions are increasing for all x? K (a) (c) (e) n Figure 19 (b) 44 Y ㅅ (d) 1 (f) x 2
> Simultaneously graph the functions y = 1/x + x and y = x in the window [-6, 6] by [-6, 6]. Describe the asymptote of the first function.
> The graph of the function f (x) = 2x2 – 1 / .5x2 + 6 has a horizontal asymptote of the form y = c. Estimate the value of c by graphing f (x) in the window [0, 50] by [-1, 6].
> Graph the function f (x) = 1 / x3 - 2x2 + x - 2 in the window [0, 4] by [-15, 15]. For what value of x does f (x) have a vertical asymptote?
> If the function f (x) has a relative minimum at x = a and a relative maximum at x = b, must f (a) be less than f (b)?
> Consider a smooth curve with no undefined points. (a) If it has two relative maximum points, must it have a relative minimum point? (b) If it has two relative extreme points, must it have an inflection point?
> Sketch the graph of a function having the given properties. Defined for x ≥ 0; absolute minimum value at x = 0; relative maximum point at x = 4; asymptotic to the line y = (x/2) + 1

