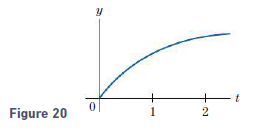
Question: Suppose that Fig. 20 contains the graph
Suppose that Fig. 20 contains the graph of y = Ï… (t), the velo city of a car after t hours. Is the car going faster at t = 1 or t = 2?
Figure 20:
Transcribed Image Text:
Figure 20 y 1 2
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. f(x) = x³ - 12x
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. f(x) = x³ = x²
> The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. f (x) = x3 + 6x2 + 9x
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> Differentiate. y = x + 1 + √(x + 1)
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. [Recall that if f (x) = ax2 + bx + c, then f (x) has a relative minimum point when a > 0 and a relativ
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = 2x3 + 3x2 - 3 Critical Values Inte
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = -x3 - 12x2 - 2 Critical Values Int
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = 4/3 x3 - x + 2 Critical Values Int
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = 1/3 x3 – x2 + 1
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = -6x3 – 3/2 x2 + 3x -
> Differentiate. y = (1 + x + x2)11
> The graph of the function has one relative maximum and one relative minimum point. Find these points using the first-derivative test. Use a variation chart as in Example 1. Variation Chart from Example 1: f (x) = -x3 + 6x2 - 9x + 1 Critical Values
> Refer to the functions whose graphs are given in Fig. 17. Figure 17: Which functions have a negative second derivative for all x? Y Y (a) (d) Figure 17 Y Y (b) (e) Y Y (c) (f)
> Refer to the functions whose graphs are given in Fig. 17. Figure 17: Which functions have a positive second derivative for all x? Y Y (a) (d) Figure 17 Y Y (b) (e) Y Y (c) (f)
> Refer to the functions whose graphs are given in Fig. 17. Figure 17: Which functions have a negative first derivative for all x? Y Y (a) (d) Figure 17 Y Y (b) (e) Y Y (c) (f)
> Refer to the functions whose graphs are given in Fig. 17. Figure 17: Which functions have a positive first derivative for all x?
> Display the graph of the derivative of f (x) in the specified window. Then use the graph of f (x) to determine the approximate values of x at which the graph of f (x) has relative extreme points and inflection points. Then check your conclusions by disp
> Display the graph of the derivative of f (x) in the specified window. Then use the graph of f (x) to determine the approximate values of x at which the graph of f (x) has relative extreme points and inflection points. Then check your conclusions by disp
> After a drug is taken orally, the amount of the drug in the bloodstream after t hours is f (t) units. Figure 27 shows partial graphs of f ‘(t) and f ’’(t). Figure 27: (a) Is the amount of the drug
> The number of farms in the United States t years after 1925 is f (t) million, where f is the function graphed in Fig. 26(a). [The graphs of f ‘(t) and f ’’(t) are shown in Fig. 26(b).] Figure 26: (
> Match each observation (a)–(e) with a conclusion (A)–(E). Observations (a) The point (3, 4) is on the graph of f ‘(x). (b) The point (3, 4) is on the graph of f (x). (c) The point (3, 4) is on the graph of f ’’(x). (d) The point (3, 0) is on the graph of
> Differentiate. y = 45 / (1 + x + √x)
> By looking at the second derivative, decide which of the curves in Fig. 25 could be the graph of f (x) = x5/2. Figure 25: fi x Y II
> By looking at the first derivative, decide which of the curves in Fig. 24 could not be the graph of f (x) = x3 - 9x2 + 24x + 1 for x ≥ 0. Figure 24: fi I Y II
> Decide which of the curves in Fig. 24 could not be the graph of f (x) = (3x2 + 1)4 for x ≥ 0. Decide which of the curves in Fig. 24 could not be the graph of f (x) = (3x2 + 1)4 for x ≥ 0 by considering the derivative of
> T (t) is the temperature on a hot summer day at time t hours. (a) If T’(10) = 4, by approximately how much will the temperature rise from 10:00 to 10:45? (b) Which of the following two conditions is the better news if you do not like hot weather? Explain
> Melting snow causes a river to overflow its banks. Let h (t) denote the number of inches of water on Main Street t hours after the melting begins. (a) If h’(100) = 13, by approximately how much will the water level change during the next half hour? (b) W
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: If f (0) = 3, what is the equation of the tangent line to the graph of y = f (x) at x = 0? 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: If f (0) = 3, what is an approximate value of f (.25)? 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: If f (6) = 8, what is an approximate value of f (6.5)? 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: If f (6) = 3, what is the equation of the tangent line to the graph of y = f (x) at x = 6? 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) has an inflection point at x = 4. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Differentiate. y = 7 / √(1 + x)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) has an inflection point at x = 1. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) must be concave down at x = 2. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) must be concave up at x = 0. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) has a relative minimum at x = 5. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) has a relative maximum at x = 3. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) must be decreasing at x = 4. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> Refer to Fig. 23, which contains the graph of f ‘(x), the derivative of the function f (x). Figure 23: Explain why f (x) must be increasing at x = 6. 3 CO 2 1 -2 y y = f'(x) 1 2 3 5 6 (6,2)
> In Fig. 22, the t-axis represents time in minutes. Figure 22: (a) What is f (2)? (b) Solve f (t) = 1. (c) When does f (t) attain its greatest value? (d) When does f (t) attain its least value? (e) What is the rate of change of f (t) at t = 7.5? (f ) W
> Refer to Fig. 21. Figure 21: (a) Looking at the graph of f ‘(x), determine whether f (x) is increasing or decreasing at x = 9. Look at the graph of f (x) to confirm your answer. (b) Looking at the values of f ‘(x) f
> Differentiate. y = 2 / 1 - 5x
> Suppose that Fig. 20 contains the graph of y = s (t), the distance traveled by a car after t hours. Is the car going faster at t = 1 or t = 2? Figure 20: Figure 20 y 1 2
> The first and second derivatives of the function f (x) have the values given in Table 1. (a) Find the x-coordinates of all relative extreme points. (b) Find the x-coordinates of all inflection points. Table 1: Table 1 Values of the First Two Deriva
> Refer to the graph in Fig. 19. Fill in each box of the grid with either POS, NEG, or 0. Figure 19: Y Figure 19 y = f(x) B x A B C f'
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = 3, f ‘(3) = 1, inflection point at x = 3, f ’’(x) < 0 for x > 3
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = -2, f ‘(3) = 2, f ’’(3) = 3
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = 4, f (3) = - 3/2 , f (3) = -2
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = 1, f ‘(3) = 0, inflection point at x = 3, f ‘(x) > 0 for x > 3
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = -2, f ‘(3) = 0, f ’’(3) = 1
> Use the given information to make a good sketch of the function f (x) near x = 3. f (3) = 4, f ‘(3) = - 1/2, f ’’(3) = 5
> Sketch the graph of a function that has the properties described. f (x) defined only for x ≥ 0; (0, 0) and (5, 6) are on the graph; f ‘(x) > 0 for x ≥ 0; f ’’(x) < 0 for x < 5, f ’’(5) = 0, f ’’(x) > 0 for x > 5.
> Differentiate. y = 1 / 2x + 5
> Differentiate. y = 3√3 x
> Sketch the graph of a function that has the properties described. (0, 6), (2, 3), and (4, 0) are on the graph; f ‘(0) = 0 and f ‘(4) = 0; f ’’(x) < 0 for x < 2, f ’’(2) = 0, f ’’(x) > 0 for x > 2.
> Sketch the graph of a function that has the properties described. (-2, -1) and (2, 5) are on the graph; f ‘(-2) = 0 and f ‘(2) = 0; f ’’(x) > 0 for x < 0, f ’’(0) = 0, f ’’(x) < 0 for x > 0.
> Sketch the graph of a function that has the properties described. f (3) = 5; f (x) > 0 for x < 3, f ‘(3) = 0 and f (x) > 0 for x > 3.
> Sketch the graph of a function that has the properties described. f (-1) = 0; f ‘(x) 6 0 for x < -1, f ‘(-1) = 0 and f ‘(x) > 0 for x > -1.
> Sketch the graph of a function that has the properties described. f (2) = 1; f ‘(2) = 0; concave up for all x.
> Which one of the graphs in Fig. 18 could represent a function f (x) for which f (a) = 0, f ‘(a) 0? Figure 18: y Y Figure 18 a (a) a (c) y Y a (b) a (d) 8
> Which one of the graphs in Fig. 18 could represent a function f (x) for which f (a) > 0, f ‘(a) = 0, and f ’’(a) Figure 18: y Y Figure 18 a (a) a (c) y Y a (b) a (d) 8
> Describe the following graph. THE + Y
> Describe the following graph. 引
> Refer to graphs (a)–(f) in Fig. 19. Figure 19: Which functions have the property that the slope always decreases as x increases? K (a) (c) (e) n Figure 19 (b) 44 Y ㅅ (d) 1 (f) x 2
> Differentiate. y = √(1 + x + x2)
> Refer to graphs (a)–(f) in Fig. 19. Figure 19: Which functions have the property that the slope always increases as x increases? K (a) (c) (e) n Figure 19 (b) 44 Y ㅅ (d) 1 (f) x 2
> Refer to graphs (a)–(f) in Fig. 19. Figure 19: Which functions are decreasing for all x? K (a) (c) (e) n Figure 19 (b) 44 Y ㅅ (d) 1 (f) x 2
> Refer to graphs (a)–(f) in Fig. 19. Figure 19: Which functions are increasing for all x? K (a) (c) (e) n Figure 19 (b) 44 Y ㅅ (d) 1 (f) x 2
> Simultaneously graph the functions y = 1/x + x and y = x in the window [-6, 6] by [-6, 6]. Describe the asymptote of the first function.
> The graph of the function f (x) = 2x2 – 1 / .5x2 + 6 has a horizontal asymptote of the form y = c. Estimate the value of c by graphing f (x) in the window [0, 50] by [-1, 6].
> Graph the function f (x) = 1 / x3 - 2x2 + x - 2 in the window [0, 4] by [-15, 15]. For what value of x does f (x) have a vertical asymptote?
> If the function f (x) has a relative minimum at x = a and a relative maximum at x = b, must f (a) be less than f (b)?
> Consider a smooth curve with no undefined points. (a) If it has two relative maximum points, must it have a relative minimum point? (b) If it has two relative extreme points, must it have an inflection point?
> Sketch the graph of a function having the given properties. Defined for x ≥ 0; absolute minimum value at x = 0; relative maximum point at x = 4; asymptotic to the line y = (x/2) + 1
> Sketch the graph of a function having the given properties. Defined and increasing for all x Ú 0; inflection point at x = 5; asymptotic to the line y = (3/4)x + 5.
> Differentiate. y = √(1 + x2)
> Sketch the graph of a function having the given properties. Relative maximum points at x = 1 and x = 5; relative minimum point at x = 3; inflection points at x = 2 and x = 4
> Sketch the graph of a function having the given properties. Defined for 0 ≤ x ≤ 10; relative maximum point at x = 3; absolute maximum value at x = 10
> Let P(t) be the population of a bacteria culture after t days and suppose that P(t) has the line y = 25,000,000 as an asymptote. What does this imply about the size of the population?
> Let s (t) be the distance (in feet) traveled by a parachutist after t seconds from the time of opening the chute, and suppose that s (t) has the line y = -15t + 10 as an asymptote. What does this imply about the velocity of the parachutist?
> Figure 23 shows the graph of the consumer price index for the years 1983 (t = 0) through 2002 (t = 19). This index measures how much a basket of commodities that costs $100 in the beginning of 1983 would cost at any given time. In what year was the rate
> Figure 22 gives the number of U.S. farms in millions from 1920 (t = 20) to 2000 (t = 100). In what year was the number of farms decreasing most rapidly? Figure 22: U.S. Farms (millions) 52428766 Y HT 0 10 20 30 40 50 60 70 80 90 100 (1900) (2000) T
> Suppose that some organic waste products are dumped into a lake at time t = 0 and that the oxygen content of the lake at time t is given by the graph in Fig. 21. Describe the graph in physical terms. Indicate the significance of the inflection point at t
> One method of determining the level of blood flow through the brain requires the person to inhale air containing a fixed concentration of N2O, nitrous oxide. During the first minute, the concentration of N2O in the jugular vein grows at an increasing rat
> Let C(x) denote the total cost of manufacturing x units of some product. Then C(x) is an increasing function for all x. For small values of x, the rate of increase of C(x) decreases (because of the savings that are possible with “mass production”). Event
> In certain professions, the average annual income has been rising at an increasing rate. Let f (T) denote the average annual income at year T for persons in one of these professions and sketch a graph that could represent f (T).
> Differentiate. y = 3x + π3
> In certain professions, the average annual income has been rising at an increasing rate. Let f (T) denote the average annual income at year T for persons in one of these professions and sketch a graph that could represent f (T).
> The annual world consumption of oil rises each year. Furthermore, the amount of the annual increase in oil consumption is also rising each year. Sketch a graph that could represent the annual world consumption of oil.
> Draw the graph of a function y = f (x) with the stated properties. Both the function and the slope decrease as x increases.
> Draw the graph of a function y = f (x) with the stated properties. The function decreases and the slope increases as x increases.
> Draw the graph of a function y = f (x) with the stated properties. The function increases and the slope decreases as x increases.

