Question: Determine whether the series is conditionally
Determine whether the series is conditionally convergent, absolutely convergent, or divergent.
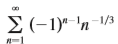
Transcribed Image Text:
E (-1) 'n-1/3
> Determine whether the series converges or diverges. 1 + cos n e"
> Determine whether the series converges or diverges. (2k – 1)(k² – 1) Σ (k + 1)(k² + 4)²
> Determine whether the series converges or diverges. Σ k3 + 4k + 3 k-1
> Determine whether the series converges or diverges. k sin?k 1 1 + k³ WI
> Determine whether the series converges or diverges. In k k k-1
> Determine whether the series converges or diverges. 6" -i 5" - 1
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. et dx 4 - e2*
> Show that if p is an nth-degree polynomial, then p(x + 1) = ' Σ p®(x) i!
> Determine whether the series converges or diverges. 9" Σ 3 + 10"
> Determine whether the series converges or diverges. n - 1 AI n' + 1
> Determine whether the series converges or diverges. n + 1 n/n
> Determine whether the series converges or diverges. Σ In - 1 -2
> Determine whether the series converges or diverges. 1 Σ n' + 8 n-1
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x = y? – 2y, 0 < y< 2
> We arrived at Formula 6.3.2, / by using cylindrical shells, but now we can use integration by parts to prove it using the slicing method of Section 6.2, at least for the case where f is one­ to­ one and therefore has an inverse fu
> For what values of p is each series convergent? (In n)" 2 (-1)* 1 n-2
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. (-9)" Σ n10*+1 n-1
> Find the Taylor polynomial T3(x) for the function f centered at the number a. Graph f and T3 on the same screen. f(x) — х сos x,
> For what values of p is each series convergent? (-1)" -1 n + p
> For what values of p is each series convergent? (-1)* -1 Σ n" n-1
> Approximate the sum of the series correct to four decimal places. (-1)"-1 Σ n 4"
> Approximate the sum of the series correct to four decimal places. E (-1)"ne 2n
> Determine whether the differential equation is linear. — х y tan x
> Approximate the sum of the series correct to four decimal places. i(-1)** -1 ク
> Approximate the sum of the series correct to four decimal places. (-1)" Σ (2n)!
> (a) Use integration by parts to show that (b) If f and t are inverse functions and f9 is continuous, prove that (c) In the case where f and t are positive functions and b > a > 0, draw a diagram to give a geometric interpretation of part (b). (d) U
> Show that the series is convergent. How many terms of the series do we need to add in order to find the sum to the indicated accuracy? (lerror|< 0.00005) n-
> Show that the series is convergent. How many terms of the series do we need to add in order to find the sum to the indicated accuracy? (-1)* Σ n2 2" -' (lerror |< 0.0005) -1
> Show that the series is convergent. How many terms of the series do we need to add in order to find the sum to the indicated accuracy? Σ (-)" (|error|< 0.0005) -1 n
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. 2 + 3n
> Show that the series is convergent. How many terms of the series do we need to add in order to find the sum to the indicated accuracy? (-1)*+1 Σ n° (|error|< 0.00005) n-1
> Graph both the sequence of terms and the sequence of partial sums on the same screen. Use the graph to make a rough estimate of the sum of the series. Then use the Alternating Series Estimation Theorem to estimate the sum correct to four decimal places.
> Graph both the sequence of terms and the sequence of partial sums on the same screen. Use the graph to make a rough estimate of the sum of the series. Then use the Alternating Series Estimation Theorem to estimate the sum correct to four decimal places.
> Determine whether the differential equation is linear. y' + x/y = x?
> Test the series for convergence or divergence. E (-1)"(/n + 1 – Vñ)
> Test the series for convergence or divergence. E(-1)". E(-1)* "". n!
> Test the series for convergence or divergence. E (-1)" cos n-1
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the function and its antiderivative (take C − 0). |x² sin 2x dx
> Show that cosh x ≥1+ 1 2 x2 for all x.
> Evaluate the integral. w/4 (" tan'0 sec?0 do Jo
> Find the area enclosed by the curve in Exercise 29. Data from Exercise 29: At what points does the curve have vertical or horizontal tangents? Use this information to help sketch the curve. X= 2a cos t - a cos 21 y = 2a sin t – a sin 2t
> Find the sum of the series. E [tan '(n + 1) – tan 'n] -1
> Find the sum of the series. 1 Σ п(п + 3)
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the function and its antiderivative (take C = 0). x3/2 In x dx
> Find the sum of the series. (-3)' Σ "-1 3n n-1
> Determine whether the series is conditionally convergent, absolutely convergent, or divergent. (-1)"/n Σ In n n-2
> Determine whether the series is conditionally convergent, absolutely convergent, or divergent. (-1)"(n Σ 22a+1 (-17(л + 1)3" 2n1
> Evaluate the integral. *w/2 · dx m/2 1 + cos'x
> Find the slope of the tangent line to the given curve at the point corresponding to the specified value of the parameter. r3 3 + сos 30; ө — п/2
> Determine whether the series is convergent or divergent. Vn + 1 – Vn – 1 п — R-1
> Determine whether the series is convergent or divergent. E (-1)"-1. n + 1 n-1
> Determine whether the series is convergent or divergent. (-5)2n Σ n²9"
> Determine whether the series is convergent or divergent. 1.3. 5. (2n – 1) R-1 5"n!
> Determine whether the series is absolutely convergent or conditionally convergent. (-1)" Σ n-1 n' + 1 3
> Determine whether the series is convergent or divergent. 2n n° Σ | (1 + 2n²)"
> Determine whether the series is convergent or divergent. cos 3n Σ 1 + (1.2)" n-
> Determine whether the series is convergent or divergent. n Σ E In Зп + 1 n-1
> Evaluate the integral. 1 + 12t dt 1+ 3t
> Determine whether the sequence converges or diverges. If it converges, find the limit. (-1)" - an 2n
> Determine whether the series is convergent or divergent. 1 Σ n=2 n/In n
> Determine whether the series is convergent or divergent. (-1)" Σ Vn + 1
> Determine whether the series is convergent or divergent. n? + 1 Σ n3 + 1
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the function and its antiderivative (take C − 0). 2% dx Sxe
> A sequence is defined recursively by the equations a1 = 1, an+1 = 1 3 (a n +4). Show that {an} is increasing and an < 2 for all n. Deduce that / is convergent and find its limit.
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. {(-10)"/n!}
> Evaluate the integral. | tan?x dx
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. {(1 + 3/n)+"}
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. In n an in
> Find the Taylor polynomial T3(x) for the function f centered at the number a. Graph f and T3 on the same screen. f(x) cos х, a = T /2
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. а, — сos(пт/2)
> Sketch the parametric curve and eliminate the parameter to find the Cartesian equation of the curve. х — cos 0, у —sec 0, 0 <0 < п/2
> Sketch the parametric curve and eliminate the parameter to find the Cartesian equation of the curve. х —1+ е", у — е' y
> First make a substitution and then use integration by parts to evaluate the integral. arcsin(In x) dx
> Sketch the parametric curve and eliminate the parameter to find the Cartesian equation of the curve. x = t² + 4t, y = 2 – 1, -4 < t<1
> Evaluate the integral. ax
> The astronomer Giovanni Cassini (1625–1712) studied the family of curves with polar equations where a and c are positive real numbers. These curves are called the ovals of Cassini even though they are oval shaped only for certain values
> A family of curves has polar equations Investigate how the graph changes as the number a changes. In particular, you should identify the transitional values of a for which the basic shape of the curve changes. 1 — а сos0 1+а сos0
> Use your graph in Problem 3 to estimate the value of / for which f(/) is a maximum under Planck’s Law. Data from Problem 3: Graph f as given by both laws on the same screen and comment on the similarities and differences. Use T = 5700 K (the temperatur
> Use the Maclaurin series for cos x to compute cos 58 correct to five decimal places.
> Graph f as given by both laws on the same screen and comment on the similarities and differences. Use T = 5700 K (the temperature of the sun). (You may want to change from meters to the more convenient unit of micrometers: 1 mm − 1026 m.)
> Use a Taylor polynomial to show that, for large wavelengths, Planck’s Law gives approximately the same values as the Rayleigh-Jeans Law.
> Use l’ Hospital’s Rule to show that for Planck’s Law. So this law models blackbody radiation better than the Rayleigh-Jeans Law for short wavelengths. lim f(A) = 0 and lim f(A) = 0 %3D %3D A0+
> First make a substitution and then use integration by parts to evaluate the integral. e In(1 + x) dx
> Evaluate the integral.
> Evaluate the integral. t² sin ßt dt 2
> Investigate how the graph off changes as T varies. (Use Planck’s Law.) In particular, graph f for the stars Betelgeuse (T = 3400 K), Procyon (T = 6400 K), and Sirius (T = 9200 K), as well as the sun. How does the total radiation emitted (the area under t
> Use a computer algebra system to find the exact area of the surface obtained by rotating the curve / Then approximate your result to three decimal places.
> Find the volume of the solid obtained by rotating the region of Problem 2 about the line y = x - 2. Data from Problem 2: Find the area of the region shown in the figure below. yA (2π, 2π) y=x+ sin x y=x- 2
> Find a formula (similar to the one in Problem 1) for the volume of the solid obtained by rotating 5 about the line y = mx + b. Data from Problem 1: Show that the area of / is R
> Find the area of the region shown in the figure below. yA (2π, 2π) y=x+ sin x y=x- 2
> Show that the area of R is 1 I[S«) – mx — b][1 + mf()] dx 1 + m?
> Find the Maclaurin series of f (by any method) and its radius of convergence. Graph f and its first few Taylor polynomials on the same screen. What do you notice about the relationship between these polynomials and f? f(x) = tan '(x³) S(x).
> If the circle C rolls on the outside of the fixed circle, the curve traced out by P is called an epicycloid. Find parametric equations for the epicycloid.
> Evaluate the integral. evi
> First make a substitution and then use integration by parts to evaluate the integral. ec sin 21 dt cos! Jo
> Now try b = 1 and a = n/d, a fraction where n and d have no common factor. First let n = 1 and try to determine graphically the effect of the denominator d on the shape of the graph. Then let n vary while keeping d constant. What happens when n = d + 1?
> Use a graphing device (or the interactive graphic in TEC Module 10.1B) to draw the graphs of hypocycloids with a positive integer and b = 1. How does the value of a affect the graph? Show that if we take a = 4, then the parametric equations of the hypocy
> (a) Every elementary function has an elementary derivative. (b) Every elementary function has an elementary antiderivative.
> Determine whether the sequence converges or diverges. If it converges, find the limit. n! 2"
> Find the Maclaurin series of f (by any method) and its radius of convergence. Graph f and its first few Taylor polynomials on the same screen. What do you notice about the relationship between these polynomials and f? f(a) — хе

