Question: Determine whether the two random variables of
Determine whether the two random variables of Exercise 3.44 are dependent or independent.
Exercise 3.44:
Each rear tire on an experimental airplane is supposed to be filled to a pressure of 40 pounds per square inch (psi). Let X denote the actual air pressure for the right tire and Y denote the actual air pressure for the left tire. Suppose that X and Y are random variables with the joint density function
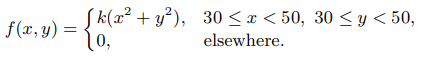
Transcribed Image Text:
( k(x² + y²), 30
> Suppose that the four inspectors at a film factory are supposed to stamp the expiration date on each package of film at the end of the assembly line. John, who stamps 20% of the packages, fails to stamp the expiration date once in every 200 packages; Tom
> If the person in Exercise 2.96 received a speeding ticket on her way to work, what is the probability that she passed through the radar trap located at L2? Exercise 2.96: Police plan to enforce speed limits by using radar traps at four different locatio
> Referring to Exercise 2.95, what is the probability that a person diagnosed as having cancer actually has the disease? Exercise 2.95: In a certain region of the country it is known from past experience that the probability of selecting an adult over 40
> Police plan to enforce speed limits by using radar traps at four different locations within the city limits. The radar traps at each of the locations L1, L2, L3, and L4 will be operated 40%, 30%, 20%, and 30% of the time. If a person who is speeding on h
> In a certain region of the country it is known from past experience that the probability of selecting an adult over 40 years of age with cancer is 0.05. If the probability of a doctor correctly diagnosing a person with cancer as having the disease is 0.7
> In the situation of Exercise 2.93, it is known that the system does not work. What is the probability that the component A also does not work?
> A circuit system is given in Figure 2.11. Assume the components fail independently. (a) What is the probability that the entire system works? (b) Given that the system works, what is the probability that the component A is not working? Figure 2.11:
> Suppose the diagram of an electrical system is as given in Figure 2.10. What is the probability that the system works? Assume the components fail independently. Figure 2.10: 0.7 B 0.95 0.9 A D 0.8 Figure 2.10: Diagram for Exercise 2.92.
> Find the probability of randomly selecting 4 good quarts of milk in succession from a cooler containing 20 quarts of which 5 have spoiled, by using (a) the first formula of Theorem 2.12 on page 68; (b) the formulas of Theorem 2.6 and Rule 2.3 on pages 50
> If 7 cards are dealt from an ordinary deck of 52 playing cards, what is the probability that (a) exactly 2 of them will be face cards? (b) at least 1 of them will be a queen?
> Pollution of the rivers in the United States has been a problem for many years. Consider the following events: A: the river is polluted, B: a sample of water tested detects pollution, C: fishing is permitted. Assume P(A) = 0.3, P(B|A) = 0.75, P(B|A’) = 0
> The proportion of people who respond to a certain mail-order solicitation is a continuous random variable X that has the density function (a) Show that P(0 (b) Find the probability that more than 1/4 but fewer than 1/2 of the people contacted will resp
> A town has two fire engines operating independently. The probability that a specific engine is available when needed is 0.96. (a) What is the probability that neither is available when needed? (b) What is the probability that a fire engine is available w
> Before the distribution of certain statistical software, every fourth compact disk (CD) is tested for accuracy. The testing process consists of running four independent programs and checking the results. The failure rates for the four testing programs ar
> A real estate agent has 8 master keys to open several new homes. Only 1 master key will open any given house. If 40% of these homes are usually left unlocked, what is the probability that the real estate agent can get into a specific home if the agent se
> In 1970, 11% of Americans completed four years of college; 43% of them were women. In 1990, 22% of Americans completed four years of college; 53% of them were women (Time, Jan. 19, 1996). (a) Given that a person completed four years of college in 1970, w
> The probability that a doctor correctly diagnoses a particular illness is 0.7. Given that the doctor makes an incorrect diagnosis, the probability that the patient files a lawsuit is 0.9. What is the probability that the doctor makes an incorrect diagnos
> The probability that the head of a household is home when a telemarketing representative calls is 0.4. Given that the head of the house is home, the probability that goods will be bought from the company is 0.3. Find the probability that the head of the
> The probability that a vehicle entering the Luray Caverns has Canadian license plates is 0.12; the probability that it is a camper is 0.28; and the probability that it is a camper with Canadian license plates is 0.09. What is the probability that (a) a c
> For married couples living in a certain suburb, the probability that the husband will vote on a bond referendum is 0.21, the probability that the wife will vote on the referendum is 0.28, and the probability that both the husband and the wife will vote i
> From a lot of 10 missiles, 4 are selected at random and fired. If the lot contains 3 defective missiles that will not fire, what is the probability that (a) all 4 will fire? (b) at most 2 will not fire?
> The probability that a married man watches a certain television show is 0.4, and the probability that a married woman watches the show is 0.5. The probability that a man watches the show, given that his wife does, is 0.7. Find the probability that (a) a
> Consider a system of components in which there are 5 independent components, each of which possesses an operational probability of 0.92. The system does have a redundancy built in such that it does not fail if 3 out of the 5 components are operational. W
> Find the probability distribution of the random variable W in Exercise 3.3, assuming that the coin is biased so that a head is twice as likely to occur as a tail. Exercise 3.3: Let W be a random variable giving the number of heads minus the number of ta
> Another type of system that is employed in engineering work is a group of parallel components or a parallel system. In this more conservative approach, the probability that the system operates is larger than the probability that any component operates. T
> The behavior of series of components plays a huge role in scientific and engineering reliability problems. The reliability of the entire system is certainly no better than that of the weakest component in the series. In a series system, the components op
> Consider the random variables X and Y that represent the number of vehicles that arrive at two separate street corners during a certain 2-minute period. These street corners are fairly close together so it is important that traffic engineers deal with th
> Consider the situation of Review Exercise 3.75. But suppose the joint distribution of the two proportions is given by (a) Give the marginal distribution fX1 (x1) of the proportion X1 and verify that it is a valid density function. (b) What is the proba
> A chemical system that results from a chemical reaction has two important components among others in a blend. The joint distribution describing the proportions X1 and X2 of these two components is given by (a) Give the marginal distribution of X1. (b)
> The time Z in minutes between calls to an electrical supply system has the probability density function (a) What is the probability that there are no calls within a 20-minute time interval? (b) What is the probability that the first call comes within 1
> Impurities in a batch of final product of a chemical process often reflect a serious problem. From considerable plant data gathered, it is known that the proportion Y of impurities in a batch has a density function given by (a) Verify that the above is
> A random committee of size 3 is selected from 4 doctors and 2 nurses. Write a formula for the probability distribution of the random variable X representing the number of doctors on the committee. Find P(2 ≤ X ≤ 3).
> Passenger congestion is a service problem in airports. Trains are installed within the airport to reduce the congestion. With the use of the train, the time X in minutes that it takes to travel from the main terminal to a particular concourse has density
> The shelf life of a product is a random variable that is related to consumer acceptance. It turns out that the shelf life Y in days of a certain type of bakery product has a density function What fraction of the loaves of this product stocked today wou
> Pairs of pants are being produced by a particular outlet facility. The pants are checked by a group of 10 workers. The workers inspect pairs of pants taken randomly from the production line. Each inspector is assigned a number from 1 through 10. A buyer
> The total number of hours, measured in units of 100 hours, that a family runs a vacuum cleaner over a period of one year is a continuous random variable X that has the density function Find the probability that over a period of one year, a family runs
> The life span in hours of an electrical component is a random variable with cumulative distribution function (a) Determine its probability density function. (b) Determine the probability that the life span of such a component will exceed 70 hours.
> Consider the following joint probability density function of the random variables X and Y: (a) Find the marginal density functions of X and Y. (b) Are X and Y independent? (c) Find P(X > 2). 3*-, 1<x < 3, 1< y < 2, 0, f(x, y) = elsewhere.
> An industrial process manufactures items that can be classified as either defective or not defective. The probability that an item is defective is 0.1. An experiment is conducted in which 5 items are drawn randomly from the process. Let the random variab
> Consider the random variables X and Y with joint density function (a) Find the marginal distributions of X and Y . (b) Find P(X > 0.5,Y > 0.5). Sr +y, 0<x, y <1, 10, f(x, y) = elsewhere.
> Let the number of phone calls received by a switchboard during a 5-minute interval be a random variable X with probability function (a) Determine the probability that X equals 0, 1, 2, 3, 4, 5, and 6. (b) Graph the probability mass function for these v
> A service facility operates with two service lines. On a randomly selected day, let X be the proportion of time that the first line is in use whereas Y is the proportion of time that the second line is in use. Suppose that the joint probability density f
> To avoid detection at customs, a traveler places 6 narcotic tablets in a bottle containing 9 vitamin tablets that are similar in appearance. If the customs official selects 3 of the tablets at random for analysis, what is the probability that the travele
> An employee is selected from a staff of 10 to supervise a certain project by selecting a tag at random from a box containing 10 tags numbered from 1 to 10. Find the formula for the probability distribution of X representing the number on the tag that is
> Two electronic components of a missile system work in harmony for the success of the total system. Let X and Y denote the life in hours of the two components. The joint density of X and Y is (a) Give the marginal density functions for both random varia
> An insurance company offers its policyholders a number of different premium payment options. For a randomly selected policyholder, let X be the number of months between successive payments. The cumulative distribution function of X is (a) What is the p
> A tobacco company produces blends of tobacco, with each blend containing various proportions of Turkish, domestic, and other tobaccos. The proportions of Turkish and domestic in a blend are random variables with joint density function (X = Turkish and Y
> The joint probability density function of the random variables X, Y, and Z is Find (a) the joint marginal density function of Y and Z; (b) the marginal density of Y; (c) P( 1 4 1 3 , 1 (d) P(0 4xyz? , 0< x, Y < 1, 0 < z < 3, f(x, y, z) = 0, elsewh
> The shelf life, in days, for bottles of a certain prescribed medicine is a random variable having the density function Find the probability that a bottle of this medicine will have a shell life of (a) at least 200 days; (b) anywhere from 80 to 120 days
> Determine whether the two random variables of Exercise 3.43 are dependent or independent. Exercise 3.43: Let X denote the reaction time, in seconds, to a certain stimulus and Y denote the temperature (â—¦F) at which a certain reaction
> Let X, Y, and Z have the joint probability density function (a) Find k. (b) Find P(X 1 2 , 1 S kxy°z, 0< x, y < 1, 0 < z < 2, 10, f(x, y, z) = elsewhere.
> The joint density function of the random variables X and Y is (a) Show that X and Y are not independent. (b) Find P(X > 0.3 | Y = 0.5). f (x, y) S6x, 0< x < 1, 0 < y <1 – x, 1o, elsewhere.
> Determine whether the two random variables of Exercise 3.50 are dependent or independent. Exercise 3.50: Suppose that X and Y have the following joint probability distribution: f(x, y) 2 4 1 0.10 0.15 0.20 0.30 0.10 0.15
> A homeowner plants 6 bulbs selected at random from a box containing 5 tulip bulbs and 4 daffodil bulbs. What is the probability that he planted 2 daffodil bulbs and 4 tulip bulbs?
> Determine whether the two random variables of Exercise 3.49 are dependent or independent. Exercise 3.49: Let X denote the number of times a certain numerical control machine will malfunction: 1, 2, or 3 times on any given day. Let Y denote the number of
> Given the joint density function find P(1 ーエー2,0<z< 2, 2<y<4, f(x, y) = elsewhere,
> A coin is tossed twice. Let Z denote the number of heads on the first toss and W the total number of heads on the 2 tosses. If the coin is unbalanced and a head has a 40% chance of occurring, find (a) the joint probability distribution of W and Z; (b) th
> Three cards are drawn without replacement from the 12 face cards (jacks, queens, and kings) of an ordinary deck of 52 playing cards. Let X be the number of kings selected and Y the number of jacks. Find (a) the joint probability distribution of X and Y;
> Suppose that X and Y have the following joint probability distribution: (a) Find the marginal distribution of X. (b) Find the marginal distribution of Y. f(x, y) 2 4 1 0.10 0.15 0.20 0.30 0.10 0.15
> Let X denote the number of times a certain numerical control machine will malfunction: 1, 2, or 3 times on any given day. Let Y denote the number of times a technician is called on an emergency call. Their joint probability distribution is given as (a)
> Referring to Exercise 3.39, find (a) f(y|2) for all values of y; (b) P(Y = 0 | X = 2). Exercise 3.39: From a sack of fruit containing 3 oranges, 2 apples, and 3 bananas, a random sample of 4 pieces of fruit is selected. If X is the number of oranges and
> The amount of kerosene, in thousands of liters, in a tank at the beginning of any day is a random amount Y from which a random amount X is sold during that day. Suppose that the tank is not resupplied during the day so that x ≤ y, and
> A manufacturer knows that on average 20% of the electric toasters produced require repairs within 1 year after they are sold. When 20 toasters are randomly selected, find appropriate numbers x and y such that (a) the probability that at least x of them w
> Let X denote the diameter of an armored electric cable and Y denote the diameter of the ceramic mold that makes the cable. Both X and Y are scaled so that they range between 0 and 1. Suppose that X and Y have the joint density Find P(X + Y > 1/2).
> Each rear tire on an experimental airplane is supposed to be filled to a pressure of 40 pounds per square inch (psi). Let X denote the actual air pressure for the right tire and Y denote the actual air pressure for the left tire. Suppose that X and Y are
> Let X denote the reaction time, in seconds, to a certain stimulus and Y denote the temperature (â—¦F) at which a certain reaction starts to take place. Suppose that two random variables X and Y have the joint density Find (a) P(0 &aci
> Let X and Y denote the lengths of life, in years, of two components in an electronic system. If the joint density function of these variables is find P(0 Se-(z+y), x> 0, y > 0, 10, т > 0, у > 0, elsewhere, f(x, y) :
> A candy company distributes boxes of chocolates with a mixture of creams, toffees, and cordials. Suppose that the weight of each box is 1 kilogram, but the individual weights of the creams, toffees, and cordials vary from box to box. For a randomly selec
> A fast-food restaurant operates both a drive through facility and a walk-in facility. On a randomly selected day, let X and Y, respectively, be the proportions of the time that the drive-through and walk-in facilities are in use, and suppose that the joi
> A coin is flipped until 3 heads in succession occur. List only those elements of the sample space that require 6 or less tosses. Is this a discrete sample space? Explain.
> From a sack of fruit containing 3 oranges, 2 apples, and 3 bananas, a random sample of 4 pieces of fruit is selected. If X is the number of oranges and Y is the number of apples in the sample, find (a) the joint probability distribution of X and Y; (b)
> Determine the values of c so that the following functions represent joint probability distributions of the random variables X and Y: (a) f(x, y) = cxy, for x = 1, 2, 3; y = 1, 2, 3; (b) f(x, y) = c|x − y|, for x = −2, 0, 2; y = −2, 3.
> If the probability that a fluorescent light has a useful life of at least 800 hours is 0.9, find the probabilities that among 20 such lights (a) exactly 18 will have a useful life of at least 800 hours; (b) at least 15 will have a useful life of at least
> On a laboratory assignment, if the equipment is working, the density function of the observed outcome, X, is (a) Calculate P(X ≤ 1/3). (b) What is the probability that X will exceed 0.5? (c) Given that X ≥ 0.5, what
> Suppose it is known from large amounts of historical data that X, the number of cars that arrive at a specific intersection during a 20-second time period, is characterized by the following discrete probability function: (a) Find the probability that i
> Magnetron tubes are produced on an automated assembly line. A sampling plan is used periodically to assess quality of the lengths of the tubes. This measurement is subject to uncertainty. It is thought that the probability that a random tube meets length
> Suppose a certain type of small data processing firm is so specialized that some have difficulty making a profit in their first year of operation. The probability density function that characterizes the proportion Y that make a profit is given by (a) W
> The proportion of the budget for a certain type of industrial company that is allotted to environmental and pollution control is coming under scrutiny. A data collection project determines that the distribution of these proportions is given by (a) Veri
> Based on extensive testing, it is determined by the manufacturer of a washing machine that the time Y (in years) before a major repair is required is characterized by the probability density function (a) Critics would certainly consider the product a b
> Measurements of scientific systems are always subject to variation, some more than others. There are many structures for measurement error, and statisticians spend a great deal of time modeling these errors. Suppose the measurement error X of a certain p
> Let W be a random variable giving the number of heads minus the number of tails in three tosses of a coin. List the elements of the sample space S for the three tosses of the coin and to each sample point assign a value w of W.
> An important factor in solid missile fuel is the particle size distribution. Significant problems occur if the particle sizes are too large. From production data in the past, it has been determined that the particle size (in micrometers) distribution is
> A cereal manufacturer is aware that the weight of the product in the box varies slightly from box to box. In fact, considerable historical data have allowed the determination of the density function that describes the probability structure for the weight
> Assuming that 6 in 10 automobile accidents are due mainly to a speed violation, find the probability that among 8 automobile accidents, 6 will be due mainly to a speed violation (a) by using the formula for the binomial distribution; (b) by using Table A
> The time to failure in hours of an important piece of electronic equipment used in a manufactured DVD player has the density function (a) Find F(x). (b) Determine the probability that the component (and thus the DVD player) lasts more than 1000 hours b
> From a box containing 4 black balls and 2 green balls, 3 balls are drawn in succession, each ball being replaced in the box before the next draw is made. Find the probability distribution for the number of green balls.
> From a box containing 4 dimes and 2 nickels, 3 coins are selected at random without replacement. Find the probability distribution for the total T of the 3 coins. Express the probability distribution graphically as a probability histogram.
> Find the probability distribution for the number of jazz CDs when 4 CDs are selected at random from a collection consisting of 5 jazz CDs, 2 classical CDs, and 3 rock CDs. Express your results by means of a formula.
> Find the cumulative distribution function of the random variable W in Exercise 3.8. Using F(w), find (a) P(W >0); (b) P(−1 ≤W
> Three cards are drawn in succession from a deck without replacement. Find the probability distribution for the number of spades.
> Consider the density function (a) Evaluate k. (b) Find F(x) and use it to evaluate P(0.3
> For the density function of Exercise 3.18, find F(x), and use it to evaluate P(3 ≤X
> An overseas shipment of 5 foreign automobiles contains 2 that have slight paint blemishes. If an agency receives 3 of these automobiles at random, list the elements of the sample space S, using the letters B and N for blemished and non-blemished, respect
> For the density function of Exercise 3.17, find F(x). Use it to evaluate P(2 < X < 2.5). Exercise 3.17: A continuous random variable X that can assume values between x = 1 and x = 3 has a density function given by f(x) = 1/2.
> Suppose that for a very large shipment of integrated-circuit chips, the probability of failure for any one chip is 0.10. Assuming that the assumptions underlying the binomial distributions are met, find the probability that at most 3 chips fail in a rand
> A continuous random variable X that can assume values between x = 2 and x = 5 has a density function given by f(x) = 2(1 + x)/27. Find (a) P(X
> A continuous random variable X that can assume values between x = 1 and x = 3 has a density function given by f(x) = 1/2. (a) Show that the area under the curve is equal to 1. (b) Find P(2 < X < 2.5). (c) Find P(X ≤ 1.6).
> Construct a graph of the cumulative distribution function of Exercise 3.15.
> Find the cumulative distribution function of the random variable X representing the number of defectives in Exercise 3.11. Then using F(x), find (a) P(X = 1); (b) P(0 < X ≤ 2).
> The waiting time, in hours, between successive speeders spotted by a radar unit is a continuous random variable with cumulative distribution function Find the probability of waiting less than 12 minutes between successive speeders (a) using the cumulat

