Question: The proportion of the budget for a
The proportion of the budget for a certain type of industrial company that is allotted to environmental and pollution control is coming under scrutiny. A data collection project determines that the distribution of these proportions is given by
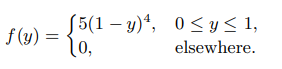
(a) Verify that the above is a valid density function.
(b) What is the probability that a company chosen at random expends less than 10% of its budget on environmental and pollution controls?
(c) What is the probability that a company selected at random spends more than 50% of its budget on environmental and pollution controls?
Transcribed Image Text:
> The time Z in minutes between calls to an electrical supply system has the probability density function (a) What is the probability that there are no calls within a 20-minute time interval? (b) What is the probability that the first call comes within 1
> Impurities in a batch of final product of a chemical process often reflect a serious problem. From considerable plant data gathered, it is known that the proportion Y of impurities in a batch has a density function given by (a) Verify that the above is
> A random committee of size 3 is selected from 4 doctors and 2 nurses. Write a formula for the probability distribution of the random variable X representing the number of doctors on the committee. Find P(2 ≤ X ≤ 3).
> Passenger congestion is a service problem in airports. Trains are installed within the airport to reduce the congestion. With the use of the train, the time X in minutes that it takes to travel from the main terminal to a particular concourse has density
> The shelf life of a product is a random variable that is related to consumer acceptance. It turns out that the shelf life Y in days of a certain type of bakery product has a density function What fraction of the loaves of this product stocked today wou
> Pairs of pants are being produced by a particular outlet facility. The pants are checked by a group of 10 workers. The workers inspect pairs of pants taken randomly from the production line. Each inspector is assigned a number from 1 through 10. A buyer
> The total number of hours, measured in units of 100 hours, that a family runs a vacuum cleaner over a period of one year is a continuous random variable X that has the density function Find the probability that over a period of one year, a family runs
> The life span in hours of an electrical component is a random variable with cumulative distribution function (a) Determine its probability density function. (b) Determine the probability that the life span of such a component will exceed 70 hours.
> Consider the following joint probability density function of the random variables X and Y: (a) Find the marginal density functions of X and Y. (b) Are X and Y independent? (c) Find P(X > 2). 3*-, 1<x < 3, 1< y < 2, 0, f(x, y) = elsewhere.
> An industrial process manufactures items that can be classified as either defective or not defective. The probability that an item is defective is 0.1. An experiment is conducted in which 5 items are drawn randomly from the process. Let the random variab
> Consider the random variables X and Y with joint density function (a) Find the marginal distributions of X and Y . (b) Find P(X > 0.5,Y > 0.5). Sr +y, 0<x, y <1, 10, f(x, y) = elsewhere.
> Let the number of phone calls received by a switchboard during a 5-minute interval be a random variable X with probability function (a) Determine the probability that X equals 0, 1, 2, 3, 4, 5, and 6. (b) Graph the probability mass function for these v
> A service facility operates with two service lines. On a randomly selected day, let X be the proportion of time that the first line is in use whereas Y is the proportion of time that the second line is in use. Suppose that the joint probability density f
> To avoid detection at customs, a traveler places 6 narcotic tablets in a bottle containing 9 vitamin tablets that are similar in appearance. If the customs official selects 3 of the tablets at random for analysis, what is the probability that the travele
> An employee is selected from a staff of 10 to supervise a certain project by selecting a tag at random from a box containing 10 tags numbered from 1 to 10. Find the formula for the probability distribution of X representing the number on the tag that is
> Two electronic components of a missile system work in harmony for the success of the total system. Let X and Y denote the life in hours of the two components. The joint density of X and Y is (a) Give the marginal density functions for both random varia
> An insurance company offers its policyholders a number of different premium payment options. For a randomly selected policyholder, let X be the number of months between successive payments. The cumulative distribution function of X is (a) What is the p
> A tobacco company produces blends of tobacco, with each blend containing various proportions of Turkish, domestic, and other tobaccos. The proportions of Turkish and domestic in a blend are random variables with joint density function (X = Turkish and Y
> The joint probability density function of the random variables X, Y, and Z is Find (a) the joint marginal density function of Y and Z; (b) the marginal density of Y; (c) P( 1 4 1 3 , 1 (d) P(0 4xyz? , 0< x, Y < 1, 0 < z < 3, f(x, y, z) = 0, elsewh
> The shelf life, in days, for bottles of a certain prescribed medicine is a random variable having the density function Find the probability that a bottle of this medicine will have a shell life of (a) at least 200 days; (b) anywhere from 80 to 120 days
> Determine whether the two random variables of Exercise 3.44 are dependent or independent. Exercise 3.44: Each rear tire on an experimental airplane is supposed to be filled to a pressure of 40 pounds per square inch (psi). Let X denote the actual air pr
> Determine whether the two random variables of Exercise 3.43 are dependent or independent. Exercise 3.43: Let X denote the reaction time, in seconds, to a certain stimulus and Y denote the temperature (â—¦F) at which a certain reaction
> Let X, Y, and Z have the joint probability density function (a) Find k. (b) Find P(X 1 2 , 1 S kxy°z, 0< x, y < 1, 0 < z < 2, 10, f(x, y, z) = elsewhere.
> The joint density function of the random variables X and Y is (a) Show that X and Y are not independent. (b) Find P(X > 0.3 | Y = 0.5). f (x, y) S6x, 0< x < 1, 0 < y <1 – x, 1o, elsewhere.
> Determine whether the two random variables of Exercise 3.50 are dependent or independent. Exercise 3.50: Suppose that X and Y have the following joint probability distribution: f(x, y) 2 4 1 0.10 0.15 0.20 0.30 0.10 0.15
> A homeowner plants 6 bulbs selected at random from a box containing 5 tulip bulbs and 4 daffodil bulbs. What is the probability that he planted 2 daffodil bulbs and 4 tulip bulbs?
> Determine whether the two random variables of Exercise 3.49 are dependent or independent. Exercise 3.49: Let X denote the number of times a certain numerical control machine will malfunction: 1, 2, or 3 times on any given day. Let Y denote the number of
> Given the joint density function find P(1 ーエー2,0<z< 2, 2<y<4, f(x, y) = elsewhere,
> A coin is tossed twice. Let Z denote the number of heads on the first toss and W the total number of heads on the 2 tosses. If the coin is unbalanced and a head has a 40% chance of occurring, find (a) the joint probability distribution of W and Z; (b) th
> Three cards are drawn without replacement from the 12 face cards (jacks, queens, and kings) of an ordinary deck of 52 playing cards. Let X be the number of kings selected and Y the number of jacks. Find (a) the joint probability distribution of X and Y;
> Suppose that X and Y have the following joint probability distribution: (a) Find the marginal distribution of X. (b) Find the marginal distribution of Y. f(x, y) 2 4 1 0.10 0.15 0.20 0.30 0.10 0.15
> Let X denote the number of times a certain numerical control machine will malfunction: 1, 2, or 3 times on any given day. Let Y denote the number of times a technician is called on an emergency call. Their joint probability distribution is given as (a)
> Referring to Exercise 3.39, find (a) f(y|2) for all values of y; (b) P(Y = 0 | X = 2). Exercise 3.39: From a sack of fruit containing 3 oranges, 2 apples, and 3 bananas, a random sample of 4 pieces of fruit is selected. If X is the number of oranges and
> The amount of kerosene, in thousands of liters, in a tank at the beginning of any day is a random amount Y from which a random amount X is sold during that day. Suppose that the tank is not resupplied during the day so that x ≤ y, and
> A manufacturer knows that on average 20% of the electric toasters produced require repairs within 1 year after they are sold. When 20 toasters are randomly selected, find appropriate numbers x and y such that (a) the probability that at least x of them w
> Let X denote the diameter of an armored electric cable and Y denote the diameter of the ceramic mold that makes the cable. Both X and Y are scaled so that they range between 0 and 1. Suppose that X and Y have the joint density Find P(X + Y > 1/2).
> Each rear tire on an experimental airplane is supposed to be filled to a pressure of 40 pounds per square inch (psi). Let X denote the actual air pressure for the right tire and Y denote the actual air pressure for the left tire. Suppose that X and Y are
> Let X denote the reaction time, in seconds, to a certain stimulus and Y denote the temperature (â—¦F) at which a certain reaction starts to take place. Suppose that two random variables X and Y have the joint density Find (a) P(0 &aci
> Let X and Y denote the lengths of life, in years, of two components in an electronic system. If the joint density function of these variables is find P(0 Se-(z+y), x> 0, y > 0, 10, т > 0, у > 0, elsewhere, f(x, y) :
> A candy company distributes boxes of chocolates with a mixture of creams, toffees, and cordials. Suppose that the weight of each box is 1 kilogram, but the individual weights of the creams, toffees, and cordials vary from box to box. For a randomly selec
> A fast-food restaurant operates both a drive through facility and a walk-in facility. On a randomly selected day, let X and Y, respectively, be the proportions of the time that the drive-through and walk-in facilities are in use, and suppose that the joi
> A coin is flipped until 3 heads in succession occur. List only those elements of the sample space that require 6 or less tosses. Is this a discrete sample space? Explain.
> From a sack of fruit containing 3 oranges, 2 apples, and 3 bananas, a random sample of 4 pieces of fruit is selected. If X is the number of oranges and Y is the number of apples in the sample, find (a) the joint probability distribution of X and Y; (b)
> Determine the values of c so that the following functions represent joint probability distributions of the random variables X and Y: (a) f(x, y) = cxy, for x = 1, 2, 3; y = 1, 2, 3; (b) f(x, y) = c|x − y|, for x = −2, 0, 2; y = −2, 3.
> If the probability that a fluorescent light has a useful life of at least 800 hours is 0.9, find the probabilities that among 20 such lights (a) exactly 18 will have a useful life of at least 800 hours; (b) at least 15 will have a useful life of at least
> On a laboratory assignment, if the equipment is working, the density function of the observed outcome, X, is (a) Calculate P(X ≤ 1/3). (b) What is the probability that X will exceed 0.5? (c) Given that X ≥ 0.5, what
> Suppose it is known from large amounts of historical data that X, the number of cars that arrive at a specific intersection during a 20-second time period, is characterized by the following discrete probability function: (a) Find the probability that i
> Magnetron tubes are produced on an automated assembly line. A sampling plan is used periodically to assess quality of the lengths of the tubes. This measurement is subject to uncertainty. It is thought that the probability that a random tube meets length
> Suppose a certain type of small data processing firm is so specialized that some have difficulty making a profit in their first year of operation. The probability density function that characterizes the proportion Y that make a profit is given by (a) W
> Based on extensive testing, it is determined by the manufacturer of a washing machine that the time Y (in years) before a major repair is required is characterized by the probability density function (a) Critics would certainly consider the product a b
> Measurements of scientific systems are always subject to variation, some more than others. There are many structures for measurement error, and statisticians spend a great deal of time modeling these errors. Suppose the measurement error X of a certain p
> Let W be a random variable giving the number of heads minus the number of tails in three tosses of a coin. List the elements of the sample space S for the three tosses of the coin and to each sample point assign a value w of W.
> An important factor in solid missile fuel is the particle size distribution. Significant problems occur if the particle sizes are too large. From production data in the past, it has been determined that the particle size (in micrometers) distribution is
> A cereal manufacturer is aware that the weight of the product in the box varies slightly from box to box. In fact, considerable historical data have allowed the determination of the density function that describes the probability structure for the weight
> Assuming that 6 in 10 automobile accidents are due mainly to a speed violation, find the probability that among 8 automobile accidents, 6 will be due mainly to a speed violation (a) by using the formula for the binomial distribution; (b) by using Table A
> The time to failure in hours of an important piece of electronic equipment used in a manufactured DVD player has the density function (a) Find F(x). (b) Determine the probability that the component (and thus the DVD player) lasts more than 1000 hours b
> From a box containing 4 black balls and 2 green balls, 3 balls are drawn in succession, each ball being replaced in the box before the next draw is made. Find the probability distribution for the number of green balls.
> From a box containing 4 dimes and 2 nickels, 3 coins are selected at random without replacement. Find the probability distribution for the total T of the 3 coins. Express the probability distribution graphically as a probability histogram.
> Find the probability distribution for the number of jazz CDs when 4 CDs are selected at random from a collection consisting of 5 jazz CDs, 2 classical CDs, and 3 rock CDs. Express your results by means of a formula.
> Find the cumulative distribution function of the random variable W in Exercise 3.8. Using F(w), find (a) P(W >0); (b) P(−1 ≤W
> Three cards are drawn in succession from a deck without replacement. Find the probability distribution for the number of spades.
> Consider the density function (a) Evaluate k. (b) Find F(x) and use it to evaluate P(0.3
> For the density function of Exercise 3.18, find F(x), and use it to evaluate P(3 ≤X
> An overseas shipment of 5 foreign automobiles contains 2 that have slight paint blemishes. If an agency receives 3 of these automobiles at random, list the elements of the sample space S, using the letters B and N for blemished and non-blemished, respect
> For the density function of Exercise 3.17, find F(x). Use it to evaluate P(2 < X < 2.5). Exercise 3.17: A continuous random variable X that can assume values between x = 1 and x = 3 has a density function given by f(x) = 1/2.
> Suppose that for a very large shipment of integrated-circuit chips, the probability of failure for any one chip is 0.10. Assuming that the assumptions underlying the binomial distributions are met, find the probability that at most 3 chips fail in a rand
> A continuous random variable X that can assume values between x = 2 and x = 5 has a density function given by f(x) = 2(1 + x)/27. Find (a) P(X
> A continuous random variable X that can assume values between x = 1 and x = 3 has a density function given by f(x) = 1/2. (a) Show that the area under the curve is equal to 1. (b) Find P(2 < X < 2.5). (c) Find P(X ≤ 1.6).
> Construct a graph of the cumulative distribution function of Exercise 3.15.
> Find the cumulative distribution function of the random variable X representing the number of defectives in Exercise 3.11. Then using F(x), find (a) P(X = 1); (b) P(0 < X ≤ 2).
> The waiting time, in hours, between successive speeders spotted by a radar unit is a continuous random variable with cumulative distribution function Find the probability of waiting less than 12 minutes between successive speeders (a) using the cumulat
> The probability distribution of X, the number of imperfections per 10 meters of a synthetic fabric in continuous rolls of uniform width, is given by Construct the cumulative distribution function of X. 1 3 4 f(x) 0.41 0.37 0.16 0.05 0.01
> An investment firm offers its customers municipal bonds that mature after varying numbers of years. Given that the cumulative distribution function of T, the number of years to maturity for a randomly selected bond, is find (a) P(T = 5); (b) P(T > 3)
> A shipment of 7 television sets contains 2 defective sets. A hotel makes a random purchase of 3 of the sets. If x is the number of defective sets purchased by the hotel, find the probability distribution of X. Express the results graphically as a probabi
> A paint-store chain produces and sells latex and semigloss paint. Based on long-range sales, the probability that a customer will purchase latex paint is 0.75. Of those that purchase latex paint, 60% also purchase rollers. But only 30% of semigloss paint
> A regional telephone company operates three identical relay stations at different locations. During a one-year period, the number of malfunctions reported by each station and the causes are shown below. Suppose that a malfunction was reported and it wa
> A safety engineer claims that only 40% of all workers wear safety helmets when they eat lunch at the workplace. Assuming that this claim is right, find the probability that 4 of 6 workers randomly chosen will be wearing their helmets while having lunch a
> Find a formula for the probability distribution of the random variable X representing the outcome when a single die is rolled once.
> Classify the following random variables as discrete or continuous: X: the number of automobile accidents per year in Virginia. Y : the length of time to play 18 holes of golf. M: the amount of milk produced yearly by a particular cow. N: the number of eg
> For the sample space of Exercise 2.5, (a) list the elements corresponding to the event A that a number less than 3 occurs on the die; (b) list the elements corresponding to the event B that two tails occur; (c) list the elements corresponding to the even
> The probability that an automobile being filled with gasoline also needs an oil change is 0.25; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and the filter need changing is 0.14. (a) If the oil has to be c
> For the sample space of Exercise 2.4, (a) list the elements corresponding to the event A that the sum is greater than 8; (b) list the elements corresponding to the event B that a 2 occurs on either die; (c) list the elements corresponding to the event C
> In USA Today (Sept. 5, 1996), the results of a survey involving the use of sleepwear while traveling were listed as follows: (a) What is the probability that a traveler is a female who sleeps in the nude? (b) What is the probability that a traveler is
> A manufacturer of a flu vaccine is concerned about the quality of its flu serum. Batches of serum are processed by three different departments having rejection rates of 0.10, 0.08, and 0.12, respectively. The inspections by the three departments are sequ
> In the senior year of a high school graduating class of 100 students, 42 studied mathematics, 68 studied psychology, 54 studied history, 22 studied both mathematics and history, 25 studied both mathematics and psychology, 7 studied history but neither ma
> In an experiment to study the relationship of hypertension and smoking habits, the following data are collected for 180 individuals: where H and NH in the table stand for Hypertension and Nonhypertension, respectively. If one of these individuals is se
> A random sample of 200 adults are classified below by sex and their level of education attained. If a person is picked at random from this group, find the probability that (a) the person is a male, given that the person has a secondary education; (b) t
> The probabilities are 0.4, 0.2, 0.3, and 0.1, respectively, that a delegate to a certain convention arrived by air, bus, automobile, or train. What is the probability that among 9 delegates randomly selected at this convention, 3 arrived by air, 3 arrive
> A class in advanced physics is composed of 10 juniors, 30 seniors, and 10 graduate students. The final grades show that 3 of the juniors, 10 of the seniors, and 5 of the graduate students received an A for the course. If a student is chosen at random fro
> If R is the event that a convict committed armed robbery and D is the event that the convict pushed dope, state in words what probabilities are expressed by (a) P(R|D); (b) P(D’|R); (c) P(R’|D’).
> Prove that P(A’ ∩ B’) = 1+P(A ∩ B) − P(A) − P(B).
> As the situation of Exercise 2.69 might suggest, statistical procedures are often used for control of quality (i.e., industrial quality control). At times, the weight of a product is an important variable to control. Specifications are given for the weig
> Consider the situation of Exercise 2.69. Suppose 50,000 boxes of detergent are produced per week and suppose also that those underfilled are “sent back,” with customers requesting reimbursement of the purchase price. Suppose also that the cost of product
> Four students are selected at random from a chemistry class and classified as male or female. List the elements of the sample space S1, using the letter M for male and F for female. Define a second sample space S2 where the elements represent the number
> It is common in many industrial areas to use a filling machine to fill boxes full of product. This occurs in the food industry as well as other areas in which the product is used in the home, for example, detergent. These machines are not perfect, and in
> Interest centers around the nature of an oven purchased at a particular department store. It can be either a gas or an electric oven. Consider the decisions made by six distinct customers. (a) Suppose that the probability is 0.40 that at most two of thes
> Consider the situation of Example 2.32 on page 58. (a) What is the probability that no more than 4 cars will be serviced by the mechanic? (b) What is the probability that he will service fewer than 8 cars? (c) What is the probability that he will service
> Factory workers are constantly encouraged to practice zero tolerance when it comes to accidents in factories. Accidents can occur because the working environment or conditions themselves are unsafe. On the other hand, accidents can occur due to carelessn
> According to a genetics theory, a certain cross of guinea pigs will result in red, black, and white offspring in the ratio 8:4:4. Find the probability that among 8 offspring, 5 will be red, 2 black, and 1 white.
> Consider the situation of Exercise 2.64. Let A be the event that the component fails a particular test and B be the event that the component displays strain but does not actually fail. Event A occurs with probability 0.20, and event B occurs with probabi

