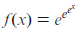Question: Differentiate. /
> The wholesale price in dollars of one pound of ground beef is modeled by the function f (t) = 3.08 + .57t - .1t2 + .01t3, where t is measured in years from January 1, 2010. (a) Estimate the price in 2011 and find the rate in dollars per year at which the
> The price of wheat per bushel at time t (in months) is approximated by f (t) = 4 + .001t + .01e-t. What is the percentage rate of change of f (t) at t = 0? t = 1? t = 2?
> Find the logarithmic derivative and then determine the percentage rate of change of the function at the point indicated. f (t) = t2 at t = 10 and t = 50
> A function h (x) is defined in terms of a differentiable f (x). Find an expression for h (x). h(x) = xf (x)
> Differentiate the following functions. f (x) = -7ex/7
> Differentiate the following functions. f (x) = e√(x2+1)
> Differentiate the following functions. f (x) = e√x
> Differentiate the following functions. f (x) = e1/x
> The amount in grams of a certain radioactive material present after t years is given by the function P(t). Match each of the following answers with its corresponding question. Answers a. Solve P(t) = .5P(0) for t. b. Solve P(t) = .5 for t. c. P(.5) d. P
> The rate of growth of a certain cell culture is proportional to its size. In 10 hours a population of 1 million cells grew to 9 million. How large will the cell culture be after 15 hours?
> Differentiate the following functions. f (x) = eex
> Let f (t) be the function from Exercise 39 that gives the height (inches) of a plant at time t (weeks). (a) When is the plant 11 inches tall? (b) When is the plant growing at the rate of 1 inch per week? (c) What is the fastest rate of growth of the plan
> In a study, a cancerous tumor was found to have a volume of f (t) = 1.8253(1 - 1.6e-0.4196t)3 milliliters after t weeks, with t > 1. (Source: Growth, Development and Aging.) (a) Sketch the graphs of f (t) and f ‘(t) for 1 ≤ t ≤ 15. What do you notice abo
> Find dy/dx if
> Let a and b be positive numbers. A curve whose equation is is called a Gompertz growth curve. These curves are used in biology to describe certain types of population growth. Compute the derivative of / y = e`^ae-box
> The length of a certain weed, in centimeters, after t weeks is f (t) = 6/(.2 + 5e-0.5t). Answer the following questions by reading the graph in Fig. 3. (a) How fast is the weed growing after 10 weeks? (b) When is the weed 10 centimeters long? (c) When is
> Find d2y/dx2. y = x√x + 1
> Differentiate the functions. y = (x2 + x + 1)3(x - 1)4
> Differentiate the following functions. f (x) = e(1+x)3
> The height of a certain plant, in inches, after t weeks is f (t) = 1/(.05 + e-0.4t). The graph of f (t) resembles the graph in Fig. 3. Calculate the rate of growth of the plant after 7 weeks. Figure 3: 30%/- 20 10 400 y=f"(1) 6.4 y=f(t) y = f'(0) 1
> Let T be the time constant of the curve y = Ce-λt as defined in Fig. 5. Show that T = 1>λ.
> Suppose that the velocity of a parachutist is υ(t) = 65(1 - e-0.16t) meters per second. The graph of υ(t) is similar to that in Fig. 2. Calculate the parachutist’s velocity and acceleration when t = 9 seconds. Fig
> The velocity of a parachutist during free fall is f (t) = 60(1 - e-0.17t) meters per second. Answer the following questions by reading the graph in Fig. 2. (Recall that acceleration is the derivative of velocity.) (a) What is the velocity when t = 8 seco
> A painting purchased in 2015 for $100,000 is estimated to be worth υ(t) = 100,000et/5 dollars after t years. At what rate will the painting be appreciating in 2020?
> The highest price ever paid for an artwork at auction was for Pablo Picasso’s 1955 painting Les femmes d’Alger, which fetched $179.4 million in a Christie’s auction in 2015. The painting was last sold in 1997 for $31.9 million. If the painting keeps on a
> The value of a computer t years after purchase is υ(t) = 2000e-0.35t dollars. At what rate is the computer’s value falling after 3-years?
> The value of an investment portfolio consisting of two stocks is given by f (t) = 3e0.06t + 2e0.02t, where t is the number of years since the inception of the portfolio, and f (t) is in thousands of dollars. (a) What is the initial dollar amount invested
> Find the values of x at which the function has a possible relative maximum or minimum point. (Recall that ex is positive for all x.) Use the second derivative to determine the nature of the function at these points. f (x) = (2x - 5)e3x-1
> Find the values of x at which the function has a possible relative maximum or minimum point. (Recall that ex is positive for all x.) Use the second derivative to determine the nature of the function at these points. f (x) = (5x - 2)e1-2x
> Find d2y/dx2. y = x√x + 1
> Find the values of x at which the function has a possible relative maximum or minimum point. (Recall that ex is positive for all x.) Use the second derivative to determine the nature of the function at these points. f (x) = (4x – 1)/ex/2
> Many scientists believe there have been four ice ages in the past 1 million years. Before the technique of carbon dating was known, geologists erroneously believed that the retreat of the Fourth Ice Age began about 25,000 years ago. In 1950, logs from an
> Differentiate the following functions. f (x) = e4x2-x
> Find the values of x at which the function has a possible relative maximum or minimum point. (Recall that ex is positive for all x.) Use the second derivative to determine the nature of the function at these points. f (x) = (3 - 4x)/e2x
> Find the values of x at which the function has a possible relative maximum or minimum point. (Recall that ex is positive for all x.) Use the second derivative to determine the nature of the function at these points. f (x) = (1 - x)e2x
> Find the values of x at which the function has a possible relative maximum or minimum point. (Recall that ex is positive for all x.) Use the second derivative to determine the nature of the function at these points. f (x) = (1 + x)e-3x
> Simplify the function before differentiating. f (t) = √(e3x)
> Simplify the function before differentiating. f (x) = (ex + 5e2x)/ex
> Simplify the function before differentiating. f (t) = e3t(e2t - e4t)
> Simplify the function before differentiating. f (x) = 1/√ex
> Simplify the function before differentiating. f (x) = exe2xe3x
> Find d2y/dx2. y = √ (x2 + 1)
> In 1938, sandals woven from strands of tree bark were found in Fort Rock Creek Cave in Oregon. The bark contained 34% of the level of 14C found in living bark. Approximately how old were the sandals?
> Simplify the function before differentiating. f (x) = (e3x)5
> Differentiate. f (x) = eex
> Differentiate the following functions. f (x) = e-3x-2
> Differentiate. f (x) = √(ex + 1)
> Differentiate. f (x) = (ex - e-x)/(ex + e-x)
> Differentiate. f (x) = (ex + e-x)/(ex - e-x)
> Differentiate. f (x) = (x + 1/x)e2x
> Differentiate. f (t) = (t3 - 3t)e1+t
> Differentiate. f (t) = (t2 + 2et)et-1
> Differentiate the functions. y = x4 + 4 4√x
> Find d2y/dx2. y = (x2 + 1)4
> Differentiate. f (t) = 2et/2 - .4e0.001 t
> Differentiate. f (t) = 4e0.05t - 23e0.01t
> Differentiate the following functions. f (x) = 10e(-x – 2)/5
> Differentiate the following functions. f (x) = e2x+3
> A motorcyclist is driving over a ramp as shown in Fig. 10 at the speed of 80 miles per hour. How fast is she rising? Figure 10: x 1000 ft h 100 ft
> A baseball diamond is a 90-foot by 90-foot square. (See Fig. 9.) A player runs from first to second base at the speed of 22 feet per second. How fast is the player’s distance from third base changing when he is halfway between first and
> An airplane flying 390 feet per second at an altitude of 5000 feet flew directly over an observer. Figure 8 shows the relationship of the airplane to the observer at a later time. (a) Find an equation relating x and y. (b) Find the value of x when y is 1
> Figure 7 shows a 10-foot ladder leaning against a wall. (a) Use the Pythagorean theorem to find an equation relating x and y. (b) If the foot of the ladder is being pulled along the ground at the rate of 3 feet per second, how fast is the top end of the
> Suppose that in Boston the wholesale price, p, of oranges (in dollars per crate) and the daily supply, x (in thousands of crates), are related by the equation px + 7x + 8p = 328. If there are 4 thousand crates available today at a price of $25 per crate,
> Determine the growth constant k, then find all solutions of the given differential equation. y' – y/2 = 0
> The monthly advertising revenue, A, and the monthly circulation, x, of a magazine are related approximately by the equation A = 6 √(x2 – 400), x ≥ 20, where A is given in thousands of dollars and x is measured in thousands of copies sold. At what rate
> Find the point(s) on the graph of y = (2x4 + 1)(x - 5) where the slope is 1.
> Suppose that the price p (in dollars) and the weekly demand, x (in thousands of units) of a commodity satisfy the demand equation 6p + x + xp = 94. How fast is the demand changing at a time when x = 4, p = 9, and the price is rising at the rate of $2 p
> Suppose that the price p (in dollars) and the weekly sales x (in thousands of units) of a certain commodity satisfy the demand equation 2p3 + x2 = 4500. Determine the rate at which sales are changing at a time when x = 50, p = 10, and the price is falli
> A point is moving along the graph of x3y2 = 200. When the point is at (2, 5), its x-coordinate is changing at the rate of -4 units per minute. How fast is the y-coordinate changing at that moment?
> A point is moving along the graph of x2 - 4y2 = 9. When the point is at (5, -2), its x-coordinate is increasing at the rate of 3 units per second. How fast is the y-coordinate changing at that moment?
> Suppose that x and y are both differentiable functions of t and are related by the given equation. Use implicit differentiation with respect to t to determine dy/dt in terms of x, y, and dx/dt. x2y2 = 2y3 + 1
> Suppose that x and y are both differentiable functions of t and are related by the given equation. Use implicit differentiation with respect to t to determine dy/dt in terms of x, y, and dx/dt. x2 + 2xy = y3
> Suppose that x and y are both differentiable functions of t and are related by the given equation. Use implicit differentiation with respect to t to determine dy/dt in terms of x, y, and dx/dt. y2 = 8 + xy
> Suppose that x and y are both differentiable functions of t and are related by the given equation. Use implicit differentiation with respect to t to determine dy/dt in terms of x, y, and dx/dt. 3xy - 3x2 = 4
> A 4500-year-old wooden chest was found in the tomb of the twenty-fifth century b.c. Chaldean king Meskalumdug of Ur. What percentage of the original 14C would you expect to find in the wooden chest?
> Suppose that x and y are both differentiable functions of t and are related by the given equation. Use implicit differentiation with respect to t to determine dy/dt in terms of x, y, and dx/dt. y4 - x2 = 1
> Suppose that x and y are both differentiable functions of t and are related by the given equation. Use implicit differentiation with respect to t to determine dy/dt in terms of x, y, and dx/dt. x4 + y4 = 1
> Find the point(s) on the graph of y = (x2 + 3x - 1)/x where the slope is 5.
> Suppose that x and y represent the amounts of two basic inputs for a production process and 10x1/2y1/2 = 600. Find dy/dx when x = 50 and y = 72.
> Suppose that x and y represent the amounts of two basic inputs for a production process and that the equation 30x1/3y2/3 = 1080 describes all input amounts where the output of the process is 1080 units. (a) Find dy/dx. (b) What is the marginal rate of
> The graph of x4 + 2x2y2 + y4 = 9x2 - 9y2 is a lemniscate similar to that in Fig. 6. (a) Find dy/dx by implicit differentiation. (b) Find the slope of the tangent line to the lemniscate at (√5, -1). Figure 6: У (x² + y²2 = 4x² - 4у
> The graph of x4 + 2x2y2 + y4 = 4x2 - 4y2 is the lemniscate in Fig. 6. (a) Find dy/dx by implicit differentiation. (b) Find the slope of the tangent line to the lemniscate at (√6/2, √2/2). Figure 6: У (x² + y²2 =
> Find the equation of the tangent line to the graph of x4 y2 = 144 at the point (2, 3) and at the point (2, -3).
> Find the equation of the tangent line to the graph of x2 y4 = 1 at the point (4, 12) and at the point (4, - 12 ).
> Use implicit differentiation of the equation to determine the slope of the graph at the given point. y2 = 3xy - 5; x = 2, y = 1
> According to legend, in the fifth century King Arthur and his knights sat at a huge round table. A round table alleged to have belonged to King Arthur was found at Winchester Castle in England. In 1976, carbon dating revealed the amount of radiocarbon in
> Use implicit differentiation of the equation to determine the slope of the graph at the given point. xy + y3 = 14; x = 3, y = 2
> Use implicit differentiation of the equation to determine the slope of the graph at the given point. √x + √y = 7; x = 9, y = 16
> Use implicit differentiation of the equation to determine the slope of the graph at the given point. xy3 = 2; x = - 14, y = -2
> The graph of y = (x2 - 1)4 (x2 + 1)5 is shown in Fig. 3. Find the coordinates of the local maxima and minima. Figure 3: -1 김 1 y = r2 - 1)(G2 + 1) 1
> Use implicit differentiation of the equation to determine the slope of the graph at the given point. y2 = x3 + 1; x = 2, y = -3
> Use implicit differentiation of the equation to determine the slope of the graph at the given point. 4y3 - x2 = -5; x = 3, y = 1
> Suppose that x and y are related by the given equation and use implicit differentiation to determine dy/dx. x3y + xy3 = 4
> Suppose that x and y are related by the given equation and use implicit differentiation to determine dy/dx. x2y + y2x = 3
> Suppose that x and y are related by the given equation and use implicit differentiation to determine dy/dx. x2 + 4xy + 4y = 1
> Suppose that x and y are related by the given equation and use implicit differentiation to determine dy/dx. x3 + y3 = x3y3
> In 1947, a cave with beautiful prehistoric wall paintings was discovered in Lascaux, France. Some charcoal found in the cave contained 20% of the 14C expected in living trees. How old are the Lascaux cave paintings? (Recall that the decay constant for 14
> Suppose that x and y are related by the given equation and use implicit differentiation to determine dy/dx. (x + 1)2 (y - 1)2 = 1
> Suppose that x and y are related by the given equation and use implicit differentiation to determine dy/dx. x3y2 - 4x2 = 1
> Suppose that x and y are related by the given equation and use implicit differentiation to determine dy/dx. x2y3 = 6