Question: Find an equation of the tangent plane
Find an equation of the tangent plane to the given parametric surface at the specified point. Graph the surface and the tangent plane.
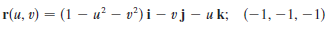
Transcribed Image Text:
r(u, v) = (1 – u² – v²) i – vj – u k; (-1, –1, –1)
> Match the vector fields F on R3 with the plots labeled I–IV. Give reasons for your choices. F (x, y, z) = i + 2 j + z k II 1- -1 -1 0 y
> Match the vector fields F on R3 with the plots labeled I–IV. Give reasons for your choices. F (x, y, z) = i + 2 j + 3 k 1 z0- -1 -1 0 1 10-1 y
> Match the vector fields F with the plots labeled I–IV. Give reasons for your choices. F (x, y) = 〈cos (x + y), x〉 IV 3 -3 3 11 -3
> Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. Figure 9: F (x, y) = (yi + xj)/√ (x^2+y^2) ZA
> If z is defined implicitly as a function of x and y by an equation of the form F (x, y, z) = 0, how do you find ∂zy/∂x and ∂z/∂y?
> If z = f (x, y), what are the differentials dx, dy, and dz?
> Evaluate the line integral, where C is the given curve. ∫C x2y ds, C: x = cos t, y = sin t, z = t, 0 < t < π/2
> If the components of F have continuous second partial derivatives and S is the boundary surface of a simple solid region, show that ∫∫S curl F ∙ dS = 0.
> Investigate the shape of the surface with parametric equations x = sin u, y = sin v, z = sin (u + v). Start by graphing the surface from several points of view. Explain the appearance of the graphs by determining the traces in the horizontal planes z = 0
> Evaluate the line integral, where C is the given curve. ∫C x2 dx + y2 dy, C consists of the arc of the circle x2 + y2 = 4 from (2, 0) to (0, 2) followed by the line segment from (0, 2) to (4, 3)
> Evaluate the line integral, where C is the given curve. ∫C (x + 2y) dx + x2 dy, C consists of line segments from (0, 0) to (2, 1) and from (2, 1) to (3, 0)
> Evaluate the line integral, where C is the given curve. ∫C ex dx, C is the arc of the curve x = y3 from (-1, -1) to (1, 1)
> Evaluate the line integral, where C is the given curve. ∫C (x2y + sin x) dy, C is the arc of the parabola y = x2 from (0, 0) to (π, π2)
> Evaluate the line integral, where C is the given curve. ∫C xey ds, C is the line segment from (2, 0) to (5, 4)
> A thin wire is bent into the shape of a semicircle x2 + y2 = 4, x > 0. If the linear density is a constant k, find the mass and center of mass of the wire.
> Find the exact value of ∫C x3y2z ds, where C is the curve with parametric equations x = e-t cos 4t, y = e-t sin 4t, z = e-t, 0 < t < 2 π.
> (a). Evaluate the line integral∫C F ∙ dr, where F (x, y, z) = x i - z j + y k and C is given by r(t) = 2t i + 3t j - t2 k, -1 (b). Illustrate part (a) by using a computer to graph C and the vectors from the vector fie
> Evaluate the line integral, where C is the given curve. ∫C xy4 ds, C is the right half of the circle x2 + y2 = 16
> Use a calculator to evaluate the line integral correct to four decimal places. ∫C z ln (x + y) ds, where C has parametric equations x = 1 + 3t, y = 2 + t2, z = t4, -1 < t < 1
> Find ∫∫S F ∙ n dS, where F (x, y, z) = x i + y j + z k and S is the outwardly oriented surface shown in the figure (the boundary surface of a cube with a unit corner cube removed). ZA (0, 2, 2)
> Use a calculator to evaluate the line integral correct to four decimal places. ∫C xy arctan z ds, where C has parametric equations x = t2, y = t3, z = √t, 1 < t < 2
> (a). Find a parametric representation for the torus obtained by rotating about the z-axis the circle in the xz-plane with center (b, 0, 0) and radius a (b). Use the parametric equations found in part (a) to graph the torus for several values of a and b.
> Use a calculator to evaluate the line integral correct to four decimal places. ∫C F ∙ dr, where F (x, y) = √(x + y) i + (y/x) j and r(t) = sin2 t i + sin t cos t j, π/6 < t < π/3
> Evaluate the line integral ∫C F ∙ dr, where C is given by the vector function r(t). F (x, y, z) = x i + y j + xy k, r(t) = cos t i + sin t j + t k, 0 < t < π
> Evaluate the line integral ∫C F ∙ dr, where C is given by the vector function r(t). F (x, y, z) = sin x i + cos y j + xz k, r (t) = t3 i - t2 j + t k, 0 < t < 1
> (a). Show that the parametric equations x = a cosh u cos v, y = b cosh u sin v, z = c sinh u, represent a hyperboloid of one sheet. (b). Use the parametric equations in part (a) to graph the hyperboloid for the case a = 1, b = 2, c = 3. (c). Set up, but
> Evaluate the line integral, where C is the given curve. ∫C (x/y) ds, C: x = t 3, y = t 4, 1 < t < 2
> Evaluate the line integral ∫C F ∙ dr, where C is given by the vector function r(t). F (x, y) = xy2 i - x2 j, r(t) = t3 i + t2 j, 0 < t < 1
> Find the exact area of the surface z = 1 + 2x + 3y + 4y2, 1 < x < 4, 0 < y < 1.
> Find the area of the surface with vector equation r (u, v) = 〈cos3u cos3v, sin3u cos3v, sin3v〉, 0 < u < u, 0 < v < 2π. State your answer corrects to four decimal places.
> Let F (x, y) = (2x3 + 2xy2 - 2y) i + (2y3 + 2x2y + 2x) j x2 + y2 Evaluate ∫C F ∙ dr, where C is shown in the figure. C
> (a). Use the Midpoint Rule for double integrals (see Section 15.1) with six squares to estimate the area of the surface z = 1/ (1 + x2 + y2), 0 < x < 6, 0 < y < 4. (b). Use a computer algebra system to approximate the surface area in part (a) to four dec
> Find, to four decimal places, the area of the part of the surface z = (1 + x2)/ (1 + y2) that lies above the square |x | + |y | < 1. Illustrate by graphing this part of the surface.
> Find the area of the surface correct to four decimal places by expressing the area in terms of a single integral and using your calculator to estimate the integral. The part of the surface z = ln (x2 + y2 + 2) that lies above the disk x2 + y2 < 1
> Find the area of the surface correct to four decimal places by expressing the area in terms of a single integral and using your calculator to estimate the integral. The part of the surface z = cos (x2 + y2) that lies inside the cylinder x2 + y2 = 1
> If the equation of a surface S is z = f (x, y), where x2 + y2 < R2, and you know that | fx | < 1 and | fy | < 1, what can you say about A (S)?
> If C is a smooth curve given by a vector function r (t), a r• dr = {[Ir(b)|? – \r(a)F]
> Let F be an inverse square field, that is, F (r) = cr/|r |3 for some constant c, where r = x i + y j + z k. Show that the flux of F across a sphere S with center the origin is independent of the radius of S.
> The temperature at a point in a ball with conductivity K is inversely proportional to the distance from the center of the ball. Find the rate of heat flow across a sphere S of radius a with center at the center of the ball.
> The temperature at the point (x, y, z) in a substance with conductivity K = 6.5 is u (x, y, z) = 2y2 + 2z2. Find the rate of heat flow inward across the cylindrical surface y2 + z2 = 6, 0 < x < 4.
> Use Gauss’s Law to find the charge enclosed by the cube with vertices (±1, ±1, ±1) if the electric field is E (x, y, z) = x i + y j + z k
> Let F (x, y, z) = (3x2yz - 3y) i + (x3z - 3x) j + (x3y + 2z) k Evaluate ∫C F ∙ dr, where C is the curve with initial point (0, 0, 2) and terminal point (0, 3, 0) shown in the figure. ZA (0, 0, 2) (0, 3, 0) (1, 1,
> Use Gauss’s Law to find the charge contained in the solid hemisphere x2 + y2 + z2 < a2, z > 0, if the electric field is E (x, y, z) = x i + y j + 2z k
> Seawater has density 1025 kg/m3 and flows in a velocity field v = y i + x j, where x, y, and z are measured in meters and the components of v in meters per second. Find the rate of flow outward through the hemisphere x2 + y2 + z2 = 9, z > 0.
> A fluid has density 870 kg/m3 and flows with velocity v = z i + y2 j + x2 k, where x, y, and z are measured in meters and the components of v in meters per second. Find the rate of flow outward through the cylinder x2 + y2 = 4, 0 < z < 1.
> Find the area of the surface. The part of the cone z = √x2 + y2 that lies between the plane y = x and the cylinder y = x2
> (a). Give an integral expression for the moment of inertia Iz about the z-axis of a thin sheet in the shape of a surface S if the density function is ρ. (b). Find the moment of inertia about the z-axis of the funnel in Exercise 40 Exercise 40: Find the
> Find the mass of a thin funnel in the shape of a cone z = √x2 + y2, 1 < z < 4, if its density function is ρ (x, y, z) = 10 - z.
> Find the center of mass of the hemisphere x2 + y2 + z2 = a2, z > 0, if it has constant density.
> Find an equation of the tangent plane to the given parametric surface at the specified point. Graph the surface and the tangent plane. r(u, v) = ưi + 2u sin vj + u cos vk; u = 1, v =0
> Find the flux of F (x, y, z) = sin (xyz) i + x2y j + z2ex/5 k across the part of the cylinder 4y2 + z2 = 4 that lies above the xy-plane and between the planes x = -2 and x = 2 with upward orientation. Illustrate by using a computer algebra system to draw
> Compute the outward flux of F (x, y, z) = x i + y j + z k/ (x2 + y2 + z2)3/2 through the ellipsoid 4x2 + 9y2 + 6z2 = 36.
> Find the value of ∫∫S x2y2z2 dS correct to four decimal places, where S is the part of the paraboloid z = 3 - 2x2 - y2 that lies above the xy-plane.
> Find the exact value of ∫∫S xyz dS, where S is the surface z = x2y2, 0 < x < 1, 0 < y < 2.
> Evaluate ∫∫S (x2 + y2 + z2) dS correct to four decimal places, where S is the surface z = xey, 0 < x < 1, 0 < y < 1.
> The surface with parametric equations x = 2 cos θ + r cos (θ /2) y = 2 sin θ + r cos (θ /2) z = r sins (θ /2) where -1/2 < r < 12 and 0
> Suppose S and E satisfy the conditions of the Divergence Theorem and f is a scalar function with continuous partial derivatives. Prove that These surface and triple integrals of vector functions are vectors defined by integrating each component functio
> Prove each identity, assuming that S and E satisfy the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second-order partial derivatives. (SVg – gVf) •n ds = [[[ (fV²g – gV²f) aV E
> Solve the boundary-value problem, if possible. y'' = y', y (0) = 1, y (1) = 2
> Solve the differential equation using the method of variation of parameters. y'' + 4y' + 4y = e-2x/x3
> Solve the differential equation using the method of variation of parameters. y'' – y' + y = ex/1 + x2
> Solve the differential equation using the method of variation of parameters. y'' + 3y' + 2y = sin (ex)
> Verify that the Divergence Theorem is true for the vector field F (x, y, z) = x i + y j + z k, where E is the unit ball x2 + y2 + z2 < 1.
> Solve the differential equation using the method of variation of parameters. y'' - 3y' + 2y = 1/1 + e-x
> Solve the differential equation using the method of variation of parameters. y'' + y = sec3x, 0 < x < π/2
> Solve the differential equation using the method of variation of parameters. y'' + y = sec2x, 0 < x < π/2
> Plot the vector field and guess where div F > 0 and where div F F(x, y) = (x², y²)
> Evaluate the surface integral ∫∫S F ∙ dS for the given vector field F and the oriented surface S. In other words, find the flux of F across S. For closed surfaces, use the positive (outward) orientation. F (x, y, z) = zexy i - 3zexy j + xy k, S is the p
> Solve the differential equation using (a) undetermined coefficients and (b) variation of parameters. у" — 2у' — Зу %3х+2 3y = x + 2
> Solve the differential equation using (a) undetermined coefficients and (b) variation of parameters. 4y" + у %3 сos x
> Write a trial solution for the method of undetermined coefficients. Do not determine the coefficients. y" + 4y = ex + x sin 2.x
> Verify that the solution to Equation 1 can be written in the form x (t) = A cos (ω t + δ).
> The battery in Exercise 14 is replaced by a generator producing a voltage of E (t) = 12 sin 10t. Exercise 14: A series circuit contains a resistor with R = 24 V, an inductor with L = 2 H, a capacitor with C = 0.005 F, and a 12-V battery. (a). Find the
> Use the Divergence Theorem to calculate the surface integral ∫∫S F ∙ dS, where F (x, y, z) = x3 i + y3 j + z3 k and S is the surface of the solid bounded by the cylinder x2 + y2 = 1 and the planes z = 0 and z = 2.
> The battery in Exercise 13 is replaced by a generator producing a voltage of E (t) = 12 sin 10t. Find the charge at time t. Exercise 13: A series circuit consists of a resistor with R = 20 V, an inductor with L = 1 H, a capacitor with C = 0.002 F, and
> A series circuit contains a resistor with R = 24 V, an inductor with L = 2 H, a capacitor with C = 0.005 F, and a 12-V battery. The initial charge is Q = 0.001 C and the initial current is 0. (a). Find the charge and current at time t. (b). Graph the cha
> A series circuit consists of a resistor with R = 20 V, an inductor with L = 1 H, a capacitor with C = 0.002 F, and a 12-V battery. If the initial charge and current are both 0, find the charge and current at time t.
> The solution of the initial-value problem x2y'' + xy' + x2y = 0 y (0) = 1 y' (0) = 0 is called a Bessel function of order 0. (a). Solve the initial-value problem to find a power series expansion for the Bessel function. (b). Graph several Taylor polynomi
> Use power series to solve the differential equation. y'' + x2y' + xy = 0, y (0) = 0, y' (0) = 1
> Use power series to solve the differential equation. y'' + x2y = 0, y (0) = 1, y'(0) = 0
> Use power series to solve the differential equation. y'' – xy' - y = 0, y (0) = 1, y' (0) = 0
> Use power series to solve the differential equation. y'' = xy
> Use power series to solve the differential equation. (x – 1) y' + y' = 0
> Use power series to solve the differential equation. y'' = y
> Use Stokes’ Theorem to evaluate ∫C F ∙ dr, where F (x, y, z) = xy i + yz j + z x k, and C is the triangle with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1), oriented counterclockwise as viewed from above.
> Use power series to solve the differential equation. y'' + xy' + y = 0
> Use power series to solve the differential equation. (x – 3) y' + 2y = 0
> Use power series to solve the differential equation. y' = x2y
> Solve the differential equation. Y'' - 6y' + 9y = 0
> Use power series to solve the differential equation. y' – y = 0
> How do you find the cross product a × b of two vectors if you know their lengths and the angle between them? What if you know their components?
> Write expressions for the scalar and vector projections of b onto a. Illustrate with diagrams.
> How do you find the dot product a ∙ b of two vectors if you know their lengths and the angle between them? What if you know their components?
> How do you find the vector from one point to another?
> How do you add two vectors geometrically? How do you add them algebraically?
> Use Stokes’ Theorem to evaluate ∫∫S curl F ∙ dS, where F (x, y, z) = x2yz i + yz2 j + z3exy k, S is the part of the sphere x2 + y2 + z2 = 5 that lies above the plane z = 1, and S is oriented upward.
> Write equations in standard form of the six types of quadric surfaces.
> How do you find the angle between two intersecting planes?
> (a). How do you find the area of the parallelogram determined by a and b? (b). How do you find the volume of the parallelepiped determined by a, b, and c?
> What is the difference between a vector and a scalar?

