Question: Find the area of the region that
Find the area of the region that lies inside the first curve and outside the second curve.
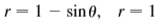
Transcribed Image Text:
r = 1 - sin0, r= 1
> Find the points on the given curve where the tangent line is horizontal or vertical. r=1+ cos 0
> Find the points on the given curve where the tangent line is horizontal or vertical. r=1- sin 0
> Find the points on the given curve where the tangent line is horizontal or vertical. -r= 3 cos 0
> Determine whether the series is absolutely convergent or conditionally convergent. (-1)* -1 In
> Match the polar equations with the graphs labeled I–VI. Give reasons for your choices. (Don’t use a graphing device.) (a) r= In 0, 1 < 0 < 6 (c) r= cos 30 (e) r= cos(0/2) (b) r= 0°, 0< 0 < 87 (d) r=2 + cos 30 (f)
> Sketch the curve (x2 + y2)3 = 4x2y2
> Test the series for convergence or divergence. E (v2 – 1)
> For each of the described curves, decide if the curve would be more easily given by a polar equation or a Cartesian equation. Then write an equation for the curve. (a) A circle with radius 5 and center (2, 3) (b) A circle centered at the origin with radi
> Find a polar equation for the curve represented by the given Cartesian equation. x? + y? = 2cx CX
> Find a polar equation for the curve represented by the given Cartesian equation. 4y2
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. (-1)* arctan n Σ n2
> Use a computer algebra system to find the Taylor polynomials Tn centered at a for n = 2, 3, 4, 5. Then graph these polynomials and f on the same screen. f(x) = V1 + x², a=0 %3D
> Find a polar equation for the curve represented by the given Cartesian equation. y = 1 + 3x
> Identify the curve by finding a Cartesian equation for the curve. r= 5 cos 0
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r > 1, T< 0 < 2
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. 2 <r< 3, 57/3 < 0 < 7m/3
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. 1<r<3, п/6 <0 < 5п/6
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r> 0, T/4 < 0 < 37/4
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. () < r < 2, T<0 < 37/2
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r> 1
> Test the series for convergence or divergence. 1 (In n)n -2
> Plot the point whose polar coordinates are given. Then find the Cartesian coordinates of the point. (а) (4,4п/3) (b) (-2, Зп/4) (е) (-3, — п/3)
> Plot the point whose polar coordinates are given. Then find the Cartesian coordinates of the point. (а) (2, 3п/2) () (/2, т/4) (c) (-1, — п/6)
> Plot the point whose polar coordinates are given. Then find two other pairs of polar coordinates of this point, one with r > 0 and one with r (a) (2, 5п/6) (b) (1, —2т/3) (е) (-1,5п/4)
> (a) Find a formula for the area of the surface generated by rotating the polar curve / / about the line / (b) Find the surface area generated by rotating the lemniscate r = f(0), a < 0 < b (where f' is
> Use a calculator to find the length of the curve correct to four decimal places. If necessary, graph the curve to determine the parameter interval. r = sin(0/4)
> Use a calculator to find the length of the curve correct to four decimal places. If necessary, graph the curve to determine the parameter interval. r= sin(6 sin 0)
> Use a calculator to find the length of the curve correct to four decimal places. If necessary, graph the curve to determine the parameter interval. One loop of the curve r = cos 20
> Test the series for convergence or divergence. 1 Σ 1+1/n
> Find the exact length of the curve. Use a graph to determine the parameter interval. r= cos'(0/2)
> Find the exact length of the curve. Use a graph to determine the parameter interval. r = cos (0/4)
> Find the exact length of the polar curve. r= 2(1 + cos 0)
> Find the exact length of the polar curve. r= 0', 0< 0 < 27
> Find the exact length of the polar curve. r= 5°, 0 < 0 < 27
> Find the exact length of the polar curve. r = 2 cos 0, 0 < 0 <
> Test the series for convergence or divergence. 1 Σ n-1 n +n cos'n
> Find the area between a large loop and the enclosed small loop of the curve /
> Find the area inside the larger loop and outside the smaller loop of the limaçon /
> Find the area of the region that lies inside both curves. r = a sin 0, r = b cos 0, a > 0, b > 0
> Find the area of the region that lies inside both curves. r2 - 2 sin 20, r=1
> Find the area of the region that lies inside both curves. r = 3 + 2 cos 0, r= 3 + 2 sin0
> Find the area of the region that lies inside both curves. r = sin 20, r= cos 20
> Test the series for convergence or divergence. n Σ n +
> Find the area of the region that lies inside both curves. r= 1 + cos 0, r=1- cos 0
> Find the area of the region that lies inside both curves. r= 3 sin 0, r= 3 cos
> Find the area of the region that lies inside the first curve and outside the second curve. r = 3 sin 0, r= 2 – sin0
> Find the area of the region that lies inside the first curve and outside the second curve. r= 3 cos 0, r=1+ cos 0
> Find the area of the region that lies inside the first curve and outside the second curve. r = 1 + cos 0, r=2 – cos 0
> Find the area of the region that lies inside the first curve and outside the second curve. r? = 8 cos 20, r=2 %3D
> Find the area of the region that lies inside the first curve and outside the second curve. r = 4 sin 0, r= 2
> Test the series for convergence or divergence. (n!)" Σ 4n n-1
> Graph the curve and find the area that it encloses. r = 2 + sin 40
> Test the series for convergence or divergence. 5* Σ 3* + 4* k-1
> Find the area of the shaded region. r= /In 0, 1< 0<27
> Find the area of the shaded region. r = 4 + 3 sin 0
> Find the area of the shaded region. r=2 + cos 0
> Find the area of the shaded region. r? = sin 20
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r = 1/0, 7/2 <0 < 2m
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r = sin 0 + cos 0, 0 < 0 < T
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r= cos 0, 0 <0 </6
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r = e 0/4, T/2 < 0 <
> Test the series for convergence or divergence. E(-1)' j+ 5 j-1
> (a) Calculate the surface area of the ellipsoid that is generated by rotating an ellipse about its major axis. (b) What is the surface area if the ellipse is rotated about its minor axis?
> Find the centroid of the region enclosed by the x-axis and the top half of the ellipse 9x2 + 4y2 = 36.
> (a) If an ellipse is rotated about its major axis, find the volume of the resulting solid. (b) If it is rotated about its minor axis, find the resulting volume.
> Find the area of the region enclosed by the hyperbola x2/a2 - y2/b2 = 1 and the vertical line through a focus.
> The dwarf planet Pluto travels in an elliptical orbit around the sun (at one focus). The length of the major axis is 1.18 × 1010 km and the length of the minor axis is 1.14 × 1010 km. Use Simpson’s Rule with n = 10 to estimate the distance traveled by th
> Use parametric equations and Simpson’s Rule with n = 8 to estimate the circumference of the ellipse /
> Show that if an ellipse and a hyperbola have the same foci, then their tangent lines at each point of intersection are perpendicular.
> Show that the tangent lines to the parabola x2 = 4py drawn from any point on the directrix are perpendicular.
> Test the series for convergence or divergence. (-1)" n-1 cosh n
> (a) Show that the equation of the tangent line to the parabola y2 = 4px at the point (x0, y0) can be written as (b) What is the x-intercept of this tangent line? Use this fact to draw the tangent line. Уoу — 2p(х + хо)
> Determine the type of curve represented by the equation in each of the following cases: (d) Show that all the curves in parts (a) and (b) have the same foci, no matter what the value of k is. y² = 1 k'k – 16 (a) k> 16 (b) ) < k< 16 (c) k < 0
> Find an equation for the ellipse with foci (1, 1) and (21, 21) and major axis of length 4.
> Show that the function defined by the upper branch of the hyperbola y2/a2 - x2/b2 = 1 is concave upward.
> Use the definition of a hyperbola to derive Equation 6 for a hyperbola with foci (±c, 0) and vertices (±a, 0).
> The LORAN (LOng RAnge Navigation) radio navigation system was widely used until the 1990s when it was superseded by the GPS system. In the LORAN system, two radio stations located at A and B transmit simultaneous signals to a ship or an aircraft located
> A cross-section of a parabolic reflector is shown in the figure. The bulb is located at the focus and the opening at the focus is 10 cm. (a) Find an equation of the parabola. (b) Find the diameter of the opening |CD|, 11 cm from the vertex. C A 5 cm
> The point in a lunar orbit nearest the surface of the moon is called perilune and the point farthest from the surface is called apolune. The Apollo 11 spacecraft was placed in an elliptical lunar orbit with perilune altitude 110 km and apolune altitude 3
> Find an equation for the conic that satisfies the given conditions. Hyperbola, foci (2, 0), (2, 8), asymptotes y = 3 + }x and y = 5 – x
> Find an equation for the conic that satisfies the given conditions. Hyperbola, vertices (±3, 0), asymptotes y = ±2x
> Test the series for convergence or divergence. 1/n .2
> Find an equation for the conic that satisfies the given conditions. Нуperbola, vertices (— 1, 2), (7, 2), foci (-2, 2), (8, 2)
> Find an equation for the conic that satisfies the given conditions. Нурerbola, vertices (-3, —4), (-3, 6), foci (-3, –7), (-3, 9)
> Find an equation for the conic that satisfies the given conditions. Hyperbola, vertices (0, ±2), foci (0, ±5)
> Find an equation for the conic that satisfies the given conditions. Hyperbola, vertices (±3, 0), foci (±5, 0)
> Find an equation for the conic that satisfies the given conditions. Ellipse, foci (+4, 0), passing through (-4, 1.8)
> Find an equation for the conic that satisfies the given conditions. Ellipse, center (-1,4), vertex (-1, 0), focus (-1,6)
> Find an equation for the conic that satisfies the given conditions. Ellipse, foci (0, –1), (8, – 1), vertex (9, – 1)
> Find an equation for the conic that satisfies the given conditions. Ellipse, foci (0, 2), (0, 6), vertices (0, 0), (0, 8)
> Find an equation for the conic that satisfies the given conditions. Ellipse, foci (0, ±/2), vertices (0, ±2)
> Find an equation for the conic that satisfies the given conditions. Ellipse, foci (±2, 0), vertices (±5, 0)
> Test the series for convergence or divergence. k In k (k + 1)° k-1 3
> Use a computer algebra system to find the Taylor polynomials Tn centered at a for n = 2, 3, 4, 5. Then graph these polynomials and f on the same screen. f(x) — сot x, а—п/4
> Find an equation for the conic that satisfies the given conditions. Parabola, vertical axis, passing through (0, 4), (1, 3), and (-2, –6)
> Find an equation for the conic that satisfies the given conditions. Parabola, vertex (3, – 1), horizontal axis, passing through (-15, 2)
> Find an equation for the conic that satisfies the given conditions. Parabola, focus (2, – 1), vertex (2, 3)
> Find an equation for the conic that satisfies the given conditions. Parabola, focus (-4, 0), directrix x 2
> Find an equation for the conic that satisfies the given conditions. Parabola, focus (0, 0), directrix y = 6
> Identify the type of conic section whose equation is given and find the vertices and foci. x? – 2x + 2y? – 8y + 7=0

