Question: Find a polar equation for the curve
Find a polar equation for the curve represented by the given Cartesian equation.
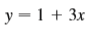
Transcribed Image Text:
y = 1 + 3x
> Find the area enclosed by the x-axis and the curve x =t3 + 1, y = 2t – t2.
> Find equations of the tangents to the curve x = 3t2 + 1, y = 2t3 + 1 that pass through the point (4, 3).
> At what point(s) on the curve x = 3t2 + 1, y = t3 - 1 does the tangent line have slope 1 2 ?
> Find the radius of convergence and interval of convergence of the series. E(-1)"nx" 'x' -1
> Graph the curve x = 22 cos t, y = sin t + sin 2t to discover where it crosses itself. Then find equations of both tangents at that point.
> Show that the curve x = cos t, y = sin t cos t has two tangents at (0, 0) and find their equations. Sketch the curve.
> Graph the curve in a viewing rectangle that displays all the important aspects of the curve. x= 14 + 41° – 81², y=21² – t
> Graph the curve in a viewing rectangle that displays all the important aspects of the curve. x = t* – 2t3 – 2t², y=t³ – t
> Use a graph to estimate the coordinates of the lowest point and the leftmost point on the curve x = t4 - 2t, y = t + t4. Then find the exact coordinates.
> Use a graph to estimate the coordinates of the rightmost point on the curve x = t - t6, y = et. Then use calculus to find the exact coordinates.
> Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work. *= e sino sinº, y = e cs0 cos0
> Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work. x = cos 0, y= cos 30
> Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work. x = t³ – 31, y =t} - 3t²
> (a) What is the radius of convergence of a power series? How do you find it? (b) What is the interval of convergence of a power series? How do you find it?
> Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work. х — — 31, у— ? - 3 x =
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? x = cos t, y = sin 2t, 0<t<
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? x = t - In t, y = t + In t
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? х — 1? + 1, у — е' — 1
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? x = e', y=te
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? х — + 1, у—r -1
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? x = t? + 1, y= t? + t
> Find an equation of the tangent to the curve at the given point. Then graph the curve and the tangent. := sin mt, y= t² + t; (0, 2)
> Find an equation of the tangent to the curve at the given point. Then graph the curve and the tangent. x = t? – 1, y=t² + t + 1; (0, 3)
> Find an equation of the tangent to the curve at the given point by two methods: (a) without eliminating the parameter and (b) by first eliminating the parameter. x = 1 + Vi, y= e"; (2, e)
> What is a power series?
> Find an equation of the tangent to the curve at the given point by two methods: (a) without eliminating the parameter and (b) by first eliminating the parameter. x = 1 + In t, y = t² + 2; (1, 3)
> Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. х — е' sin mt, у — е"; 1— 0 ,21. t =
> Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. x =t cos t, y=t sin t; t= T
> Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. x= Vĩ, Vi, y = t? – 2t; t=4
> Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. x = t³ + 1, y= 1ª + t; t= -1
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r = 2 + cos(90/4)
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= 1 + cos0 (Pac-Man curve)
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= | tan 0 |c* o| (valentine curve)
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= e sin o – 2 cos(40) (butterfly curve)
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= 1- 0.8 sin²0_ (hippopede) r =
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= 1 + 2 sin(0/2) (nephroid of Freeth)
> Find the points on the given curve where the tangent line is horizontal or vertical. r = e°
> Find the points on the given curve where the tangent line is horizontal or vertical. r=1+ cos 0
> Find the points on the given curve where the tangent line is horizontal or vertical. r=1- sin 0
> Find the points on the given curve where the tangent line is horizontal or vertical. -r= 3 cos 0
> Determine whether the series is absolutely convergent or conditionally convergent. (-1)* -1 In
> Match the polar equations with the graphs labeled I–VI. Give reasons for your choices. (Don’t use a graphing device.) (a) r= In 0, 1 < 0 < 6 (c) r= cos 30 (e) r= cos(0/2) (b) r= 0°, 0< 0 < 87 (d) r=2 + cos 30 (f)
> Sketch the curve (x2 + y2)3 = 4x2y2
> Test the series for convergence or divergence. E (v2 – 1)
> For each of the described curves, decide if the curve would be more easily given by a polar equation or a Cartesian equation. Then write an equation for the curve. (a) A circle with radius 5 and center (2, 3) (b) A circle centered at the origin with radi
> Find a polar equation for the curve represented by the given Cartesian equation. x? + y? = 2cx CX
> Find a polar equation for the curve represented by the given Cartesian equation. 4y2
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. (-1)* arctan n Σ n2
> Use a computer algebra system to find the Taylor polynomials Tn centered at a for n = 2, 3, 4, 5. Then graph these polynomials and f on the same screen. f(x) = V1 + x², a=0 %3D
> Identify the curve by finding a Cartesian equation for the curve. r= 5 cos 0
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r > 1, T< 0 < 2
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. 2 <r< 3, 57/3 < 0 < 7m/3
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. 1<r<3, п/6 <0 < 5п/6
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r> 0, T/4 < 0 < 37/4
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. () < r < 2, T<0 < 37/2
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r> 1
> Test the series for convergence or divergence. 1 (In n)n -2
> Plot the point whose polar coordinates are given. Then find the Cartesian coordinates of the point. (а) (4,4п/3) (b) (-2, Зп/4) (е) (-3, — п/3)
> Plot the point whose polar coordinates are given. Then find the Cartesian coordinates of the point. (а) (2, 3п/2) () (/2, т/4) (c) (-1, — п/6)
> Plot the point whose polar coordinates are given. Then find two other pairs of polar coordinates of this point, one with r > 0 and one with r (a) (2, 5п/6) (b) (1, —2т/3) (е) (-1,5п/4)
> (a) Find a formula for the area of the surface generated by rotating the polar curve / / about the line / (b) Find the surface area generated by rotating the lemniscate r = f(0), a < 0 < b (where f' is
> Use a calculator to find the length of the curve correct to four decimal places. If necessary, graph the curve to determine the parameter interval. r = sin(0/4)
> Use a calculator to find the length of the curve correct to four decimal places. If necessary, graph the curve to determine the parameter interval. r= sin(6 sin 0)
> Use a calculator to find the length of the curve correct to four decimal places. If necessary, graph the curve to determine the parameter interval. One loop of the curve r = cos 20
> Test the series for convergence or divergence. 1 Σ 1+1/n
> Find the exact length of the curve. Use a graph to determine the parameter interval. r= cos'(0/2)
> Find the exact length of the curve. Use a graph to determine the parameter interval. r = cos (0/4)
> Find the exact length of the polar curve. r= 2(1 + cos 0)
> Find the exact length of the polar curve. r= 0', 0< 0 < 27
> Find the exact length of the polar curve. r= 5°, 0 < 0 < 27
> Find the exact length of the polar curve. r = 2 cos 0, 0 < 0 <
> Test the series for convergence or divergence. 1 Σ n-1 n +n cos'n
> Find the area between a large loop and the enclosed small loop of the curve /
> Find the area inside the larger loop and outside the smaller loop of the limaçon /
> Find the area of the region that lies inside both curves. r = a sin 0, r = b cos 0, a > 0, b > 0
> Find the area of the region that lies inside both curves. r2 - 2 sin 20, r=1
> Find the area of the region that lies inside both curves. r = 3 + 2 cos 0, r= 3 + 2 sin0
> Find the area of the region that lies inside both curves. r = sin 20, r= cos 20
> Test the series for convergence or divergence. n Σ n +
> Find the area of the region that lies inside both curves. r= 1 + cos 0, r=1- cos 0
> Find the area of the region that lies inside both curves. r= 3 sin 0, r= 3 cos
> Find the area of the region that lies inside the first curve and outside the second curve. r = 3 sin 0, r= 2 – sin0
> Find the area of the region that lies inside the first curve and outside the second curve. r= 3 cos 0, r=1+ cos 0
> Find the area of the region that lies inside the first curve and outside the second curve. r = 1 + cos 0, r=2 – cos 0
> Find the area of the region that lies inside the first curve and outside the second curve. r? = 8 cos 20, r=2 %3D
> Find the area of the region that lies inside the first curve and outside the second curve. r = 1 - sin0, r= 1
> Find the area of the region that lies inside the first curve and outside the second curve. r = 4 sin 0, r= 2
> Test the series for convergence or divergence. (n!)" Σ 4n n-1
> Graph the curve and find the area that it encloses. r = 2 + sin 40
> Test the series for convergence or divergence. 5* Σ 3* + 4* k-1
> Find the area of the shaded region. r= /In 0, 1< 0<27
> Find the area of the shaded region. r = 4 + 3 sin 0
> Find the area of the shaded region. r=2 + cos 0
> Find the area of the shaded region. r? = sin 20
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r = 1/0, 7/2 <0 < 2m
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r = sin 0 + cos 0, 0 < 0 < T
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r= cos 0, 0 <0 </6
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r = e 0/4, T/2 < 0 <
> Test the series for convergence or divergence. E(-1)' j+ 5 j-1
> (a) Calculate the surface area of the ellipsoid that is generated by rotating an ellipse about its major axis. (b) What is the surface area if the ellipse is rotated about its minor axis?

