Question: Find the points on the curve where
Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work.
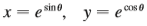
Transcribed Image Text:
*= e sino sinº, y = e cs0 cos0
> Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases. x = e + t, y= e' – t, -2 <t< 2
> Test the series for convergence or divergence. E (-1)*-1 4" n-
> Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases. x = t³ + t, _y= t² + 2, -2<t< 2
> Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases. x= 1 - t, y= 2t – t°, -1 <t<2
> A cow is tied to a silo with radius r by a rope just long enough to reach the opposite side of the silo. Find the grazing area available for the cow.
> (a) Show that the curvature at each point of a straight line is / = 0. (b) Show that the curvature at each point of a circle of radius r is / = 1/r.
> Use Formula 1 to derive Formula 6 from Formula 8.2.5 for the case in which the curve can be represented in the form /
> Find the radius of convergence and interval of convergence of the series. o n! -0
> Find the surface area generated by rotating the given curve about the y-axis. x = e' – t, y= 4e?, 0<t<1 = 4e2, 0<t<1
> Find the surface area generated by rotating the given curve about the y-axis. x = 3t, y = 2t², 0<t<5
> Find the exact area of the surface obtained by rotating the given curve about the x-axis. х —а сos'0, у —asin'0, 0<0< п/2
> Find the exact area of the surface obtained by rotating the given curve about the x-axis. x = 212 + 1/1, y= 8/t, 1<t< 3
> Find the exact area of the surface obtained by rotating the given curve about the x-axis. x = t, y = t, 0<t<1
> Set up an integral that represents the area of the surface obtained by rotating the given curve about the x-axis. Then use your calculator to find the surface area correct to four decimal places. x = t² – t, y=t+ t*, 0<t<1
> Set up an integral that represents the area of the surface obtained by rotating the given curve about the x-axis. Then use your calculator to find the surface area correct to four decimal places. x=t+ e', y= e ', 0<t< 1
> Set up an integral that represents the area of the surface obtained by rotating the given curve about the x-axis. Then use your calculator to find the surface area correct to four decimal places. x = sin t, y = sin 2t, 0<t< T/2
> Find the radius of convergence and interval of convergence of the series. (-1)"x" Σ n2
> Set up an integral that represents the area of the surface obtained by rotating the given curve about the x-axis. Then use your calculator to find the surface area correct to four decimal places. x = t sin t, y =t cos 1, 0<1<T/2
> A curve called Cornu’s spiral is defined by the parametric equations where C and S are the Fresnel functions that were introduced in Chapter 5. (a) Graph this curve. What happens as / and as / (b) Find the length of Cornuâ€&#
> (a) Graph the epitrochoid with equations What parameter interval gives the complete curve? (b) Use your CAS to find the approximate length of this curve. x= 11 cos t – 4 cos(11t/2) y = 11 sin t – 4 sin(11t/2)
> Find the distance traveled by a particle with position (x, y) as t varies in the given time interval. Compare with the length of the curve. x = cos't, y = cos t, 0 I< 4T
> Find the distance traveled by a particle with position (x, y) as t varies in the given time interval. Compare with the length of the curve. x = sin?t, y = cos?t, 0<t<3T
> Use Simpson’s Rule with n = 6 to estimate the length of the curve x = t – e', y = t + e', -6 <t< 6.
> Find the length of the loop of the curve x = 3t - t3 , y = 3t2.
> Find the radius of convergence and interval of convergence of the series. x" Σ 2n – 1
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Graph the curve x = sin t + sin +1.5t, y = cos t and find its length correct to four decimal places.
> Graph the curve and find its exact length. x = cos t + In(tan t), y= sin t, T/4 <t< 3/4
> Graph the curve and find its exact length. x = e' cos t, y = e' sin t, 0 <t<
> Find the exact length of the curve. х — 3 3 cos t - cos Зі, cos 31, y = 3 sin t – sin 3t, 0 <t<+
> Find the exact length of the curve. x = t sin t, y =t cos 1, 0 <1<1
> Find the exact length of the curve. x = e' – t, y = 4e"?, 0<t<2
> Find the exact length of the curve. x = 1 + 3t², y= 4 + 2t³, 0 <<t<1
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x = t + vt, y=t- Vi, 0<t<1
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x = t – 2 sin t, y=1-2 cos t, 0<t<4m
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x = t? – t, y= t“, 1<t<4
> Find the radius of convergence and interval of convergence of the series. (-1)"x" Σ 'n
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x = t + e¯', y=t – e', 0<t< 2
> Let R be the region enclosed by the loop of the curve in Example 1. (a) Find the area of R. (b) If 5 is rotated about the x-axis, find the volume of the resulting solid. (c) Find the centroid of R.
> Find the area enclosed by the x-axis and the curve x =t3 + 1, y = 2t – t2.
> Find equations of the tangents to the curve x = 3t2 + 1, y = 2t3 + 1 that pass through the point (4, 3).
> At what point(s) on the curve x = 3t2 + 1, y = t3 - 1 does the tangent line have slope 1 2 ?
> Find the radius of convergence and interval of convergence of the series. E(-1)"nx" 'x' -1
> Graph the curve x = 22 cos t, y = sin t + sin 2t to discover where it crosses itself. Then find equations of both tangents at that point.
> Show that the curve x = cos t, y = sin t cos t has two tangents at (0, 0) and find their equations. Sketch the curve.
> Graph the curve in a viewing rectangle that displays all the important aspects of the curve. x= 14 + 41° – 81², y=21² – t
> Graph the curve in a viewing rectangle that displays all the important aspects of the curve. x = t* – 2t3 – 2t², y=t³ – t
> Use a graph to estimate the coordinates of the lowest point and the leftmost point on the curve x = t4 - 2t, y = t + t4. Then find the exact coordinates.
> Use a graph to estimate the coordinates of the rightmost point on the curve x = t - t6, y = et. Then use calculus to find the exact coordinates.
> Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work. x = cos 0, y= cos 30
> Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work. x = t³ – 31, y =t} - 3t²
> (a) What is the radius of convergence of a power series? How do you find it? (b) What is the interval of convergence of a power series? How do you find it?
> Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work. х — — 31, у— ? - 3 x =
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? x = cos t, y = sin 2t, 0<t<
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? x = t - In t, y = t + In t
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? х — 1? + 1, у — е' — 1
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? x = e', y=te
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? х — + 1, у—r -1
> Find dy/dx and d2y/dx2. For which values of t is the curve concave upward? x = t? + 1, y= t? + t
> Find an equation of the tangent to the curve at the given point. Then graph the curve and the tangent. := sin mt, y= t² + t; (0, 2)
> Find an equation of the tangent to the curve at the given point. Then graph the curve and the tangent. x = t? – 1, y=t² + t + 1; (0, 3)
> Find an equation of the tangent to the curve at the given point by two methods: (a) without eliminating the parameter and (b) by first eliminating the parameter. x = 1 + Vi, y= e"; (2, e)
> What is a power series?
> Find an equation of the tangent to the curve at the given point by two methods: (a) without eliminating the parameter and (b) by first eliminating the parameter. x = 1 + In t, y = t² + 2; (1, 3)
> Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. х — е' sin mt, у — е"; 1— 0 ,21. t =
> Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. x =t cos t, y=t sin t; t= T
> Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. x= Vĩ, Vi, y = t? – 2t; t=4
> Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. x = t³ + 1, y= 1ª + t; t= -1
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r = 2 + cos(90/4)
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= 1 + cos0 (Pac-Man curve)
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= | tan 0 |c* o| (valentine curve)
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= e sin o – 2 cos(40) (butterfly curve)
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= 1- 0.8 sin²0_ (hippopede) r =
> Use a graphing device to graph the polar curve. Choose the parameter interval to make sure that you produce the entire curve. r= 1 + 2 sin(0/2) (nephroid of Freeth)
> Find the points on the given curve where the tangent line is horizontal or vertical. r = e°
> Find the points on the given curve where the tangent line is horizontal or vertical. r=1+ cos 0
> Find the points on the given curve where the tangent line is horizontal or vertical. r=1- sin 0
> Find the points on the given curve where the tangent line is horizontal or vertical. -r= 3 cos 0
> Determine whether the series is absolutely convergent or conditionally convergent. (-1)* -1 In
> Match the polar equations with the graphs labeled I–VI. Give reasons for your choices. (Don’t use a graphing device.) (a) r= In 0, 1 < 0 < 6 (c) r= cos 30 (e) r= cos(0/2) (b) r= 0°, 0< 0 < 87 (d) r=2 + cos 30 (f)
> Sketch the curve (x2 + y2)3 = 4x2y2
> Test the series for convergence or divergence. E (v2 – 1)
> For each of the described curves, decide if the curve would be more easily given by a polar equation or a Cartesian equation. Then write an equation for the curve. (a) A circle with radius 5 and center (2, 3) (b) A circle centered at the origin with radi
> Find a polar equation for the curve represented by the given Cartesian equation. x? + y? = 2cx CX
> Find a polar equation for the curve represented by the given Cartesian equation. 4y2
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. (-1)* arctan n Σ n2
> Use a computer algebra system to find the Taylor polynomials Tn centered at a for n = 2, 3, 4, 5. Then graph these polynomials and f on the same screen. f(x) = V1 + x², a=0 %3D
> Find a polar equation for the curve represented by the given Cartesian equation. y = 1 + 3x
> Identify the curve by finding a Cartesian equation for the curve. r= 5 cos 0
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r > 1, T< 0 < 2
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. 2 <r< 3, 57/3 < 0 < 7m/3
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. 1<r<3, п/6 <0 < 5п/6
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r> 0, T/4 < 0 < 37/4
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. () < r < 2, T<0 < 37/2
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r> 1
> Test the series for convergence or divergence. 1 (In n)n -2
> Plot the point whose polar coordinates are given. Then find the Cartesian coordinates of the point. (а) (4,4п/3) (b) (-2, Зп/4) (е) (-3, — п/3)
> Plot the point whose polar coordinates are given. Then find the Cartesian coordinates of the point. (а) (2, 3п/2) () (/2, т/4) (c) (-1, — п/6)
> Plot the point whose polar coordinates are given. Then find two other pairs of polar coordinates of this point, one with r > 0 and one with r (a) (2, 5п/6) (b) (1, —2т/3) (е) (-1,5п/4)
> (a) Find a formula for the area of the surface generated by rotating the polar curve / / about the line / (b) Find the surface area generated by rotating the lemniscate r = f(0), a < 0 < b (where f' is

