Question: Find the area of the region that
Find the area of the region that lies inside both curves.
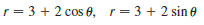
Transcribed Image Text:
r = 3 + 2 cos e, r= 3 + 2 sin e
> If sin x = 1/3 and sec y = 5/4, where x and y lie between 0 and π/2, evaluate the expression. sin (x + y)
> Prove the identity. cos 3θ = 4 cos3θ - 3 cos θ
> Prove the identity. tan 2θ = 2 tan θ/ 1 – tan2θ
> Use Definition 4 to prove that limn→∞ n3 = ∞.
> Use Definition 3 to prove that if lim n→∞ |an| = 0, then limn→∞ an = 0.
> If a ball is thrown upward from the top of a building 128 ft high with an initial velocity of 16 ft/s, then the height above the ground seconds later will be h = 128 + 16t – 16t2 During what time interval will the ball be at least 32 ft above the ground?
> Use Definition 3 to prove that limn→∞ r n = 0 when |r| < 1.
> Prove the identity. sin (π/2 + x) = cos x
> Prove each equation. (a). Equation 14a (b). Equation 14b
> Convert from degrees to radians. (a). 3150 (b). 360
> (a). Determine how large we have to take x so that 1/x < 0.0001 (b). Use Definition 2 to prove that limx→∞ 1/x2 = 0.
> Find, correct to five decimal places, the length of the side labeled x. 22 сm х 8
> Find, correct to five decimal places, the length of the side labeled x. 8 cm
> Prove the statement using the ∈, δ definition of a limit and illustrate with a diagram like Figure 7. Figure 7: y A /y= 4x – 5 7+e 7 1-E 3-6 3+8 lim (tx + 3) = 2 エ→-2
> Prove the statement using the ∈, δ definition of a limit and illustrate with a diagram like Figure 7. Figure 7: y A /y= 4x – 5 7+e 7 1-E 3-6 3+8 lim (1 – 4x) = 13 I-3
> Given that limx→2 (5x – 7) = 3, illustrate Definition 1 by finding values of δ that correspond to ∈ = 0.1, ∈ = 0.05, and ∈ = 0.01.
> As dry air moves upward, it expands and in so doing cools at a rate of about C for each 100-m rise, up to about 12 km. (a). If the ground temperature is 200C, write a formula for the temperature at height h. (b). What range of temperature can be expected
> Use the given graph of f to find a number such that if 0 < |x - 5|< 8 \f(x) – 3|< 0.6 then y. 3.6 3 2.4 5 5 5.7 4.
> (a). Find a number δ such that if |x – 2| < δ, then |4x – 8| < ∈, where ∈ = 0.1. (b). Repeat part (a) with ∈ = 0.01.
> Find the exact trigonometric ratios for the angle whose radian measure is given. 4π/3
> Find the exact trigonometric ratios for the angle whose radian measure is given. 3π/4
> Draw, in standard position, the angle whose measure is given. (a) rad 3 (b) —3 гad
> Use the given graph of f (x) = 1/x to find a number δ such that if |x - 2| < 8 then 0.5 < 0.2 y. 1+ 0.7 0.5 0.3 10 10 3 2.
> Draw, in standard position, the angle whose measure is given. 37 rad 4 (а) 315° (b)
> If a circle has radius 10 cm, find the length of the arc subtended by a central angle of 720.
> Find the length of a circular arc subtended by an angle of π/12 rad if the radius of the circle is 36 cm.
> Prove the identity. (sin x + cos x)2 = 1 + sin 2x
> Prove the identity. sin θ cot θ = cos θ
> Prove the identity. sin (π - x) = sin x
> Prove each equation. (a). Equation 10a (b). Equation 10b
> Find, correct to five decimal places, the length of the side labeled x. 40° 25 cm
> Find, correct to five decimal places, the length of the side labeled x. 10 cm 35°
> Find the remaining trigonometric ratios. tan a = 2, 0 < α < π/2
> Find the remaining trigonometric ratios. Sin θ = 3/5, 0 < θ < π/2
> Convert from degrees to radians. (a). 2100 (b). 90
> Sketch the graph of the equation. xy = 0
> Sketch the graph of the equation. y = -2
> Sketch the graph of the equation. x = 3
> Find the area inside the larger loop and outside the smaller loop of the limaçon r = 1/2 + cos θ.
> (a). Show that the points A (-1, 3), B (3, 11), and C (5, 15) are collinear (lie on the same line) by showing that |AB| + |BC| = |AC|. (b). Use slopes to show that A, B, and C are collinear.
> Show that the points (-2, 9), (4, 6), (1, 0), and (-5, 3) are the vertices of a square.
> Find an equation of the perpendicular bisector of the line segment joining the points A (1, 4) and B (7, -2).
> Find the midpoint of the line segment joining the points (1, 3) and (7, 15).
> Show that the midpoint of the line segment from P1 (x1, y1) to P2 (x2, y2) is (x1 + x2/2, y1 + y2/2).
> Show that the lines 3x – 5y + 19 = 0 and 10x + 6y – 50 = 0 are perpendicular and find their point of intersection.
> Show that the lines 2x – y = 4 and 6x – 2y = 10 are not parallel and find their point of intersection.
> Show that the equation represents a circle and find the center and radius. x² + y² + 6y + 2 = 0
> Find the slope of the line through P and Q. P (-1, -4), Q (6, 0)
> Show that the equation represents a circle and find the center and radius. x? + y? – 4x + 10y + 13 = 0
> Find an equation of a circle that satisfies the given conditions. Center (-1, 5), passes through (-4, -6)
> Find an equation of a circle that satisfies the given conditions. Center (3, -1), radius 5
> Sketch the region in the xy-plane. {(x, y) | -x < y < 1/2 (x + 3)}
> Sketch the region in the xy-plane. {(x, y) |1 + x < y < 1 – 2x}
> Sketch the region in the xy-plane. {(x, y) | y > 2x – 1}
> Sketch the region in the xy-plane. {(x, y) |0 < y < 4 and x < 2}
> Sketch the region in the xy-plane. {(x. y) ||x| < 3 and |y| < 2}
> Sketch the region in the xy-plane. {(x, y) ||x| < 2
> Sketch the region in the xy-plane. {(x, y) | x > 1 and y < 3}
> Find the slope of the line through P and Q. P (-3, 3), Q (-1, -6)
> (a). Use a graph to guess the value of the limit (b). Use a graph of the sequence in part (a) to find the smallest values of N that correspond to ∈ = 0.1 and ∈ = 0.001 in Definition 3. lim - n!
> Sketch the region in the xy-plane. {(x, y) |x < 0}
> Find the slope and -intercept of the line and draw its graph. 4x + 5y = 10
> Find the slope and -intercept of the line and draw its graph. 3x – 4y = 12
> Find the slope and -intercept of the line and draw its graph. 2x – 3y + 6 = 0
> Find the slope and -intercept of the line and draw its graph. x + 3y = 0
> Find an equation of the line that satisfies the given conditions. Through (1/2, -2/3), perpendicular to the line 4x – 8y = 1
> Find an equation of the line that satisfies the given conditions. Through (-1, -2), perpendicular to the line 2x + 5y + 8 = 0
> Find an equation of the line that satisfies the given conditions. y-intercept 6, parallel to the line 2x + 3y + 4 = 0
> Find an equation of the line that satisfies the given conditions. Through (1, -6), parallel to the line x + 2y = 6
> Find an equation of the line that satisfies the given conditions. Through (4, 5), parallel to the -axis
> (a). For what values of x is it true that 1/x2 > 1,000,000 (b). The precise definition of limx→a f (x) = ∞ states that for every positive number M (no matter how large) there is a corresponding positive number δ such that if 0 < |x – a| < δ, then f (x) >
> Find the distance between the points. (1, -3) (5, 7)
> Find an equation of the line that satisfies the given conditions. Through (4, 5), parallel to the -axis
> Find an equation of the line that satisfies the given conditions. x-intercept -8, y-intercept 6
> Find an equation of the line that satisfies the given conditions. x-intercept, y-intercept -3
> Find an equation of the line that satisfies the given conditions. Slope 2/5, y-intercept 4
> Find an equation of the line that satisfies the given conditions. slope 3, y-intercept -2
> Find an equation of the line that satisfies the given conditions. Through (-1, -2), and (4, 4)
> Find an equation of the line that satisfies the given conditions. Through (2, 1), and (1, 6)
> Find an equation of the line that satisfies the given conditions. Through (-3, -5), slope -7/2
> Find an equation of the line that satisfies the given conditions. Through (2, -3), slope 6
> For the limit illustrate Definition 2 by finding values of N that correspond to ∈ = 0.5 and ∈ = 0.1. 4x2 + 1 lim = 2 x + 1
> Sketch the graph of the equation. |y| = 1
> Find the distance between the points. (1, 1), (4, 5)
> Rewrite the expression without using the absolute value symbol. |x2 + 1|
> Rewrite the expression without using the absolute value symbol. |2x – 1|
> Rewrite the expression without using the absolute value symbol. |x + 1|
> Rewrite the expression without using the absolute value symbol. |x – 2| if x > 2
> Rewrite the expression without using the absolute value symbol. |x – 2| if x < 2
> Show that if 0 < a < b, then a2 < b2.
> Prove that |ab| = |a||b|. [Hint: Use Equation 3.]
> Solve the inequality ax + b + c for x, assuming that a, b, and are negative constants.
> Use a graph to find a number N such that if x > N then |6х? + 5х — 3 3 < 0.2 2x2 – 1
> Solve the inequality a (bx – c) > bc for x, assuming that a, b, and are positive constants.
> Solve the inequality. |5x – 2| < 6
> Rewrite the expression without using the absolute value symbol. ||-2| - |-3||
> Solve the inequality. |2x – 3| < 0.4
> Solve the inequality. |x + 1|> 3
> Solve the inequality. |x + 5| > 2
> Solve the inequality. |x – 6| < 0.1

