Question: Prove the statement using the ∈, δ definition of
Prove the statement using the ∈, δ definition of a limit and illustrate with a diagram like Figure 7.
Figure 7:
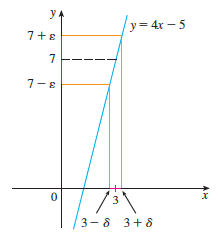
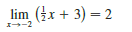
Transcribed Image Text:
y A /y= 4x – 5 7+e 7 1-E 3-6 3+8 lim (tx + 3) = 2 エ→-2
> Write the sum in sigma notation. 1+ 2 + 3 + 4 + … + 10
> Write the sum in expanded form. ∑nj=1 f (xi) ∆xi
> Write the sum in expanded form. ∑5i=1 √i
> Use Definition 1 to prove that limx→0 x3 = 0
> Find the radius of a circular sector with angle 3π/4 and arc length 6 cm.
> A circle has radius 1.5 m. What angle is subtended at the center of the circle by an arc 1 m long?
> Use a graph to find a number δ such that if 2x |x - 1|< 8 then - 0.4 <0.1 x? + 4
> Find the foci of the ellipse x2 + 4y2 = 4 and sketch its graph.
> (a). Use a computer algebra system to find the partial fraction decomposition of the function (b). Use part (a) to find ff (x) dx (by hand) and compare with the result of using the CAS to integrate f directly. Comment on any discrepancy. 4x3 — 27х?
> Use a graph to find a number δ such that if < 8 4 | tan x – 1| < 0.2 then
> Rewrite the expression without using the absolute value symbol. |1 - 2x2|
> Find the focus and directrix of the parabola y = x2. Illustrate with a diagram.
> Rewrite the expression without using the absolute value symbol. |5 – 23|
> (a). Show that if the - and -intercepts of a line are nonzero numbers a and b, then the equation of the line can be put in the form x/a + y/b = 1 This equation is called the two-intercept form of an equation of a line. (b). Use part (a) to find an equati
> Use the addition formula for cosine and the identities to prove the subtraction formula (13a) for the sine function. (÷-)- : )-i : )- sin 2 cos sin e cos e
> Use the formula in Exercise 43 to prove the addition formula for cosine (12b). Exercise 43: Use the figure to prove the subtraction formula cos (α – β) = cos α cos β + sin Î&pl
> Use the figure to prove the subtraction formula cos (α – β) = cos α cos β + sin α sin β [Hint: Compute c2 in two ways (using the Law of Cosines from Exercise
> In order to find the distance |AB| across a small inlet, a point C was located as in the figure and the following measurements were recorded: Use the Law of Cosines from Exercise 41 to find the required distance. LC = 103° |AC|= 820 m | BC| = 910
> Prove the Law of Cosines: If a triangle has sides with lengths a, b, and c, and θ is the angle between the sides with lengths a and b, then [Hint: Introduce a coordinate system so that θ is in standard position, as in the fig
> The points of intersection of the cardioid r = 1 + sin θ and the spiral loop r = 2θ, -π/2 < θ < π/2, can’t be found exactly. Use a graphing device to find the approximate values of θ at which they intersect. Then use these values to estimate the area th
> Graph the function by starting with the graphs in Figures 13 and 14 and applying the transformations of Section 1.3 where appropriate. Figures 13: y = |sin x| 1 37 -1 (a) f(x) = sin x (b) g(x) 3 сos х + 1. kle +
> Convert from radians to degrees. (a). -7π/2 (b). 8π/4
> Graph the function by starting with the graphs in Figures 13 and 14 and applying the transformations of Section 1.3 where appropriate. Figures 13: 1 37 -1 (a) f(x) = sin x (b) g(x) 3 сos х + 1. kle + 1 y = 3 y=z tan(x 2
> Graph the function by starting with the graphs in Figures 13 and 14 and applying the transformations of Section 1.3 where appropriate. Figures 13: y = tan 2x 1 37 -1 (a) f(x) = sin x (b) g(x) 3 сos х + 1. kle +
> Graph the function by starting with the graphs in Figures 13 and 14 and applying the transformations of Section 1.3 where appropriate. Figures 13: 1 37 -1 (a) f(x) = sin x (b) g(x) 3 сos х + 1. kle + TT y = cos x 3
> Find all values of x in the interval [0, 2π] that satisfy the inequality. sin x > cos x
> Find all values of x in the interval [0, 2π] that satisfy the inequality. -1 < tan x < 1
> Find all values of x in the interval [0, 2π] that satisfy the inequality. 2 cos x + 1 > 0
> Find all values of x in the interval [0, 2π] that satisfy the inequality. sin x < 1/2
> Find all values of x in the interval [0, 2Ï€] that satisfy the equation. |tan x| = 1
> Solve the inequality in terms of intervals and illustrate the solution set on the real number line. -3 <<1
> Find all values of x in the interval [0, 2Ï€] that satisfy the equation. sin 2x = cos x
> Find all values of x in the interval [0, 2Ï€] that satisfy the equation. 2 sin'x = 1
> Convert from radians to degrees. (a). 4π (b). -3π/4
> Find all values of x in the interval [0, 2Ï€] that satisfy the equation. 2 cos x - 1 = 0
> If sin x = 1/3 and sec y = 5/4, where x and y lie between 0 and π/2, evaluate the expression. cos 2y
> If sin x = 1/3 and sec y = 5/4, where x and y lie between 0 and π/2, evaluate the expression. sin (x + y)
> Prove the identity. cos 3θ = 4 cos3θ - 3 cos θ
> Prove the identity. tan 2θ = 2 tan θ/ 1 – tan2θ
> Use Definition 4 to prove that limn→∞ n3 = ∞.
> Use Definition 3 to prove that if lim n→∞ |an| = 0, then limn→∞ an = 0.
> If a ball is thrown upward from the top of a building 128 ft high with an initial velocity of 16 ft/s, then the height above the ground seconds later will be h = 128 + 16t – 16t2 During what time interval will the ball be at least 32 ft above the ground?
> Use Definition 3 to prove that limn→∞ r n = 0 when |r| < 1.
> Prove the identity. sin (π/2 + x) = cos x
> Prove each equation. (a). Equation 14a (b). Equation 14b
> Convert from degrees to radians. (a). 3150 (b). 360
> (a). Determine how large we have to take x so that 1/x < 0.0001 (b). Use Definition 2 to prove that limx→∞ 1/x2 = 0.
> Find, correct to five decimal places, the length of the side labeled x. 22 сm х 8
> Find, correct to five decimal places, the length of the side labeled x. 8 cm
> Prove the statement using the ∈, δ definition of a limit and illustrate with a diagram like Figure 7. Figure 7: y A /y= 4x – 5 7+e 7 1-E 3-6 3+8 lim (1 – 4x) = 13 I-3
> Given that limx→2 (5x – 7) = 3, illustrate Definition 1 by finding values of δ that correspond to ∈ = 0.1, ∈ = 0.05, and ∈ = 0.01.
> As dry air moves upward, it expands and in so doing cools at a rate of about C for each 100-m rise, up to about 12 km. (a). If the ground temperature is 200C, write a formula for the temperature at height h. (b). What range of temperature can be expected
> Use the given graph of f to find a number such that if 0 < |x - 5|< 8 \f(x) – 3|< 0.6 then y. 3.6 3 2.4 5 5 5.7 4.
> (a). Find a number δ such that if |x – 2| < δ, then |4x – 8| < ∈, where ∈ = 0.1. (b). Repeat part (a) with ∈ = 0.01.
> Find the exact trigonometric ratios for the angle whose radian measure is given. 4π/3
> Find the exact trigonometric ratios for the angle whose radian measure is given. 3π/4
> Draw, in standard position, the angle whose measure is given. (a) rad 3 (b) —3 гad
> Use the given graph of f (x) = 1/x to find a number δ such that if |x - 2| < 8 then 0.5 < 0.2 y. 1+ 0.7 0.5 0.3 10 10 3 2.
> Draw, in standard position, the angle whose measure is given. 37 rad 4 (а) 315° (b)
> If a circle has radius 10 cm, find the length of the arc subtended by a central angle of 720.
> Find the length of a circular arc subtended by an angle of π/12 rad if the radius of the circle is 36 cm.
> Prove the identity. (sin x + cos x)2 = 1 + sin 2x
> Prove the identity. sin θ cot θ = cos θ
> Prove the identity. sin (π - x) = sin x
> Prove each equation. (a). Equation 10a (b). Equation 10b
> Find, correct to five decimal places, the length of the side labeled x. 40° 25 cm
> Find, correct to five decimal places, the length of the side labeled x. 10 cm 35°
> Find the remaining trigonometric ratios. tan a = 2, 0 < α < π/2
> Find the remaining trigonometric ratios. Sin θ = 3/5, 0 < θ < π/2
> Convert from degrees to radians. (a). 2100 (b). 90
> Sketch the graph of the equation. xy = 0
> Sketch the graph of the equation. y = -2
> Sketch the graph of the equation. x = 3
> Find the area inside the larger loop and outside the smaller loop of the limaçon r = 1/2 + cos θ.
> (a). Show that the points A (-1, 3), B (3, 11), and C (5, 15) are collinear (lie on the same line) by showing that |AB| + |BC| = |AC|. (b). Use slopes to show that A, B, and C are collinear.
> Show that the points (-2, 9), (4, 6), (1, 0), and (-5, 3) are the vertices of a square.
> Find an equation of the perpendicular bisector of the line segment joining the points A (1, 4) and B (7, -2).
> Find the midpoint of the line segment joining the points (1, 3) and (7, 15).
> Show that the midpoint of the line segment from P1 (x1, y1) to P2 (x2, y2) is (x1 + x2/2, y1 + y2/2).
> Show that the lines 3x – 5y + 19 = 0 and 10x + 6y – 50 = 0 are perpendicular and find their point of intersection.
> Show that the lines 2x – y = 4 and 6x – 2y = 10 are not parallel and find their point of intersection.
> Show that the equation represents a circle and find the center and radius. x² + y² + 6y + 2 = 0
> Find the slope of the line through P and Q. P (-1, -4), Q (6, 0)
> Show that the equation represents a circle and find the center and radius. x? + y? – 4x + 10y + 13 = 0
> Find the area of the region that lies inside both curves. r = 3 + 2 cos e, r= 3 + 2 sin e
> Find an equation of a circle that satisfies the given conditions. Center (-1, 5), passes through (-4, -6)
> Find an equation of a circle that satisfies the given conditions. Center (3, -1), radius 5
> Sketch the region in the xy-plane. {(x, y) | -x < y < 1/2 (x + 3)}
> Sketch the region in the xy-plane. {(x, y) |1 + x < y < 1 – 2x}
> Sketch the region in the xy-plane. {(x, y) | y > 2x – 1}
> Sketch the region in the xy-plane. {(x, y) |0 < y < 4 and x < 2}
> Sketch the region in the xy-plane. {(x. y) ||x| < 3 and |y| < 2}
> Sketch the region in the xy-plane. {(x, y) ||x| < 2
> Sketch the region in the xy-plane. {(x, y) | x > 1 and y < 3}
> Find the slope of the line through P and Q. P (-3, 3), Q (-1, -6)
> (a). Use a graph to guess the value of the limit (b). Use a graph of the sequence in part (a) to find the smallest values of N that correspond to ∈ = 0.1 and ∈ = 0.001 in Definition 3. lim - n!
> Sketch the region in the xy-plane. {(x, y) |x < 0}
> Find the slope and -intercept of the line and draw its graph. 4x + 5y = 10
> Find the slope and -intercept of the line and draw its graph. 3x – 4y = 12
> Find the slope and -intercept of the line and draw its graph. 2x – 3y + 6 = 0

