[SOLVED] Find the constant a, or the constants

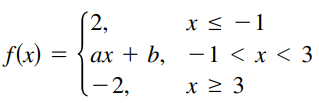
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. The limit of the greatest integer function as x approaches 0 from the left is −1.

> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. The Intermediate Value Theorem guarantees that f(a) and f(b) differ in sign when a continuous function f has at least one zero on [a,

> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If f(x) = g(x) for x ≠ c and f(c) ≠ g(c), then either f or g is not continuous at c.

> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.

> Describe the difference between a discontinuity that is removable and a discontinuity that is non-removable. Then give an example of a function that satisfies each description. a. A function with a non-removable discontinuity at x = 4 b. A function with

> If the functions f and g are continuous for all real x, is f + g always continuous for all real x? Is f / g always continuous for all real x? If either is not continuous, give an example to verify your conclusion.

> Sketch the graph of any function f such that Is the function continuous at x = 3? Explain.

> Write a function that is continuous on (a, b) but not continuous on [a, b].

> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. f(x) = x – x3 / x - 4, [1, 3], f(c) = 3

> Sketch the graph of fâ². Explain how you found your answer.

> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. f(x) = ∛x + 8, [-9, -6], f(c) = 6

> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. f(x) = √x + 7 – 2, [0, 5], f(c) = 1

> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. f(x) = x2 - 6x + 8, [0, 3], f(c) = 0

> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. f(x) = x2 + x − 1, [0, 5], f(c) = 11

> Use the Intermediate Value Theorem and a graphing utility to approximate the zero of the function in the interval [0, 1]. Repeatedly “zoom in” on the graph of the function to approximate the zero accurate to two decimal places. Use the zero or root featu

> Sketch the graph of fâ². Explain how you found your answer.

> Insert the proper inequality symbol () between the given quantities. Identify or sketch each of the quantities on the figure. a. / b. /

> Explain why the function has at least two zeros in the interval [1, 5]. f(x) = 2 cos x

> Explain why the function has at least two zeros in the interval [1, 5]. f(x) = (x - 3)2 – 2

> Explain why the function has at least one zero in the given interval. Function: f(x) = -(5 / x) + tan - πx / 10 Interval: [1, 4]

> Explain why the function has at least one zero in the given interval. Function: f(x) = x2 – 2 - cos x Interval: [0, π]

> Explain why the function has at least one zero in the given interval. Function: f(x) = x3 + 5x - 3 Interval: [0, 1]

> Explain why the function has at least one zero in the given interval. Function: f(x) = 1/12 x4 – x3 + 4 Interval: [1, 2]

> Describe the interval(s) on which the function is continuous.

> Describe the interval(s) on which the function is continuous. f(x) = cos 1 / x

> Describe the interval(s) on which the function is continuous. f(x) = sec πx / 4

> Sketch the graph of fâ². Explain how you found your answer.

> Describe the interval(s) on which the function is continuous. f(x) = x √x + 3

> Describe the interval(s) on which the function is continuous. f(x) = 3 - √x

> Describe the interval(s) on which the function is continuous. f(x) = x + 1 / √x

> Describe the interval(s) on which the function is continuous. f(x) = x / x2 + x + 2

> Use a graphing utility to graph the function. Use the graph to determine any x-values at which the function is not continuous.

> Use a graphing utility to graph the function. Use the graph to determine any x-values at which the function is not continuous. f(x) = [[x]] - x

> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = sin x g(x) = x2

> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = tan x g(x) = x / 2

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = 1 / √x - 1 Line: x + 2y + 7 = 0

> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = 1 / √x g(x) = x - 1

> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = 1 / x - 6 g(x) = x2 + 5

> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = 5x + 1 g(x) = x3

> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = x2 g(x) = x – 1

> Find the constant a, or the constants a and b, such that the function is continuous on the entire real number line.

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = 1 / √x Line: x + 2y - 6 = 0

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = tan πx / 2

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = csc 2x

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 2│x - 3│ / x - 3

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = │x + 7│ / x + 7

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = x3 + 2 Line: 3x - y - 4 = 0

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x + 2 / x2 – x - 6

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x + 2 / x2 – 3x - 10

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x / x2 – 4

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x / x2 – x

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = sin x – 8x

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 3x – cos x

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 1 / x2 + 1

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 1 / 4 – x2

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 4 / x - 6

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 6 / x

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = x3 Line: 3x - y + 1 = 0

> Discuss the continuity of the function on the closed interval. Function: g(x) = 1 / x2 - 4 Interval: [-1, 2]

> Discuss the continuity of the function on the closed interval. Function: / Interval: [-1, 4]

> Discuss the continuity of the function on the closed interval. Function: f(t) = 3 - √9 – t2 Interval: [-3, 3]

> Discuss the continuity of the function on the closed interval. Function: g(x) = √49 – x2 Interval: [-7, 7]

> Discuss the continuity of the function.

> Discuss the continuity of the function. f(x) = x2 - 1/x + 1

> Discuss the continuity of the function. f(x) = 1/x2 - 4

> Find the limit (if it exists). If it does not exist, explain why.

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = 2x2 Line: 4x + y + 3 = 0

> Find the limit (if it exists). If it does not exist, explain why.

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = -1/4 x2 Line: x + y = 0

> Find the limit (if it exists). If it does not exist, explain why.

Question: Find the constant a, or the constants