Question: Find the x-values (if any) at
Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
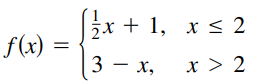
> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. f(x) = x2 + x − 1, [0, 5], f(c) = 11
> Use the Intermediate Value Theorem and a graphing utility to approximate the zero of the function in the interval [0, 1]. Repeatedly “zoom in” on the graph of the function to approximate the zero accurate to two decimal places. Use the zero or root featu
> Use the Intermediate Value Theorem and a graphing utility to approximate the zero of the function in the interval [0, 1]. Repeatedly “zoom in” on the graph of the function to approximate the zero accurate to two decimal places. Use the zero or root featu
> Use the Intermediate Value Theorem and a graphing utility to approximate the zero of the function in the interval [0, 1]. Repeatedly “zoom in” on the graph of the function to approximate the zero accurate to two decimal places. Use the zero or root featu
> Use the Intermediate Value Theorem and a graphing utility to approximate the zero of the function in the interval [0, 1]. Repeatedly “zoom in” on the graph of the function to approximate the zero accurate to two decimal places. Use the zero or root featu
> Use the Intermediate Value Theorem and a graphing utility to approximate the zero of the function in the interval [0, 1]. Repeatedly “zoom in” on the graph of the function to approximate the zero accurate to two decimal places. Use the zero or root featu
> Use the Intermediate Value Theorem and a graphing utility to approximate the zero of the function in the interval [0, 1]. Repeatedly “zoom in” on the graph of the function to approximate the zero accurate to two decimal places. Use the zero or root featu
> Sketch the graph of f′. Explain how you found your answer.
> Insert the proper inequality symbol () between the given quantities. Identify or sketch each of the quantities on the figure. a. / b. /
> Explain why the function has at least two zeros in the interval [1, 5]. f(x) = 2 cos x
> Explain why the function has at least two zeros in the interval [1, 5]. f(x) = (x - 3)2 – 2
> Explain why the function has at least one zero in the given interval. Function: f(x) = -(5 / x) + tan - πx / 10 Interval: [1, 4]
> Explain why the function has at least one zero in the given interval. Function: f(x) = x2 – 2 - cos x Interval: [0, π]
> Explain why the function has at least one zero in the given interval. Function: f(x) = x3 + 5x - 3 Interval: [0, 1]
> Explain why the function has at least one zero in the given interval. Function: f(x) = 1/12 x4 – x3 + 4 Interval: [1, 2]
> Describe the interval(s) on which the function is continuous.
> Describe the interval(s) on which the function is continuous.
> Describe the interval(s) on which the function is continuous. f(x) = cos 1 / x
> Describe the interval(s) on which the function is continuous. f(x) = sec πx / 4
> Sketch the graph of f′. Explain how you found your answer.
> Describe the interval(s) on which the function is continuous. f(x) = x √x + 3
> Describe the interval(s) on which the function is continuous. f(x) = 3 - √x
> Describe the interval(s) on which the function is continuous. f(x) = x + 1 / √x
> Describe the interval(s) on which the function is continuous. f(x) = x / x2 + x + 2
> Use a graphing utility to graph the function. Use the graph to determine any x-values at which the function is not continuous.
> Use a graphing utility to graph the function. Use the graph to determine any x-values at which the function is not continuous.
> Use a graphing utility to graph the function. Use the graph to determine any x-values at which the function is not continuous.
> Use a graphing utility to graph the function. Use the graph to determine any x-values at which the function is not continuous. f(x) = [[x]] - x
> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = sin x g(x) = x2
> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = tan x g(x) = x / 2
> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = 1 / √x - 1 Line: x + 2y + 7 = 0
> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = 1 / √x g(x) = x - 1
> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = 1 / x - 6 g(x) = x2 + 5
> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = 5x + 1 g(x) = x3
> Discuss the continuity of the composite function h(x) = f(g(x)). f(x) = x2 g(x) = x – 1
> Find the constant a, or the constants a and b, such that the function is continuous on the entire real number line.
> Find the constant a, or the constants a and b, such that the function is continuous on the entire real number line.
> Find the constant a, or the constants a and b, such that the function is continuous on the entire real number line.
> Find the constant a, or the constants a and b, such that the function is continuous on the entire real number line.
> Find the constant a, or the constants a and b, such that the function is continuous on the entire real number line.
> Find the constant a, or the constants a and b, such that the function is continuous on the entire real number line.
> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = 1 / √x Line: x + 2y - 6 = 0
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = tan πx / 2
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = csc 2x
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 2│x - 3│ / x - 3
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = │x + 7│ / x + 7
> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = x3 + 2 Line: 3x - y - 4 = 0
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x + 2 / x2 – x - 6
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x + 2 / x2 – 3x - 10
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x / x2 – 4
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x / x2 – x
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = sin x – 8x
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 3x – cos x
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 1 / x2 + 1
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 1 / 4 – x2
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 4 / x - 6
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 6 / x
> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = x3 Line: 3x - y + 1 = 0
> Discuss the continuity of the function on the closed interval. Function: g(x) = 1 / x2 - 4 Interval: [-1, 2]
> Discuss the continuity of the function on the closed interval. Function: / Interval: [-1, 4]
> Discuss the continuity of the function on the closed interval. Function: f(t) = 3 - √9 – t2 Interval: [-3, 3]
> Discuss the continuity of the function on the closed interval. Function: g(x) = √49 – x2 Interval: [-7, 7]
> Discuss the continuity of the function.
> Discuss the continuity of the function.
> Discuss the continuity of the function. f(x) = x2 - 1/x + 1
> Discuss the continuity of the function. f(x) = 1/x2 - 4
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = 2x2 Line: 4x + y + 3 = 0
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = -1/4 x2 Line: x + y = 0
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> find the limit (if it exists). If it does not exist, explain why.
> find the limit (if it exists). If it does not exist, explain why.
> find the limit (if it exists). If it does not exist, explain why.
> find the limit (if it exists). If it does not exist, explain why.
> Use the graph to determine each limit, and discuss the continuity of the function. a. / b. / c. /
> Use the graph to determine each limit, and discuss the continuity of the function. a. / b. / c. /
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x - 1
> Use the graph to determine each limit, and discuss the continuity of the function. a. / b. / c. /
> Use the graph to determine each limit, and discuss the continuity of the function. a. / b. / c. /
> Use the graph to determine each limit, and discuss the continuity of the function. a. / b. / c. /
> Use the graph to determine each limit, and discuss the continuity of the function. a. / b. / c. /

