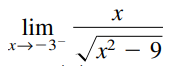[SOLVED] Find the limit (if it exists). If

> Find the constant a, or the constants a and b, such that the function is continuous on the entire real number line.

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = 1 / √x Line: x + 2y - 6 = 0

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = tan πx / 2

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = csc 2x

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 2│x - 3│ / x - 3

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = │x + 7│ / x + 7

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = x3 + 2 Line: 3x - y - 4 = 0

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x + 2 / x2 – x - 6

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x + 2 / x2 – 3x - 10

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x / x2 – 4

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = x / x2 – x

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = sin x – 8x

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 3x – cos x

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 1 / x2 + 1

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 1 / 4 – x2

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 4 / x - 6

> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable? f(x) = 6 / x

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = x3 Line: 3x - y + 1 = 0

> Discuss the continuity of the function on the closed interval. Function: g(x) = 1 / x2 - 4 Interval: [-1, 2]

> Discuss the continuity of the function on the closed interval. Function: / Interval: [-1, 4]

> Discuss the continuity of the function on the closed interval. Function: f(t) = 3 - √9 – t2 Interval: [-3, 3]

> Discuss the continuity of the function on the closed interval. Function: g(x) = √49 – x2 Interval: [-7, 7]

> Discuss the continuity of the function.

> Discuss the continuity of the function. f(x) = x2 - 1/x + 1

> Discuss the continuity of the function. f(x) = 1/x2 - 4

> Find the limit (if it exists). If it does not exist, explain why.

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = 2x2 Line: 4x + y + 3 = 0

> Find the limit (if it exists). If it does not exist, explain why.

> Find an equation of the line that is tangent to the graph of f and parallel to the given line. Function: f(x) = -1/4 x2 Line: x + y = 0

> Find the limit (if it exists). If it does not exist, explain why.

> find the limit (if it exists). If it does not exist, explain why.

> Use the graph to determine each limit, and discuss the continuity of the function. a. / b. / c. /

> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x - 1

> Use the graph to determine each limit, and discuss the continuity of the function. a. / b. / c. /

> In your own words, explain the Intermediate Value Theorem.

> Determine whether / exists. Explain.

> What is the value of c?

> In your own words, describe what it means for a function to be continuous at a point.

> b. Use your answer to part (a) to derive the approximation cos x ≈ 1 – ½ x2 for x near 0. c. Use your answer to part (b) to approximate cos(0.1). d. Use a calculator to approximate cos(0.1) to four decimal places. Compare the result with part (a). /

> Consider f(x) = sec x – 1 / x2 a. Find the domain of f. b. Use a graphing utility to graph f. Is the domain of f obvious from the graph? If not, explain. c. Use the graph of f to approximate / d. Confirm your answer to part (c) analytically.

> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x + 4

> Let

> Prove the second part of Theorem 1.9.

> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.

> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If f(x) = g(x) for all real numbers other than x = 0 and

> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.

> When using a graphing utility to generate a table to approximate a student concluded that the limit was 0.01745 rather than 1. Determine the probable cause of the error.

> Find a function f to show that the converse of Exercise 112 (b) is not true. [Hint: Find a function f such that / │ f(x)│ = │L│ but / f(x) does not exist.]

> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = √x -

> Use the graph shown in the figure. Identify or sketch each of the quantities on the figure. a. f(1) and f(4) b. f(4) â f(1) c. 4 â 1 d. /

> a. Prove that if /│f(x)│ = 0 then /f(x) =0 b. Prove that if / f(x) = L, then / │ f(x)│ = │L│. [Hint: Use the inequality ││f(x)│ − │L││ ≤ │ f(x) − L│.]

> Prove that if / = 0 and │g(x)│≤ M for a fixed number M and all x ≠ c, then / [ f(x)g(x)] = 0.

> Prove that if / = 0 then /

> Prove Property 1 of Theorem 1.2.

> Prove Property 3 of Theorem 1.1. (You may use Property 3 of Theorem 1.2.)

> Prove Property 1 of Theorem 1.1.

> Prove that if / exists and / does not exist, then /does not exist.

> Find two functions f and g such that / and / do not exist, but does exist.

> Use the position function s(t) = â4.9t2 + 200, which gives the height (in meters) of an object that has fallen for t seconds from a height of 200 meters. The velocity at time t = a seconds is given by At what velocity will the object im

> Use the position function s(t) = â4.9t2 + 200, which gives the height (in meters) of an object that has fallen for t seconds from a height of 200 meters. The velocity at time t = a seconds is given by Find the velocity of the object whe

> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = √x, (

> Use the position function s(t) = â16t2 + 500, which gives the height (in feet) of an object that has fallen for t seconds from a height of 500 feet. The velocity at time t = a seconds is given by A construction worker drops a full paint

> Would you use the dividing out technique or the rationalizing technique to find the limit of the function? Explain your reasoning.

> Use a graphing utility to graph f(x) = x, g(x) = sin x, and h(x) = sin x/x in the same viewing window. Compare the magnitudes of f(x) and g(x) when x is close to 0. Use the comparison to write a short paragraph explaining why

> Write a function of each specified type that has a limit of 4 as x approaches 8. a. Linear b. polynomial of degree 2 c. rational d. radical e. cosine f. sine

> a. In the context of finding limits, discuss what is meant by two functions that agree at all but one point. b. Give an example of two functions that agree at all but one point.

> Use a graphing utility to graph the given function and the equations y = ∣x∣ and y = −∣x∣ in the same viewing window. Using the graphs to observe the Squeeze Theorem visually, find / f(x) = x cos 1/x

> Use a graphing utility to graph the given function and the equations y = ∣x∣ and y = −∣x∣ in the same viewing window. Using the graphs to observe the Squeeze Theorem visually, find / f(x) = x sin 1/x

> Use a graphing utility to graph the given function and the equations y = ∣x∣ and y = −∣x∣ in the same viewing window. Using the graphs to observe the Squeeze Theorem visually, find / f(x) = │x│ cos x

> Use a graphing utility to graph the given function and the equations y = ∣x∣ and y = −∣x∣ in the same viewing window. Using the graphs to observe the Squeeze Theorem visually, find / f(x) = │x│ sin x

Question: Find the limit (if it exists). If