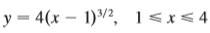Question: Find the length of the curve. /
> (a) Write the solution of the initial-value problem and use it to find the population when t = 20. (b) When does the population reach 1200? dP 0.1P(1 dt P P(0) = 100 2000
> Find the orthogonal trajectories of the family of curves. y = ek*
> Find the orthogonal trajectories of the family of curves. y = ke"
> Solve the initial-value problem y’ = 3x2 ey, y(0) = 1 and graph the solution.
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum. 1/n 1/(n+ R-1
> Identify the curve by finding a Cartesian equation for the curve. r?sin 20 = 1
> Solve the initial-value problem. ху' — у — х In х, у(1) — 2
> Solve the initial-value problem.
> (a) A direction field for the differential equation y’ = y(y-2) (y-4) is shown. Sketch the graphs of the solutions that satisfy the given initial conditions. (b) If the initial condition is y(0) = c, for what values of c is / finite? W
> Find the length of the curve y - i VJi - I di 1<x< 16
> Determine whether the series is absolutely convergent or conditionally convergent. n E (-1)"-1 п? + 4 n-1
> Use Simpson’s Rule with n = 10 to estimate the area of the surface obtained by rotating the sine curve in Exercise 7 about the x-axis. Data from Exercise 7: Use Simpson’s Rule with n = 10 to estimate the length of the sine curve /
> Use series to evaluate the limit. - In(1 + x) lim .2
> (a) The curve y = x2, 0 < x < 1, is rotated about the y-axis. Find the area of the resulting surface. (b) Find the area of the surface obtained by rotating the curve in part (a) about the x-axis.
> Determine whether the sequence converges or diverges. If it converges, find the limit. {sin n}
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum. Σ n + 1
> Let C be the arc of the curve y = 2/(x + 1) from the point (0,2) to (3, 1 2 ). Use a calculator or other device to find the value of each of the following, correct to four decimal places. (a) The length of C (b) The area of the surface obtained by rot
> Identify the curve by finding a Cartesian equation for the curve. r?cos 20 = 1
> (a) Find the length of the curve (b) Find the area of the surface obtained by rotating the curve in part (a) about the y-axis. 1 y = 16 2x? 1<x< 2
> Find the length of the curve. 12х — 4у + Зу 1, 1<у<3 Sy<3
> Evaluate the integral. fe cos x dx
> The length of time spent waiting in line at a certain bank is modeled by an exponential density function with mean 8 minutes. (a) What is the probability that a customer is served in the first 3 minutes? (b) What is the probability that a customer has to
> Lengths of human pregnancies are normally distributed with mean 268 days and standard deviation 15 days. What percentage of pregnancies last between 250 days and 280 days?
> Use integration by parts to prove the reduction formula. tan x sec" 2x п — 2 n | sec"x dx sec" 2x dx (n # 1) 1 п — 1 n -
> (a) Explain why the function is a probability density function. (b) Find P(X (c) Calculate the mean. Is the value what you would expect? TTX sin 20 10 if 0 <x< 10 f(x) if x<0 or x> 10
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. 1 Σ n-1 4 + e"
> After a 6-mg injection of dye into a heart, the readings of dye concentration at two-second intervals are as shown in the table. Use Simpson’s Rule to estimate the cardiac output. c(1) c(1) 14 4.7 1.9 16 3.3 4 3.3 18 2.1 6. 5.1 20
> If the amount of capital that a company has at time t is f(t), then the derivative, f(t), is called the net investment flow. Suppose that the net investment flow is / million dollars per year (where t is measured in years). Find the increase in capital (
> Find the length of the curve. у — 2 In(sin $x), y T/3 <x<T
> Use series to approximate the definite integral to within the indicated accuracy. ro.5 x²e r0.5 x'e *dx (lerror |< 0.001) Jo
> Identify the curve by finding a Cartesian equation for the curve. 0 = 7/3
> Find the Taylor polynomial T3(x) for the function f centered at the number a. Graph f and T3 on the same screen. f(x) = e¯* sin x, a=0
> The demand function for a commodity is given by Find the consumer surplus when the sales level is 100. p= 2000 – 0.1lx – 0.01x²
> Use the Theorem of Pappus and the fact that the volume of a sphere of radius r is / to find the centroid of the semi - circular region bounded by the curve / and the x-axis.
> Find the volume obtained when the circle of radius 1 with center (1, 0) is rotated about the y-axis.
> Find the centroid of the region bounded by the given curves. у — sin x, у— 0, х— п/4, х — Зп/4
> Test the series for convergence or divergence. Vna + 1 Σ n + n 4
> Find the centroid of the region bounded by the given curves. y = }x, y = JE
> Use integration by parts to prove the reduction formula. tan" 'x | tan"x dx | tan" 2x dx (n + 1) n - 1
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum. 3 Σ п(n + 3)
> Find the centroid of the region shown. yA 8 8. -8
> Find the centroid of the region shown. YA (4, 2) 이
> A trough is filled with water and its vertical ends have the shape of the parabolic region in the figure. Find the hydrostatic force on one end of the trough. 8 ft – T 4 ft
> Identify the curve by finding a Cartesian equation for the curve. r = 4 sec 0
> Evaluate the integral. In R dR 22
> A gate in an irrigation canal is constructed in the form of a trapezoid 3 ft wide at the bottom, 5 ft wide at the top, and 2 ft high. It is placed vertically in the canal so that the water just covers the gate. Find the hydrostatic force on one side of t
> Evaluate the integral. (х + 1)? ax
> Determine whether the sequence converges or diverges. If it converges, find the limit. (-1)**'n an n + yn
> Use series to approximate the definite integral to within the indicated accuracy. r0.4 " VI + x* dx (lerror|< 5 × 10 °)
> Evaluate the integral.
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum.
> Evaluate the integral.
> Evaluate the integral.
> Use integration by parts to prove the reduction formula.
> Evaluate the integral.
> Evaluate the integral.
> Identify the curve by finding a Cartesian equation for the curve.
> Determine whether the sequence converges or diverges. If it converges, find the limit.
> Evaluate the integral.
> Evaluate the integral.
> Evaluate the integral.
> Evaluate the integral.
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum.
> Use series to approximate the definite integral to within the indicated accuracy.
> Evaluate the integral.
> Evaluate the integral.
> Evaluate the integral.
> Prove that, for even powers of sine,
> Determine whether the series is convergent or divergent. If it is convergent, find its sum.
> Evaluate the integral.
> Determine whether the series is convergent or divergent.
> Evaluate the integral.
> Evaluate the integral.
> The magnitude of the repulsive force between two point charges with the same sign, one of size 1 and the other of size q, is where r is the distance between the charges and «0 is a constant. The potential V at a point P due to the charge q i
> Determine whether the series is convergent or divergent. If it is convergent, find its sum.
> Use the substitution u = 1/x to show that
> We can extend our definition of average value of a continuous function to an infinite interval by defining the average value off on the interval / (a) Find the average value of y = tan-1 x on the interval / (b) If / is divergent, show that the average va
> Determine whether the sequence converges or diverges. If it converges, find the limit.
> Use series to approximate the definite integral to within the indicated accuracy. "x'arctan x dx (four decimal places)
> Find the area of the region bounded by the curves y = 1/(2 + Jx), y = 1/(2 – Jx), and x = 1.
> Determine whether the series is convergent or divergent. Σ n-1 n
> (a) Use the reduction formula in Example 6 to show that where n > 2 is an integer. (b) Use part (a) to evaluate (c) Use part (a) to show that, for odd powers of sine, w/2 sin"x dx n - п — 1 w/2 sin" 2x dx Jo Sa/? sin'x dx and " sin'x dx. 2·4· 6 ·
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. 3 Σ 5" n
> Find the area of the region bounded by the hyperbola y2 - x2 = 1 and the line y = 3.
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. 2 + sin x - dx 1 (b) dx V1 + x4 (a)
> Determine whether the sequence converges or diverges. If it converges, find the limit. an cos n + 1
> Suppose you are asked to estimate the volume of a football. You measure and find that a football is 28 cm long. You use a piece of string and measure the circumference at its widest point to be 53 cm. The circumference 7 cm from each end is 45Â&nbs
> A population of honeybees increased at a rate of r(t) bees per week, where the graph of r is as shown. Use Simpson’s Rule with six subintervals to estimate the increase in the bee population during the first 24 weeks. 12000 8000 40
> The speedometer reading (v) on a car was observed at 1-minute intervals and recorded in the chart. Use Simpson’s Rule to estimate the distance traveled by the car. I (min) v (mi/h) 1 (min) v (mi/h) 40 56 1 42 7 57 2 45 8 57 3 49 9
> Evaluate the integral. x - 1 x² + 2x
> Evaluate the indefinite integral as an infinite series. S arctan(x²) dx
> If a surveyor measures differences in elevation when making plans for a highway across a desert, corrections must be made for the curvature of the earth. (a) If R is the radius of the earth and L is the length of the highway, show that the correction is
> Estimate the errors involved in Exercise 63, parts (a) and (b). How large should n be in each case to guarantee an error of less than 0.00001? Data from Exercise 63: (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s R
> Test the series for convergence or divergence. 2n TT E (-1)*. (2n)!
> (a) Prove the reduction formula (b) Use part (a) to evaluate (c) Use parts (a) and (b) to evaluate | cos"x dx 1 cos" 'x sin x + п — 1 | cos" ?x dx n ſ cos?x dx. S cos*x dx.
> Determine whether the sequence converges or diverges. If it converges, find the limit. 4" а, 1+ 9"
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its Σ TT
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 10 – 2 + 0.4 – 0.08 + ·
> (a) Explain the difference between (b) Explain the difference between a and ミ E ai E a; and i-1
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain