Question: Use series to approximate the definite integral
Use series to approximate the definite integral to within the indicated accuracy.
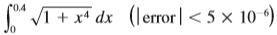
Transcribed Image Text:
r0.4 " VI + x* dx (lerror|< 5 × 10 °)
> Use series to evaluate the limit. 1 lim 1-0 1 e* cos x + x -
> (a) Write the solution of the initial-value problem and use it to find the population when t = 20. (b) When does the population reach 1200? dP 0.1P(1 dt P P(0) = 100 2000
> Find the orthogonal trajectories of the family of curves. y = ek*
> Find the orthogonal trajectories of the family of curves. y = ke"
> Solve the initial-value problem y’ = 3x2 ey, y(0) = 1 and graph the solution.
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum. 1/n 1/(n+ R-1
> Identify the curve by finding a Cartesian equation for the curve. r?sin 20 = 1
> Solve the initial-value problem. ху' — у — х In х, у(1) — 2
> Solve the initial-value problem.
> (a) A direction field for the differential equation y’ = y(y-2) (y-4) is shown. Sketch the graphs of the solutions that satisfy the given initial conditions. (b) If the initial condition is y(0) = c, for what values of c is / finite? W
> Find the length of the curve y - i VJi - I di 1<x< 16
> Determine whether the series is absolutely convergent or conditionally convergent. n E (-1)"-1 п? + 4 n-1
> Use Simpson’s Rule with n = 10 to estimate the area of the surface obtained by rotating the sine curve in Exercise 7 about the x-axis. Data from Exercise 7: Use Simpson’s Rule with n = 10 to estimate the length of the sine curve /
> Use series to evaluate the limit. - In(1 + x) lim .2
> (a) The curve y = x2, 0 < x < 1, is rotated about the y-axis. Find the area of the resulting surface. (b) Find the area of the surface obtained by rotating the curve in part (a) about the x-axis.
> Determine whether the sequence converges or diverges. If it converges, find the limit. {sin n}
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum. Σ n + 1
> Let C be the arc of the curve y = 2/(x + 1) from the point (0,2) to (3, 1 2 ). Use a calculator or other device to find the value of each of the following, correct to four decimal places. (a) The length of C (b) The area of the surface obtained by rot
> Identify the curve by finding a Cartesian equation for the curve. r?cos 20 = 1
> (a) Find the length of the curve (b) Find the area of the surface obtained by rotating the curve in part (a) about the y-axis. 1 y = 16 2x? 1<x< 2
> Find the length of the curve. 12х — 4у + Зу 1, 1<у<3 Sy<3
> Evaluate the integral. fe cos x dx
> The length of time spent waiting in line at a certain bank is modeled by an exponential density function with mean 8 minutes. (a) What is the probability that a customer is served in the first 3 minutes? (b) What is the probability that a customer has to
> Lengths of human pregnancies are normally distributed with mean 268 days and standard deviation 15 days. What percentage of pregnancies last between 250 days and 280 days?
> Use integration by parts to prove the reduction formula. tan x sec" 2x п — 2 n | sec"x dx sec" 2x dx (n # 1) 1 п — 1 n -
> (a) Explain why the function is a probability density function. (b) Find P(X (c) Calculate the mean. Is the value what you would expect? TTX sin 20 10 if 0 <x< 10 f(x) if x<0 or x> 10
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. 1 Σ n-1 4 + e"
> After a 6-mg injection of dye into a heart, the readings of dye concentration at two-second intervals are as shown in the table. Use Simpson’s Rule to estimate the cardiac output. c(1) c(1) 14 4.7 1.9 16 3.3 4 3.3 18 2.1 6. 5.1 20
> If the amount of capital that a company has at time t is f(t), then the derivative, f(t), is called the net investment flow. Suppose that the net investment flow is / million dollars per year (where t is measured in years). Find the increase in capital (
> Find the length of the curve. у — 2 In(sin $x), y T/3 <x<T
> Use series to approximate the definite integral to within the indicated accuracy. ro.5 x²e r0.5 x'e *dx (lerror |< 0.001) Jo
> Identify the curve by finding a Cartesian equation for the curve. 0 = 7/3
> Find the Taylor polynomial T3(x) for the function f centered at the number a. Graph f and T3 on the same screen. f(x) = e¯* sin x, a=0
> The demand function for a commodity is given by Find the consumer surplus when the sales level is 100. p= 2000 – 0.1lx – 0.01x²
> Use the Theorem of Pappus and the fact that the volume of a sphere of radius r is / to find the centroid of the semi - circular region bounded by the curve / and the x-axis.
> Find the volume obtained when the circle of radius 1 with center (1, 0) is rotated about the y-axis.
> Find the centroid of the region bounded by the given curves. у — sin x, у— 0, х— п/4, х — Зп/4
> Test the series for convergence or divergence. Vna + 1 Σ n + n 4
> Find the centroid of the region bounded by the given curves. y = }x, y = JE
> Use integration by parts to prove the reduction formula. tan" 'x | tan"x dx | tan" 2x dx (n + 1) n - 1
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum. 3 Σ п(n + 3)
> Find the centroid of the region shown. yA 8 8. -8
> Find the centroid of the region shown. YA (4, 2) 이
> A trough is filled with water and its vertical ends have the shape of the parabolic region in the figure. Find the hydrostatic force on one end of the trough. 8 ft – T 4 ft
> Identify the curve by finding a Cartesian equation for the curve. r = 4 sec 0
> Evaluate the integral. In R dR 22
> A gate in an irrigation canal is constructed in the form of a trapezoid 3 ft wide at the bottom, 5 ft wide at the top, and 2 ft high. It is placed vertically in the canal so that the water just covers the gate. Find the hydrostatic force on one side of t
> Evaluate the integral. (х + 1)? ax
> Determine whether the sequence converges or diverges. If it converges, find the limit. (-1)**'n an n + yn
> Find the length of the curve. у — 4(х — 1)92, 1<x<4 y
> Evaluate the integral.
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum.
> Evaluate the integral.
> Evaluate the integral.
> Use integration by parts to prove the reduction formula.
> Evaluate the integral.
> Evaluate the integral.
> Identify the curve by finding a Cartesian equation for the curve.
> Determine whether the sequence converges or diverges. If it converges, find the limit.
> Evaluate the integral.
> Evaluate the integral.
> Evaluate the integral.
> Evaluate the integral.
> Determine whether the series is convergent or divergent by expressing sn as a telescoping sum. If it is convergent, find its sum.
> Use series to approximate the definite integral to within the indicated accuracy.
> Evaluate the integral.
> Evaluate the integral.
> Evaluate the integral.
> Prove that, for even powers of sine,
> Determine whether the series is convergent or divergent. If it is convergent, find its sum.
> Evaluate the integral.
> Determine whether the series is convergent or divergent.
> Evaluate the integral.
> Evaluate the integral.
> The magnitude of the repulsive force between two point charges with the same sign, one of size 1 and the other of size q, is where r is the distance between the charges and «0 is a constant. The potential V at a point P due to the charge q i
> Determine whether the series is convergent or divergent. If it is convergent, find its sum.
> Use the substitution u = 1/x to show that
> We can extend our definition of average value of a continuous function to an infinite interval by defining the average value off on the interval / (a) Find the average value of y = tan-1 x on the interval / (b) If / is divergent, show that the average va
> Determine whether the sequence converges or diverges. If it converges, find the limit.
> Use series to approximate the definite integral to within the indicated accuracy. "x'arctan x dx (four decimal places)
> Find the area of the region bounded by the curves y = 1/(2 + Jx), y = 1/(2 – Jx), and x = 1.
> Determine whether the series is convergent or divergent. Σ n-1 n
> (a) Use the reduction formula in Example 6 to show that where n > 2 is an integer. (b) Use part (a) to evaluate (c) Use part (a) to show that, for odd powers of sine, w/2 sin"x dx n - п — 1 w/2 sin" 2x dx Jo Sa/? sin'x dx and " sin'x dx. 2·4· 6 ·
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. 3 Σ 5" n
> Find the area of the region bounded by the hyperbola y2 - x2 = 1 and the line y = 3.
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. 2 + sin x - dx 1 (b) dx V1 + x4 (a)
> Determine whether the sequence converges or diverges. If it converges, find the limit. an cos n + 1
> Suppose you are asked to estimate the volume of a football. You measure and find that a football is 28 cm long. You use a piece of string and measure the circumference at its widest point to be 53 cm. The circumference 7 cm from each end is 45Â&nbs
> A population of honeybees increased at a rate of r(t) bees per week, where the graph of r is as shown. Use Simpson’s Rule with six subintervals to estimate the increase in the bee population during the first 24 weeks. 12000 8000 40
> The speedometer reading (v) on a car was observed at 1-minute intervals and recorded in the chart. Use Simpson’s Rule to estimate the distance traveled by the car. I (min) v (mi/h) 1 (min) v (mi/h) 40 56 1 42 7 57 2 45 8 57 3 49 9
> Evaluate the integral. x - 1 x² + 2x
> Evaluate the indefinite integral as an infinite series. S arctan(x²) dx
> If a surveyor measures differences in elevation when making plans for a highway across a desert, corrections must be made for the curvature of the earth. (a) If R is the radius of the earth and L is the length of the highway, show that the correction is
> Estimate the errors involved in Exercise 63, parts (a) and (b). How large should n be in each case to guarantee an error of less than 0.00001? Data from Exercise 63: (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s R
> Test the series for convergence or divergence. 2n TT E (-1)*. (2n)!
> (a) Prove the reduction formula (b) Use part (a) to evaluate (c) Use parts (a) and (b) to evaluate | cos"x dx 1 cos" 'x sin x + п — 1 | cos" ?x dx n ſ cos?x dx. S cos*x dx.
> Determine whether the sequence converges or diverges. If it converges, find the limit. 4" а, 1+ 9"
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its Σ TT
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 10 – 2 + 0.4 – 0.08 + ·
> (a) Explain the difference between (b) Explain the difference between a and ミ E ai E a; and i-1

