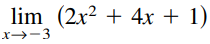Question: Find the limit. /
> Find the limit.
> Find the limit.
> Find the derivative of the function by the limit process. h(s) = -2√s
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Find the derivative of the function by the limit process. f(x) = √x + 4
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the derivative of the function by the limit process. f(x) = 1/x2
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limits. f(x) = 2x2 − 3x + 1, g(x) =∛x + 6 a. / b. / c. /
> Find the limits. a. / b. / c. /
> Find the limits. f(x) = x + 7, g(x) = x2 a. / b. / c. /
> Find the limits. f(x) = 5 − x, g(x) = x3 a. / b. / c. /
> Find the derivative of the function by the limit process. f(x) = 1 / x − 1
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the derivative of the function by the limit process. g(t) = t3 + 4t
> Estimate the slope of the graph at the points (x1, y1) and (x2, y2).
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> List the two special trigonometric limits.
> In your own words, explain the Squeeze Theorem.
> Find the derivative of the function by the limit process. f(x) = x3 − 12x
> What is meant by an indeterminate form?
> Describe how to find the limit of a polynomial function p(x) as x approaches c.
> A right circular cone has base of radius 1 and height 3. A cube is inscribed in the cone so that one face of the cube is contained in the base of the cone. What is the side-length of the cube?
> Inscribe a rectangle of base b and height h in a circle of radius one, and inscribe an isosceles triangle in a region of the circle cut off by one base of the rectangle (with that side as the base of the triangle). For what value of h do the rectangle an
> Given that prove that there exists an open interval (a, b) containing 0 such that (3x + 1)(3x − 1)x2 + 0.01 > 0 for all x ≠0 in (a, b). / exists an open interval (a, b) containing c such that g(x) > 0 for all x
> Prove that is equivalent to
> Consider the line f(x) = mx + b, where m ≠ 0. Use the ε-δ definition of limit to prove that / f(x) = mc + b.
> Prove that if the limit of f(x) as x approaches c exists, then the limit must be unique. [Hint: Let / f(x) = L1 and / f(x) = L2 and prove that L1 = L2.]
> Use a graphing utility to evaluate for several values of n. What do you notice?
> Use a graphing utility to evaluate for several values of n. What do you notice?
> Find the derivative of the function by the limit process. f(x) = x2 − 5
> Consider the function f(x) = √x.
> Consider the function f(x) = √x.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If the limit of f(x) as x approaches c is 0, then there must exist a number k such that f(k) < 0.001.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If f is undefined at x = c, then the limit of f(x) as x approaches c does not exist.
> Use the graph of f to identify the values of c for which / f(x) exists. a. / b. /
> The statement means that for each ε > 0 there corresponds a δ > 0 such that if 0 If ε = 0.001, then Use a graphing utility to graph each side of this inequality. Use the zoom feature to find an interval (2 &ac
> Consider the function Estimate by evaluating f at x-values near 0. Sketch the graph of f.
> Consider the function f(x) = (1 + x)1/x Estimate by evaluating f at x-values near 0. Sketch the graph of f.
> Find the derivative of the function by the limit process. f(x) = x2 + x – 3
> A sporting goods manufacturer designs a golf ball having a volume of 2.48 cubic inches. a. What is the radius of the golf ball? b. The volume of the golf ball varies between 2.45 cubic inches and 2.51 cubic inches. How does the radius vary? c. Use the ε-
> A jeweler resizes a ring so that its inner circumference is 6 centimeters. a. What is the radius of the ring? b. The inner circumference of the ring varies between 5.5 centimeters and 6.5 centimeters. How does the radius vary? c. Use the ε-δ definit
> If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain your reasoning.
> If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2? Explain your reasoning.
> The definition of limit requires that f is a function defined on an open interval containing c, except possibly at c. Why is this requirement necessary?
> When using the definition of limit to prove that L is the limit of f(x) as x approaches c, you find the largest satisfactory value of δ. Why would any smaller positive value of δ also work?
> For a long-distance phone call, a hotel charges $5.79 for the first minute and $0.99 for each additional minute or fraction thereof. A formula for the cost is given by C(t) = 5.79 − 0.99[1 – t], t > 0 where t is the time in minutes. (Note: [x] = greatest
> For a long-distance phone call, a hotel charges $9.99 for the first minute and $0.79 for each additional minute or fraction thereof. A formula for the cost is given by C(t) = 9.99 − 0.79⟨1 − t⟩, t > 0 where t is the time in minutes. (Note: [x] = greatest
> Use a graphing utility to graph the function and estimate the limit (if it exists). What is the domain of the function? Can you detect a possible error in determining the domain of a function solely by analyzing the graph generated by a graphing utility?
> Use a graphing utility to graph the function and estimate the limit (if it exists). What is the domain of the function? Can you detect a possible error in determining the domain of a function solely by analyzing the graph generated by a graphing utility?
> Find the derivative of the function by the limit process. f(x) = 5 – 2/3 x
> What is the limit of g(x) = x as x approaches π?
> What is the limit of f(x) = 4 as x approaches π?
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.