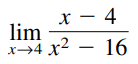Question: Find the limit. /
> Use a graphing utility to graph the given function and the equations y = ∣x∣ and y = −∣x∣ in the same viewing window. Using the graphs to observe the Squeeze Theorem visually, find / f(x) = │x│ sin x
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x3 +
> Use the Squeeze Theorem to find / c = a b − │x − a│≤ f(x) ≤ b + ∣x − a∣
> Use the Squeeze Theorem to find / c = 0 4 − x2 ≤ f(x) ≤ 4 + x2
> Find /
> Find /
> Find /
> Find /
> Find /
> Find /
> Find /
> Find /
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x3 ,
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x2 +
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x2 +
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the derivative of the function by the limit process. h(s) = -2√s
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Find the derivative of the function by the limit process. f(x) = √x + 4
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the derivative of the function by the limit process. f(x) = 1/x2
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limits. f(x) = 2x2 − 3x + 1, g(x) =∛x + 6 a. / b. / c. /
> Find the limits. a. / b. / c. /
> Find the limits. f(x) = x + 7, g(x) = x2 a. / b. / c. /
> Find the limits. f(x) = 5 − x, g(x) = x3 a. / b. / c. /
> Find the derivative of the function by the limit process. f(x) = 1 / x − 1
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the derivative of the function by the limit process. g(t) = t3 + 4t
> Estimate the slope of the graph at the points (x1, y1) and (x2, y2).
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> List the two special trigonometric limits.
> In your own words, explain the Squeeze Theorem.