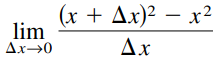Question: Find the limit. /
> Use the position function s(t) = −4.9t2 + 200, which gives the height (in meters) of an object that has fallen for t seconds from a height of 200 meters. The velocity at time t = a seconds is given by At what velocity will the object im
> Use the position function s(t) = −4.9t2 + 200, which gives the height (in meters) of an object that has fallen for t seconds from a height of 200 meters. The velocity at time t = a seconds is given by Find the velocity of the object whe
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = √x, (
> Use the position function s(t) = −16t2 + 500, which gives the height (in feet) of an object that has fallen for t seconds from a height of 500 feet. The velocity at time t = a seconds is given by A construction worker drops a full paint
> Use the position function s(t) = −16t2 + 500, which gives the height (in feet) of an object that has fallen for t seconds from a height of 500 feet. The velocity at time t = a seconds is given by A construction worker drops a full paint
> Would you use the dividing out technique or the rationalizing technique to find the limit of the function? Explain your reasoning.
> Use a graphing utility to graph f(x) = x, g(x) = sin x, and h(x) = sin x/x in the same viewing window. Compare the magnitudes of f(x) and g(x) when x is close to 0. Use the comparison to write a short paragraph explaining why
> Write a function of each specified type that has a limit of 4 as x approaches 8. a. Linear b. polynomial of degree 2 c. rational d. radical e. cosine f. sine
> a. In the context of finding limits, discuss what is meant by two functions that agree at all but one point. b. Give an example of two functions that agree at all but one point.
> Use a graphing utility to graph the given function and the equations y = ∣x∣ and y = −∣x∣ in the same viewing window. Using the graphs to observe the Squeeze Theorem visually, find / f(x) = x cos 1/x
> Use a graphing utility to graph the given function and the equations y = ∣x∣ and y = −∣x∣ in the same viewing window. Using the graphs to observe the Squeeze Theorem visually, find / f(x) = x sin 1/x
> Use a graphing utility to graph the given function and the equations y = ∣x∣ and y = −∣x∣ in the same viewing window. Using the graphs to observe the Squeeze Theorem visually, find / f(x) = │x│ cos x
> Use a graphing utility to graph the given function and the equations y = ∣x∣ and y = −∣x∣ in the same viewing window. Using the graphs to observe the Squeeze Theorem visually, find / f(x) = │x│ sin x
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x3 +
> Use the Squeeze Theorem to find / c = a b − │x − a│≤ f(x) ≤ b + ∣x − a∣
> Use the Squeeze Theorem to find / c = 0 4 − x2 ≤ f(x) ≤ 4 + x2
> Find /
> Find /
> Find /
> Find /
> Find /
> Find /
> Find /
> Find /
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x3 ,
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x2 +
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> (a) Find an equation of the tangent line to the graph of f at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results. f(x) = x2 +
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the derivative of the function by the limit process. h(s) = -2√s
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Find the derivative of the function by the limit process. f(x) = √x + 4
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Write a simpler function that agrees with the given function at all but one point. Then find the limit of the function. Use a graphing utility to confirm your result.
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Use the information to evaluate the limits. a. / b. / c. / d. /
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the derivative of the function by the limit process. f(x) = 1/x2
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limit of the trigonometric function.
> Find the limits. f(x) = 2x2 − 3x + 1, g(x) =∛x + 6 a. / b. / c. /
> Find the limits. a. / b. / c. /
> Find the limits. f(x) = x + 7, g(x) = x2 a. / b. / c. /
> Find the limits. f(x) = 5 − x, g(x) = x3 a. / b. / c. /
> Find the derivative of the function by the limit process. f(x) = 1 / x − 1
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.