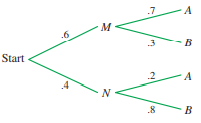
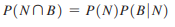[SOLVED] Find the probabilities by referring to the

> Find each limit if it exists.

> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of drawing 1 card from a standard 52-card deck , what is the probability of drawing. Figure 4: A red queen.

> Find each limit if it exists.

> Use the graph of the function f shown to estimate the indicated limits and function values.

> Use the graph of the function g shown to estimate the indicated limits and function values.

> Use the graph of the function f shown to estimate the indicated limits and function values.

> A single card is drawn from a standard 52-card deck. Let D be the event that the card drawn is a diamond, and let F be the event that the card drawn is a face card. find the indicated probabilities.

> Write the expression as a quotient of integers, reduced to lowest terms.

> Use the graph of the function f shown to estimate the indicated limits and function values.

> You draw and keep a single bill from a hat that contains a $1, $10, $20, $50, and $100 bill. What is the expected value of the game to you?

> If the probability distribution for the random variable X is given in the table, what is the expected value of X?

> Find the average (mean) of the exam scores in Problem 2, if each score is divided by 2.

> Find the average (mean) of the exam scores in Problem 2, if 3 points are subtracted from each score.

> Find the average (mean) of the exam scores 78, 64, 97, 60, 86, and 83.

> Repeat Problem 55, assuming that the Grand Prize is currently $400,000,000. Data from Problem 55: A $2 Powerball lottery ticket has a 1/27.05 prob- 2. (A) ability of winning $4, a 1/317.39 probability of winning $7, a 1/10,376.47 probability of winning

> A pink-flowering plant is of genotype RW. If two such plants are crossed, we obtain a red plant (RR) with probability .25, a pink plant (RW or WR) with probability .50, and a white plant (WW) with probability .25, as shown in the table. What is the expec

> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of drawing 1 card from a standard 52-card deck , what is the probability of drawing. Figure 4: An ace.

> Repeat Problem 51, assuming that additional analysis caused the estimated probability of success in field B to be changed from .1 to .11. Data from Problem 51: After careful testing and analysis, an oil company is considering drilling in two different s

> An insurance company charges an annual premium of $75 for a $200,000 insurance policy against a house burning down. If the (empirical) probability that a house burns down in a given year is .0003, what is the expected value of the policy to the insurance

> A 3-card hand is dealt from a standard deck. You win $100 for each king in the hand. If the game is fair, how much should you lose if the hand contains no kings?

> Use a graphing calculator to simulate the results of placing a $1 bet on black in each of 400 games of roulette and compare the simulated and expected gains or losses.

> Repeat Problem 43 with the purchase of 10 tickets. Data from Problem 43: One thousand raffle tickets are sold at $1 each. Three tickets will be drawn at random (without replacement), and each will pay $200. Suppose you buy 5 tickets. (A) Create a payof

> A box of 8 flashbulbs contains 3 defective bulbs. A random sample of 2 is selected and tested. Let X be the random variable associated with the number of defective bulbs in a sample. (A) Find the probability distribution of X. (B) Find the expected num

> Ten thousand raffle tickets are sold at $2 each for a local library benefit. Prizes are awarded as follows: 2 prizes of $1,000, 4 prizes of $500, and 10 prizes of $100. What is the expected value of this raffle if you purchase 1 ticket?

> A game has an expected value to you of - $0.50. It costs $2 to play, but if you win, you receive $20 (including your $2 bet) for a net gain of $18. What is the probability of winning? Would you play this game? Discuss the factors that would influence you

> In roulette (see Problem 35), the numbers from 1 to 36 are evenly divided between red and black. A player who bets $1 on black wins $1 (and gets the $1 bet back) if the ball comes to rest on black; otherwise (if the ball lands on red, 0, or 00), the $1 b

> The payoff table for three possible courses of action is given below. Which of the three actions will produce the largest expected value? What is it?

> A single card is drawn from a standard 52-card deck. Let D be the event that the card drawn is a diamond, and let F be the event that the card drawn is a face card. find the indicated probabilities.

> A 5-card hand is dealt from a standard 52-card deck. If the hand contains at least one diamond, you win $10; otherwise, you lose $4. What is the expected value of the game?

> A card is drawn from a standard 52-card deck. If the card is a diamond, you win $10; otherwise, you lose $4. What is the expected value of the game?

> A coin is tossed three times. Suppose you lose $3 if 3 heads appear, lose $2 if 2 heads appear, and win $3 if 0 heads appear. How much should you win or lose if 1 head appears in order for the game to be fair?

> A single die is rolled once. You lose $12 if a number divisible by 3 turns up. How much should you win if a number not divisible by 3 turns up in order for the game to be fair? Describe the process and reasoning used to arrive at your answer.

> On three rolls of a single die, you will lose $10 if a 5 turns up at least once, and you will win $7 otherwise. What is the expected value of the game?

> In Problem 21, for the game to be fair, how much should you lose if a head and a tail turn up? Data from Problem 21: Two coins are flipped. You win $2 if either 2 heads or 2 tails turn up; you lose $3 if a head and a tail turn up. What is the expected v

> Repeat Problem 19 with the same game costing $3.50 for each play. Data from Problem 19: After paying $4 to play, a single fair die is rolled, and you are paid back the number of dollars corresponding to the number of dots facing up. For example, if a 5

> Repeat Problem 17, assuming an unfair coin with the probability of a head being .55 and a tail being .45 Data from Problem 17: A fair coin is flipped. If a head turns up, you win $1. If a tail turns up, you lose $1. What is the expected value of the gam

> In a family with 2 children, excluding multiple births and assuming that a boy is as likely as a girl at each birth, what is the expected number of boys?

> You draw a single card from a standard 52-card deck. If it is an ace, you win $104. Otherwise you get nothing. What is the expected value of the game to you?

> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of drawing 1 card from a standard 52-card deck , what is the probability of drawi, Figure 4: A numbered card.

> You draw and keep a single coin from a bowl that contains 120 nickels and 80 quarters. What is the expected value of the game to you?

> write each expression as a quotient of integers, reduced to lowest terms.

> In a given county, records show that of the registered voters, 45% are Democrats, 35% are Republicans, and 20% are independents. In an election, 70% of the Democrats, 40% of the Republicans, and 80% of the independents voted in favor of a parks and recre

> A test for tuberculosis was given to 1,000 subjects, 8% of whom were known to have tuberculosis. For the subjects who had tuberculosis, the test indicated tuberculosis in 90% of the subjects, was inconclusive for 7%, and indicated no tuberculosis in 3%.

> In a random sample of 200 women who suspect that they are pregnant, 100 turn out to be pregnant. A new pregnancy test given to these women indicated pregnancy in 92 of the 100 pregnant women and in 12 of the 100 nonpregnant women. If a woman suspects she

> A store sells three types of flash drives: brand A, brand B, and brand C. Of the flash drives it sells, 60% are brand A, 25% are brand B, and 15% are brand C. The store has found that 20% of the brand A flash drives, 15% of the brand B flash drives, and

> A company has rated 75% of its employees as satisfactory and 25% as unsatisfactory. Personnel records indicate that 80% of the satisfactory workers had previous work experience, while only 40% of the unsatisfactory workers had any previous work experienc

> A single card is drawn from a standard 52-card deck. Let D be the event that the card drawn is a diamond, and let F be the event that the card drawn is a face card. find the indicated probabilities.

> If U1 and U2 are two mutually exclusive events whose union is the equally likely sample space S and if E is an arbitrary event in S such that P(E)(0, show that

> a player is dealt two cards from a 52-card deck. If the first card is black, the player returns it to the deck before drawing the second card. If the first card is red, the player sets it aside and then draws the second card. If the second card drawn is

> a player is dealt two cards from a 52-card deck. If the first card is black, the player returns it to the deck before drawing the second card. If the first card is red, the player sets it aside and then draws the second card. What is the probability of d

> A box contains 10 balls numbered 1 through 10. Two balls are drawn in succession without replacement. If the second ball drawn has the number 4 on it, what is the probability that the first ball had a smaller number on it? An even number on it?

> Two balls are drawn in succession from an urn containing m blue balls and n white balls (m â¥ 2 and n â¥ 2). Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexamp

> Refer to the following probability tree: Suppose that c = d = e = f . Discuss the dependence or independence of events M and N.

> urn 1 contains 7 red and 3 white balls. Urn 2 contains 4 red and 5 white balls. A ball is drawn from urn 1 and placed in urn 2. Then a ball is drawn from urn 2. If the ball drawn from urn 2 is white, what is the probability that the ball drawn from urn

> An urn contains 4 red and 5 white balls. Two balls are drawn in succession without replacement. If the second ball is red, what is the probability that the first ball was red?

> one of two urns is chosen at random, with one as likely to be chosen as the other. Then a ball is withdrawn from the chosen urn. Urn 1 contains 1 white and 4 red balls, and urn 2 has 3 white and 2 red balls. If a red ball is drawn, what is the probabili

> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of drawing 1 card from a standard 52-card deck , what is the probability of drawing. Figure 4: A black card.

> one of two urns is chosen at random, with one as likely to be chosen as the other. Then a ball is withdrawn from the chosen urn. Urn 1 contains 1 white and 4 red balls, and urn 2 has 3 white and 2 red balls. If a white ball is drawn, what is the probabi

> Use the probabilities in the first tree diagram to find the probability of each branch of the second tree diagram.

> Find the probabilities by referring to the tree diagram below. P(B | D)

> Find the probabilities by referring to the tree diagram below. P(D)

> Find the probabilities by referring to the tree diagram below. P(B)

> Find the probabilities by referring to the following tree diagram and using Bayesâ formula. Round answers to three decimal places. P(W|Câ²)

> Find the probabilities by referring to the following tree diagram and using Bayesâ formula. Round answers to three decimal places. P(U|Câ²)

> Find the probabilities by referring to the following tree diagram and using Bayesâ formula. Round answers to three decimal places. P(V|Câ²)

> Find the probabilities referring to the following Venn diagram and using Bayesâ formula (assume that the simple events in S are equally likely): P(U2 | Râ)

> Find the probabilities referring to the following Venn diagram and using Bayesâ formula (assume that the simple events in S are equally likely): P(U2 | R)

> A single card is drawn from a standard 52-card deck. Let D be the event that the card drawn is a diamond, and let F be the event that the card drawn is a face card. find the indicated probabilities.

> Find the probabilities by referring to the tree diagram below.

> Use a tree diagram to represent a factorization of the given integer into primes, so that there are two branches at each number that is not prime. For example, the factorization 24 = 4 â 6 = (2 â 2) (2â&#15

> Refer to the data in the following table, obtained in a study to determine the frequency and dependency of IQ ranges relative to males and females. 1,000 people were chosen at random and the following results were recorded: (A) What is the probability o

> In a study to determine frequency and dependency of color-blindness relative to females and males, 1,000 people were chosen at random, and the following results were recorded: (A) Convert this table to a probability table by dividing each entry by 1,0

> To transfer into a particular technical department, a company requires an employee to pass a screening test. A maximum of 3 attempts are allowed at 6-month intervals between trials. From past records it is found that 40% pass on the first trial; of those

> An automobile manufacturer produces 37% of its cars at plant A. If 5% of the cars manufactured at plant A have defective emission control devices, what is the probability that one of this manufacturer’s cars was manufactured at plant A and has a defectiv

> Show that P(A|B) = 1 if B is a subset of A and P(B) ∙ 0.

> A circular spinner is divided into 15 sectors of equal area: 6 red sectors, 5 blue, 3 yellow, and 1 green. , consider the experiment of spinning the spinner once. Find the probability that the spinner lands on: Purple.

> Show that P(A|B) + P(A′|B) = 1.

> Show that if A and B are events with nonzero probabilities in a sample space S, and either P(A|B) = P(A) or P(B|A) = P(B), then events A and B are independent.

> Ann and Barbara are playing a tennis match. The first player to win 2 sets wins the match. For any given set, the probability that Ann wins that set is 2/ 3. Find the probability that (A) Ann wins the match. (B) 3 sets are played. (C) The player who w

> For the experiment in Problem 71, what is the probability that no white balls are drawn? Data from problem71: A box contains 2 red, 3 white, and 4 green balls. Two balls are drawn out of the box in succession without replacement. What is the probability

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample.

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counter example.

> Refer to the following experiment: 2 balls are drawn in succession out of a box containing 2 red and 5 white balls. Let Ri be the event that the ith ball is red, and let Wi be the event that the ith ball is white. Find the probability that both balls wer

Question: Find the probabilities by referring to the