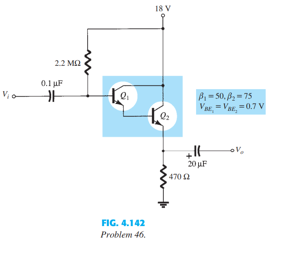
Question: For the Darlington amplifier of Fig. 4.
For the Darlington amplifier of Fig. 4.142 determine
a. the level of ï¢D.
b. the base current of each transistor.
c. the collector current of each transistor.
d. the voltages VC1, VC2, VE1, and VE2.
> Define the region of operation for the JFET of Fig. 6.54 if
> For the 2N5457 JFET of Fig. 6.20, what is the power rating at a typical operating temperature of 45°C using the 5.0 mW/°C derating factor.
> Define the region of operation for the 2N5457 JFET of Fig. 6.20 using the range of IDSS and VP provided. That is, sketch the transfer curve defined by the maximum IDSS and VP and the transfer curve for the minimum IDSS and VP. Then, shade in the resultin
> A p-channel JFET has device parameters of IDSS = 7.5 mA and VP = 4 V. Sketch the transfer characteristics.
> Calculate collector currents for Q1 and Q2 in Fig. 4.146.
> Using the characteristics of Fig. 6.11: a. Determine the difference in drain current (for VDS 7 VP) between VGS = 0 V and VGS = -1 V. b. Repeat part (a) between VGS = -1 and -2 V. •312Repeat part (a) between VGS = -2 and -3 V. c. Repeat part (a) between
> Given the network of Fig. 5.190: a. Is the network properly biased? b. What problem in the network construction could cause VB to be 6.22 V and obtain the given waveform of Fig. 5.190?
> a. Based on a review of the characteristics of Fig. 5.126, which parameter changed the most with increase in temperature? b. Which changed the least? c. What are the maximum and minimum values of hfe? Is the change in magnitude significant? Was it expect
> a. Based on a review of the characteristics of Fig. 5.124, which parameter changed the least for the full range of collector current? b. Which parameter changed the most? c. What are the maximum and minimum values of 1>hoe? Is the approximation 1>hoe ǁ R
> a. If hre = 2 * 10-4 at IC = 1 mA on Fig. 5.124, determine the approximate value of hre at 0.1 mA. b. For the value of hre determined in part (a), can hre be ignored as a good approximation if Av = 210?
> a. If hoe = 20 mS at IC = 1 mA of Fig. 5.124, what is the approximate value of hoe at IC = 10 mA? b. Determine its resistive value at 10 mA and compare to a resistive load of 6.8 kΩ. Is it a good approximation to ignore the effects of 1>hoe in this case?
> a. If hoe = 20 mS at IC = 1 mA on Fig. 5.124, what is the approximate value of hoe at IC = 0.2 mA? b. Determine its resistive value at 0.2 mA and compare to a resistive load of 6.8 kΩ. Is it a good approximation to ignore the effects of 1>hoe in this cas
> Repeat Problem 74 for hie (same changes in IC).
> a. Using Fig. 5.124, determine the magnitude of the percentage change in hfe for an IC change from 0.2 mA to 1 mA using the equation b. Repeat part (a) for an IC change from 1 mA to 5 mA.
> Given a Q-point of IDQ = 3 mA and VGS = - 3 V, determine IDSS if VP = - 6 V.
> For the common-base amplifier of Fig. 5.189, determine: a. Zi. b. Ai. c. Av. d. Zo.
> Calculate the mirrored current I in the circuit of Fig. 4.145.
> For the network of Fig. 5.188, determine: a. Zi. b. Av. c. Ai=Io>Ii. d. Zo.
> Repeat parts (a) and (b) of Problem 68 with hre = 2 * 10-4 and compare results.
> For the common-base network of Fig. 5.187: a. Determine Zi and Zo. b. Calculate Av and Ai. c. Determine a, b, re, and ro.
> For the network of Fig. 5.186: a. Determine Zi and Zo. b. Calculate Av and Ai. c. Determine re and compare bre to hie.
> For the network of Problem 11: a. Determine re. b. Find hfe and hie. c. Find Zi and Zo using the hybrid parameters. d. Calculate Av and Ai using the hybrid parameters. e. Determine Zi and Zo if hoe = 50 mS. f. Determine Av and Ai if hoe = 50 mS. g. Compa
> a. Given b = 120, re = 4.5 Ω, and ro = 40 kΩ, sketch the approximate hybrid equivalent circuit. b. Given hie = 1 kΩ, hre = 2 * 10-4, hfe = 90, and hoe = 20 mS, sketch the re model.
> Repeat Problem 63 for RL = 3.3 kΩ and the average value of hoe in Fig. 5.92.
> Repeat Problem 62 using the average values of the parameters of Fig. 5.92 with Av = - 180.
> Given the typical values of RL = 2.2 kΩ and hoe = 20 mS, is it a good approximation to ignore the effects of 1>hoe on the total load impedance? What is the percentage difference in total loading on the transistor using the followin
> Given the typical values of hie = 1 kΩ, hre = 2 * 10-4, and Av = - 160 for the input con- figuration of Fig. 5.185:
> For the feedback amplifier of Fig. 4.144 determine a. the base and collector current of each transistor. b. the base, emitter, and collector voltages of each transistor.
> Given IDSS = 6 mA and VP = - 4.5 V: a. Determine ID at VGS = - 2 and - 3.6 V. b. Determine VGS at ID = 3 and 5.5 mA.
> For a particular JFET if ID = 4 mA when VGS = —3 V, determine VP if IDSS = 12 mA.
> Given IDSS = 16 mA and VP = - 5 V, sketch the transfer characteristics using the data points of Table 6.1. Determine the value of ID at VGS = - 3 V from the curve, and compare it to the value determined using Shockley’s equation. Repeat the above for VGS
> Given IDSS = 9 mA and VP = - 4 V, determine ID when: a. VGS = 0 V. b. VGS = -2 V. c. VGS = -4 V. d. VGS = -6 V.
> Given IE (dc) = 1.2 mA, b = 120 and ro = 40 kΩ, sketch the following: a. Common-emitter hybrid equivalent model. b. Common-emitter re equivalent model. c. Common-base hybrid equivalent model. d. Common-base re equivalent model.
> Repeat problem 54 if a load resistance of 1.2 kΩ is introduced.
> Repeat problem 54 if a 22-Ω resistor is added between VE2 and ground.
> For the feedback pair of Fig. 5.182: a. Calculate the dc voltages VB1, VB2, VC1, VC2, VE1, and VE2. b. Determine the dc currents IB1, IC1, IB2, IC2, and IE2. c. Calculate the impedances Zi and Zo. d. Find the voltage gain Av = VO>VI. e. Determine the
> a. Given IDSS = 12 mA and VP = - 4 V, sketch the transfer characteristics for the JFET transistor. b. Sketch the drain characteristics for the device of part (a).
> Determine Av = VO>Vs for the network of Fig. 5.181 if the source has an internal resistance of 1.2 kΩ and the applied load is 10 kΩ.
> For the cascode amplifier of Fig. 4.143 determine a. the base and collector currents of each transistor. b. the voltages VB1, VB2, VE1, VC1, VE2, and VC2.
> Repeat problem 50 with a load resistor of 1.2 kΩ.
> For the Darlington network of Fig. 5.181: a. Determine the dc levels of VB1, VC1, VE2, VCB1, and VCE2. b. Find the currents IB1, IB2, and IE2. c. Calculate Zi and Zo. d. Determine the voltage gain Av = Vo/Vi and current gain Ai = Io>Ii.
> Calculate the ac voltage across a 10-kΩ load connected at the output of the circuit in Fig. 5.180.
> For the cascode amplifier circuit of Fig. 5.180, calculate the voltage gain Av and output voltage Vo.
> For the cascode amplifier circuit of Fig. 5.180, calculate the dc bias voltages VB1, VB2, and VC2.
> a. Calculate the voltage gain of each stage and the overall ac voltage gain for the BJT cascade amplifier circuit of Fig. 5.179. b. Find AiT = Io>Ii.
> For the BJT cascade amplifier of Fig. 5.179, calculate the dc bias voltages and collector current for each stage
> For the cascaded system of Fig. 5.178, determine: a. The loaded voltage gain of each stage. b. The total gain of the system, AvL and Avs. c. The loaded current gain of each stage. d. The total current gain of the system. e. How Zi is affected by the seco
> For the cascaded system of Fig. 5.177 with two identical stages, determine: a. The loaded voltage gain of each stage. b. The total gain of the system, Av and Avs. c. The loaded current gain of each stage. d. The total current gain of the system AiL=Io>
> Sketch the transfer characteristics of a p-channel enhancement-type MOSFET if VT = - 5 V and k = 0.45 * 10-3 A>V2.
> Does the current of an enhancement-type MOSFET increase at about the same rate as a depletion- type MOSFET for the conduction region? Carefully review the general format of the equations, and if your mathematics background includes differential calculus,
> The maximum drain current for the 2N4351 n-channel enhancement-type MOSFET is 30 mA. Determine VGS at this current level if k = 0.06 * 10-3 A>V2 and VT is the maximum value.
> a. Determine the voltage gain AvL for the network of Fig. 5.173 with RL = 4.7 kΩ, 2.2 kΩ, and 0.5 kΩ. What is the effect of decreasing levels of RL on the voltage gain? b. How will Zi, Zo, and AvNL change with decreasing levels of RL?
> Given the transfer characteristics of Fig. 6.55, determine VT and k and write the general equation for ID.
> a. Given VGS (Th) = 4 V and ID(on) = 4 mA at VGS(on) = 6 V, determine k and write the general expression for ID in the format of Eq. (6.15). b. Sketch the transfer characteristics for the device of part (a). c. Determine ID for the device of part (a) at
> a. Sketch the transfer and drain characteristics of an n-channel enhancement-type MOSFET if VT = 3.5 V and k = 0.4 * 10-3 A>V2. b. Repeat part (a) for the transfer characteristics if VT is maintained at 3.5 V but k is increased by 100% to 0.8 *10-3 A>V2.
> a. Determine the voltage gain AvL for the network of Fig. 5.170 for RL = 4.7 kΩ, 2.2 kΩ, and 0.5 kΩ. What is the effect of decreasing levels of RL on the voltage gain? b. How will Zi, Zo, and AvNL change with decreasing values of RL?
> If the drain current for the 2N3797 MOSFET of Fig. 6.31 is 8 mA, what is the maximum permissible value of VDS utilizing the maximum power rating?
> Repeat problem 32 with the addition of an emitter resistor RE = 0.68 kΩ.
> For the network of Fig. 5.169: a. Determine Zi and Zo. b. Find Av.
> For the R–C-coupled amplifier of Fig. 4.141 determine a. the voltages VB, VC, and VE for each transistor. b. the currents IB, IC, and IE for each transistor
> For the network of Fig. 5.49: a. Derive the approximate equation for Av. b. Derive the approximate equations for Zi and Zo. c. Given RC = 2.2 kΩ, RF = 120 kΩ, RE = 1.2 kΩ, b = 90, and VCC = 10 V, calculate the magnitudes of Av, Zi, and Zo using the equat
> Given re = 10 Ω, b = 200, Av = - 160, and Ai = 19 for the network of Fig. 5.168, deter- mine RC, RF, and VCC.
> For the collector feedback configuration of Fig. 5.167: a. Determine re. b. Find Zi and Zo. c. Calculate Av.
> For the network of Fig. 5.166, determine Av.
> For the common-base configuration of Fig. 5.165: a. Determine re. b. Find Zi and Zo. c. Calculate Av.
> For the network of Fig. 5.164: a. Calculate IB and IC. b. Determine re. c. Determine Zi and Zo. d. Find Av.
> For the network of Fig. 5.163: a. Determine Zi and Zo. b. Find Av. c. Calculate VO if VI = 1 mV.
> For the network of Fig. 5.162: a. Determine re and bre. b. Find Zi and Zo. c. Calculate Av.
> For the network of Fig. 5.161: a. Determine re. b. Calculate VB, VCE, and VCB. c. Determine Zi and Zo. d. Calculate Av = VO>VI. e. Determine Ai = Io>Ii.
> For the network of Fig. 5.160: a. Determine re. b. Find Zi and Av.
> Using the characteristics of Fig. 4.121, design a voltage-divider configuration to have a satura- tion level of 10 mA and a Q-point one-half the distance between cutoff and saturation. The available supply is 28 V, and VE is to be one-fifth of VCC. The c
> For the network of Fig. 5.159, determine RE and RB if Av = - 10 and re = 3.8 Ω. Assume that Zb = bRE.
> Repeat Problem 19 with RE bypassed. Compare results.
> For the network of Fig. 5.158: a. Determine re. b. Find Zi and Zo. c. Calculate Av. d. Repeat parts (b) and (c) with ro = 20 kΩ
> For the network of Fig. 5.157: a. Determine re. b. Find the dc voltages VB, VCB, and VCE. c. Determine Zi and Zo. d. Calculate Av = VO>VI.
> For the network of Fig. 5.156: a. Determine re. b. Calculate VB and VC. c. Determine Zi and Av = VO>VI.
> Determine VCC for the network of Fig. 5.155 if Av = - 160 and ro = 100 kΩ.
> For the network of Fig. 5.154: a. Determine re. b. Calculate Zi and Zo. c. Find Av. d. Repeat parts (b) and (c) with ro = 25 kΩ.
> For the network of Fig. 5.153: a. Calculate IB, IC, and re. b. Determine Zi and Zo. c. Calculate Av. d. Determine the effect of ro = 30 kΩ on Av.
> For the network of Fig. 5.152, determine VCC for a voltage gain of Av = - 160.
> For the network of Fig. 5.151: a. Determine Zi and Zo. b. Find Av. c. Repeat parts (a) and (b) with ro = 20 kΩ.
> Design a voltage-divider bias network using a supply of 24 V, a transistor with a beta of 110, and an operating point of ICQ = 4 mA and VCEQ = 8 V. Choose VE = 1/2 VCC. Use standard values.
> For the common-base configuration of Fig. 5.18, the dc emitter current is 3.2 mA and a is 0.99. Determine the following if the applied voltage is 48 mV and the load is 2.2 kΩ. a. re. b. Zi. c. Ic. d. Vo. e. Av. f. Ib.
> a. What is the expected amplification of a BJT transistor amplifier if the dc supply is set to zero volts? b. What will happen to the output ac signal if the dc level is insufficient? Sketch the effect on the waveform. c. What is the conversion efficienc
> Refer to the temperature controller of Fig. 17.13. a. Sketch the waveform of the full-wave rectified waveform across the SCR. b. What is the peak current through the heater when the SCR is “on” and has a short-circuit equivalent between anode and cathode
> Refer to the charging network of Fig. 17.12. a. Determine the dc level of the full-wave rectified signal if a 1:1 transformer is employed. b. If the battery in its uncharged state is sitting at 11 V, what is the anode-to-cathode voltage drop across SCR1?
> Fully explain why reduced values of R1 in Fig. 17.11 will result in an increased angle of conduction.
> In Fig. 17.10b, why is there very little loss in potential across the SCR during conduction?
> a. Based on Fig. 17.8, will a gate current of 50 mA fire the device at room temperature (25°C)? b. Repeat part (a) for a gate current of 10 mA. c. Will a gate voltage of 2.6 V trigger the device at room temperature? d. Is VG = 6 V, IG = 800 mA a good cho
> A. At high levels of gate current, the characteristics of an SCR approach those of what two- terminal device? B. At a fixed anode-to-cathode voltage less than V(BR)F*, what is the effect on the firing of the SCR as the gate current is reduced from its ma
> a. Will the network of Example 17.3 oscillate if VBB is changed to 10 V? What minimum value of VBB is required (VV a constant)? b. Referring to the same example, what value of R would place the network in the stable “on” state and remove the oscillatory
> Can Eq. (17.24) be derived exactly as shown from Eq. (17.23)? If not, what element is missing in Eq. (17.24)?
> Design an emitter-stabilized network at ICQ / ICsat = 10 mA, = 120, and RC = 4RE. Use standard values.
> Using the data provided in Example 17.3, determine the impedance of the PUT at the firing and valley points. Are the approximate open- and short-circuit states verified?
> Determine h and VG for a put with VBB = 20 V and RB1 = 3RB2.
> a. Referring to Fig. 17.57, determine the collector current above which the switching time does not change appreciably for RL = 1 kΩ and RL = 100 Ω. b. At IC = 6 mA, how does the ratio of switching times for RL = 1 kΩ and RL = 100 Ω compare to the ratio
> a. Sketch the maximum-power curve of PD = 200 mW on the graph of Fig. 17.56. List any noteworthy conclusions. b. Determine bdc (defined by IC>IF) for the system at VCE = 15 V, IF = 10 mA. c. Compare the results of part (b) with those obtained from Fig.
> Determine from Fig. 17.55 the ratio of LED output current to detector input current for an out- put current of 20 mA. Would you consider the device to be relatively efficient in its purpose?
> a. Determine from Fig. 17.54 the average change in ICEO per degree change in temperature for the range 25°C to 50°C. b. Can the results of part (a) be used to determine the level of ICEO at 35°C? Test your theory.
> a. Determine an average derating factor from the curve of Fig. 17.58 for the region defined by temperatures between —25°C and +50°C. b. Is it fair to say that for temperatures greater than room temperature (up to 100°C), the out- put current is somewhat

