Question: Given the following data from two independent
Given the following data from two independent samples:
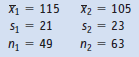
test the hypothesis of no difference between the population means against the alternative that the mean of population 1 is greater than the mean of population 2.
Transcribed Image Text:
X1 = 115 X2 = 105 S1 = 21 S2 = 23 n2 = 63 n1 49
> a. Using the data in Problem 10.3, calculate the expenditure shares on each fuel in 1999 and the individual price index number series for each fuel, with 1999 = 100. b. Use these data to construct the Laspeyres price index using the expenditures shares a
> The prices of different house types in south-east England are given in the table below: a. If the numbers of each type of house in 1991 were 1898, 1600, 1601, 499 and 1702, respectively, calculate the Laspeyres price index for 1991–94
> The following tables show energy prices and consumption in 1999–2003 (analogous to the data in the chapter for the years 2006–10). a. Construct a Laspeyres price index using 1999 as the base year. b. Construct a Paa
> The World Development Report contains data on the income distributions of many countries around the world (by quintile). Use these data to compare income distributions across countries, focusing particularly on the differences between poor countries, mid
> Compare the degrees of concentration in the following two industries. Can you say which is likely to be more competitive? Firm A В E F G H Sales 337 384 696 321 769 265 358 521 880 334 Sales 556 899 104 565 782 463 477 846 911 227
> Calculate the three-firm concentration ratio for employment in the following industry: Firm A D E F G H Employees 3350 290 440 1345 821 112 244 352 B
> For the Kravis, Heston and Summers data (Table 10.26), combine the deciles into quintiles and calculate the Gini coefficient from the quintile data. How does your answer compare with the answer given in the text, based on deciles? What do you conclude ab
> a. A government bond is issued, promising to pay the bearer £1000 in five years’ time. The prevailing market rate of interest is 7%. What price would you expect to pay now for the bond? What would its price be after two years? If, after two years, the ma
> The following data show the gross operating surplus of companies, 2005–10, in the United Kingdom, in £m. a. Turn the data into an index number series with 2005 as the reference year. b. Transform the series so that 2008 i
> a. Draw a Lorenz curve and calculate the Gini coefficient for the 1979 wealth data contained in Problem 1.5 (Chapter 1). Draw the Lorenz curve on the same diagram as you used in Problem 10.17. b. How does the answer compare to 2005 wealth data? Data fro
> Calculate the internal rates of return for the projects in Problem 10.14. Data from Problem 10.14: A firm uses a discount rate of 12% for all its investment projects. Faced with the following choice of projects, which yields the higher NPV? Projec
> A firm uses a discount rate of 12% for all its investment projects. Faced with the following choice of projects, which yields the higher NPV? Project Outlay Income stream 1 2 3 4 6 A 5600 1000 1400 1500 2100 1450 700 В 6000 800 1400 1750 2500 1925 1
> A firm is investing in a project and wishes to receive a rate of return of at least 15% on it. The stream of net income is: a. What is the present value of this income stream? b. If the investment costs £1600, should the firm invest? What
> a. If w represents the wage rate and p the price level, what is w/p? b. If ∆w represents the annual growth in wages and i is the inflation rate, what is ∆w - i? c. What does ln (w) - ln (p) represent? (ln= natural logarithm.)
> Using the data in Problem 10.6, calculate how much the average consumer would need to be compensated for the rise in prices between 1990 and 1994. Problem 10.6: The following table shows the weights in the retail price index and the values of the index
> The data below show exports and imports for the United Kingdom, 2005–10, in £bn at current prices. a. Construct index number series for exports and imports, setting the index equal to 100 in 2005 in each case. b. Is it po
> A firm has £10 000 to spend on a survey. It wishes to know the average expenditure on gas by businesses to within £30 with 99% confidence. The variance of expenditure is believed to be about 40 000. The survey costs £7000 to set up and then £15 to survey
> A firm wishes to know the average weekly expenditure on food by households to within £2, with 95% confidence. If the variance of food expenditure is thought to be about 400, what sample size does the firm need to achieve its aim?
> How would you expect the following time-series variables to look when graphed? a. The price level. b. The inflation rate. c. The £/$ exchange rate.
> Find figures for the monetary aggregate M0 for the years 1995 to 2003 in the United Kingdom, in nominal terms.
> What issues of definition arise in trying to measure ‘unemployment’?
> What issues of definition arise in trying to measure ‘output’?
> Given the following data for a family: Problem 8.2: The following data show the number of adults in each of 17 households and whether or not the family contains at least one person who smokes, to supplement the data in Problem 7.2 on alcohol spending.
> Using the results from Problem 8.1, forecast the birth rate of a country with the following characteristics: GNP equal to $3000, a growth rate of 3% p.a. and an income ratio of 7. (Construct the point estimate only). Problem 8.1: a. Using the data in P
> Build a suitable model to predict car sales in the United Kingdom. You should use time-series data (at least 20 annual observations). You should write a report in a similar manner to Problem 7.12. Data from Problem 7.12: Try to build a model of the det
> a. Calculate the rank correlation coefficient between income and quantity for the data in Problem 7.2. How does it compare to the ordinary correlation coefficient? b. Is there significant evidence that the ranks are correlated? Data from Problem 7.2: T
> Using the data from Problem 7.1, calculate the rank correlation coefficient between the variables and test its significance. How does it compare with the ordinary correlation coefficient? Data from Problem 7.1: The other data which Todaro might have us
> Predict alcohol consumption given an income of £700. Use the 99% confidence level for the interval estimate.
> The following data show the percentages of firms using computers in different aspects of their business: Is there an association between the size of firm and its use of computers? Firm size Computers used in Total numbers of firms Admin. Design Man
> How would you expect the following time-series variables to look when graphed? (e.g. Trended? Linear trend? Trended up or down? Stationary? Homoscedastic? Autocorrelated? Cyclical? Anything else?) a. Nominal national income. b. Real national income. c. T
> A survey of 100 firms found the following evidence regarding profitability and market share: Is there evidence that market share and profitability are associated? Profitability Market share <15% 15-30% >30% Low 18 7 8 Medium 11 8 High 8. 12 15 00 m
> A company wishes to see whether there are any differences between its departments in staff turnover. Looking at their records for the past year, the company finds the following data: Do the data provide evidence of a difference in staff turnover betwee
> Use the data in Table 6.3 to see if there is a significant difference between road casualties in quarters I and III on the one hand and quarters II and IV on the other. Data from Table 6.3: Table 6.3 Road casualties in Great Britain, 2014 Quarter I
> Using the data n = 70, s = 15, construct a 99% confidence interval for the true standard deviation.
> Lottery tickets are sold in different outlets: supermarkets, smaller shops and outdoor kiosks. Sales were sampled from several of each of these, with the following results: Does the evidence indicate a significant difference in sales? Use the 5% signif
> An example in Chapter 5 compared R&D expenditure in Britain and Germany. The sample data were: Is there evidence, at the 5% significance level, of difference in the variances of R&D expenditure between the two countries? What are the implicatio
> Given the following data on two sample variances, test whether there is any significant difference. Use the 1% significance level. si = 55 s3 = 48 ni 25 n2 30
> A roadside survey of the roadworthiness of vehicles obtained the following results: Is there any association between the type of vehicle and the likelihood of it being unfit for the road? Roadworthy Not roadworthy Private cars 114 30 Company cars 8
> What is the power of the test carried out in Problem 5.3? Data from Problem 5.3: A coin which is either fair or has two heads is to be tossed twice. You decide on the following decision rule: if two heads occur you will conclude it is a two-headed coin
> Using the data from Problem 1.14: Data from Problem 1.14: The table below shows the different categories of investment in the United Kingdom over a series of years: Use appropriate graphical techniques to analyse the properties of any one of the inve
> Testing the null hypothesis that μ= 10 against m > 10, a researcher obtains a sample mean of 12 with standard deviation 6 from a sample of 30 observations. Calculate the z score and the associated Prob-value for this test.
> Computer diskettes (the precursor to USB drives) which do not meet the quality required for high density diskettes are sold as low-density diskettes (storing less data) for 80 pence each. High-density diskettes are sold for £1.20 each. A firm samples 30
> In comparing two medical treatments for a disease, the null hypothesis is that the two treatments are equally effective. Why does making a Type I error not matter? What significance level for the test should be set as a result?
> a. A consumer organisation is testing two different brands of battery. A sample of 15 of brand A shows an average useful life of 410 hours with a standard deviation of 20 hours. For brand B, a sample of 20 gave an average useful life of 391 hours with st
> Two samples are drawn. The first has a mean of 150, variance 50 and sample size 12. The second has mean 130, variance 30 and sample size 15. Test the hypothesis that they are drawn from populations with the same mean.
> A photo processing company sets a quality standard of no more than 10 complaints per week on average. A random sample of 8 weeks showed an average of 13.6 complaints, with standard deviation 5.3. Is the firm achieving its quality objective?
> Consider the investor in the text, seeking out companies with weekly turnover of at least £5000. He or she applies a one-tail hypothesis test to each firm, using the 5% significance level. State whether each of the following statements is true or false (
> a. A random sample of 20 observations yielded a mean of 40 and standard deviation 10. Test the hypothesis that μ= 45 against the alternative that it is not. Use the 5% significance level. b. What assumption are you implicitly making in carrying out this
> A transport company wants to compare the fuel efficiencies of the two types of lorry it operates. It obtains data from samples of the two types of lorry, with the following results: Test the hypothesis that there is no difference in fuel efficiency, us
> Using the data from Problem 1.13: Data from Problem 1.13: The following data show car registrations in the United Kingdom for 1987–2010: a. Calculate the average rate of growth of the series. b. Calculate the standard deviation arou
> Test the hypothesis that 10% of your class or lecture group are left-handed.
> Test H0: π = 0.5 against H0: π ≠ 0.5 using p = 0.45 from a sample of size n = 35.
> From experience it is known that a certain brand of tyre lasts, on average, 15 000 miles with standard deviation 1250. A new compound is tried and a sample of 120 tyres yields an average life of 15 150 miles, with the same standard deviation. Are the new
> Given the following sample data: test the null hypothesis that the true mean is equal to 12, against a two-sided alternative hypothesis. Draw the distribution of x under the null hypothesis and indicate the rejection regions for this test. X = 15 s
> Given the sample data p = 0.4, n = 50, calculate the 99% confidence interval estimate of the true proportion.
> a. A random sample of 100 record shops found that the average weekly sale of a particular CD was 260 copies, with standard deviation of 96. Find the 95% confidence interval to estimate the true average sale for all shops. b. To compile the CD chart it is
> Given the sample data calculate the 99% confidence interval estimate of the true mean. If the sample size were 20, how would the method of calculation and width of the interval be altered? X = 40 s = 10 n = 36
> Following the previous question, prove that the most precise unbiased estimate is obtained by setting w1 = w2 = 1 2 . (Hint: Minimise V (w1x1 + w2x2) with respect to w1 after substituting w2 = 1 - w1. You will need a knowledge of calculus to solve this.
> A random sample of two observations, x1 and x2, is drawn from a population. Prove that w1x1 + w2x2 gives an unbiased estimate of the population mean as long as w1 + w2 = 1. (Hint: Prove that E (w1x1 + w2x2) = m.)
> Explain why an unbiased estimator is not always to be preferred to a biased one.
> The table below shows the different categories of investment in the United Kingdom over a series of years: Use appropriate graphical techniques to analyse the properties of any one of the investment series. Comment upon the results. (Although this seem
> Explain the difference between an estimate and an estimator. Is it true that a good estimator always leads to a good estimate?
> The heights of 10 men and 15 women were recorded, with the following results: Estimate the true difference between men’s and women’s heights. Use the 95% confidence level. Mean Variance Men 173.5 80 Women 162 65
> Two samples were drawn, each from a Normally distributed population, with the following results: Estimate the difference between the population means, using the 95% confidence level. X1 = 45 X2 = 52 S1 = 8 %3D ni = 12 $2 = 5 n2 = 18
> A sample of 12 families in a town reveals an average income of £25 000 with standard deviation £6000. Why might you be hesitant about constructing a 95% confidence interval for the average income in the town?
> A sample of 16 observations from a Normally distributed population yields a sample mean of 30 with standard deviation 5. Find the 95% confidence interval estimate of the population mean.
> Sixty-seven percent out of 150 pupils from school A passed an exam; 62% of 120 pupils at school B passed. Estimate the 99% confidence interval for the true difference between the proportions passing the exam.
> Given the sample data estimate the true difference between the means with 95% confidence. X1 = 25 X2 = 22 S2 = 18 = 100 %3D S1 = 12 ni = 80 n2
> A political opinion poll questions 1000 people. Some 464 declare they will vote Conservative. Find the 95% confidence interval estimate for the Conservative share of the vote.
> Six dice are rolled and the number of sixes is noted. Calculate the probabilities of 0, 1, . . ., 6 sixes and graph the probability distribution.
> Sketch the probability distribution for the number of accidents on the same stretch of road in one year. How and why does this differ from your previous answer?
> The following data show car registrations in the United Kingdom for 1987–2010: a. Draw a time-series graph of car registrations. Comment upon the main features of the series. (It looks daunting, but it will take you less than 10 minut
> This problem demonstrates the Central Limit Theorem at work. In your spreadsheet, use the = RAND ( ) function to generate a random sample of 25 observations (I suggest entering this function in cells A4:A28, for example). Copy these cells across 100 colu
> A coin is tossed 10 times. Write down the distribution of the number of heads, (a) exactly, using the Binomial distribution, (b) approximately, using the Normal distribution. (c) Find the probability of four or more heads, using both methods. How accurat
> If x ∼ N (10, 9), find (a). Pr (x > 12) (b). Pr (x < 7) (c). Pr (8 < x < 15) (d). Pr (x = 10)
> A multiple choice test involves 20 questions, with four choices for each answer. a. If you guessed the answers to all questions at random, what mark out of 20 would you expect to get? b. If you know the correct answer to eight of the questions, what is y
> Criticise the following statistical reasoning. The average price of a dwelling is £54 150. The average mortgage advance is £32 760. So, purchasers have to find £21 390, that is, about 40% of the purchase price. On any basis, that is an enormous outlay wh
> Demonstrate, using Σ notation, that V(kx) = k2V(x).
> Demonstrate, using Σ notation, that E (x + k) = E(x) + k.
> A four-engine plane can fly as long as at least two of its engines work. A two-engine plane flies as long as at least one engine works. The probability of an individual engine failure is 1 in 1000. a. Would you feel safer in a four- or two-engine plane,
> A firm employing 100 workers has an average absenteeism rate of 4%. On a given day, what is the probability of (a). no workers, (b). one worker, (c). more than six workers being absent?
> The UK record for the number of children born to a mother is 39, 32 of them girls. Assuming the probability of a girl in a single birth is 0.5 and that this probability is independent of previous births: (a) Find the probability of 32 girls in 39 births
> A test for AIDS is 99% successful, i.e. if you are HIV+, it will be detected in 99% of all tests, and if you are not, it will again be right 99% of the time. Assume that about 1% of the population are HIV+. You take part in a random testing procedure, wh
> A coin is either fair or has two heads. You initially assign probabilities of 0.5 to each possibility. The coin is then tossed twice, with two heads appearing. Use Bayes’ theorem to work out the posterior probabilities of each possible outcome.
> The average income of a country is known to be £10 000 with standard deviation £2500. A sample of 40 individuals is taken and their average income calculated. (a) What is the probability distribution of this sample mean? (b) What is the probability of th
> The French national lottery works as follows. Six numbers from the range 0 to 49 are chosen at random. If you have correctly guessed all six, you win the first prize. What are your chances of winning if you are allowed to choose only six numbers? A singl
> IQ (the intelligence quotient) is Normally distributed with mean 100 and standard deviation 16. (a) What proportion of the population has an IQ above 120? (b) What proportion of the population has an IQ between 90 and 110? (c) In the past, about 10% of t
> Manchester United beat Liverpool 4–2 at soccer, but you do not know the order in which the goals were scored. Draw a tree diagram to display all the possibilities and use it to find (a) the probability that the goals were scored in the order L, MU, MU, M
> Find the values of z which cut off (a) the top 10% (b) the bottom 15% (c) the middle 50% of the standard Normal distribution.
> Which of the following events are independent? a. Two flips of a fair coin. b. Two flips of a biased coin. c. Rainfall on two successive days. d. Rainfall on St. Swithin’s Day and rain one month later.
> On a test taken by 100 students, the average mark is 65, with variance 144. Student A scores 83; student B scores 47. a. Calculate the z scores for these two students. b. What is the maximum number of students with a score either better than A’s or worse
> The average income of a group of people is £8000, and 80% of the group have incomes within the range £6000–10 000. What is the minimum value of the standard deviation of the distribution?
> At another stall, you have to toss a coin numerous times. If a head does not appear in 20 tosses you win £1 billion. The entry fee for the game is £100. a. What are your expected winnings? b. Would you play?
> A newspaper advertisement reads ‘The sex of your child predicted, or your money back!’ Discuss this advertisement from the point of view of (a) the advertiser and (b) the client.
> A motorist keeps a record of petrol purchases on a long journey, as follows: Calculate the average petrol price for the journey. Petrol station 1 2 3 Litres purchased 33 40 25 Price per litre (pence) 134 139 137
> Sketch the probability distribution for the likely time of departure of a train. Locate the timetabled departure time on your chart.
> How might you estimate the probability of a corporation reneging on its bond payments?
> The data below show the number of enterprises in the United Kingdom in 2010, arranged according to employment: Number of employees Number of firms 1 ……………………………………………………………. 1 740 685 5 ……………………………………………………………. 388 990 10 ……………………………………………………………. 215
> Sketch the probability distribution for the number of accidents on a stretch of road in one day.
> A train departs every half hour. You arrive at the station at a completely random moment. Sketch the probability distribution of your waiting time. What is your expected waiting time?

