Question: The following tables show energy prices and
The following tables show energy prices and consumption in 1999–2003 (analogous to the data in the chapter for the years 2006–10).
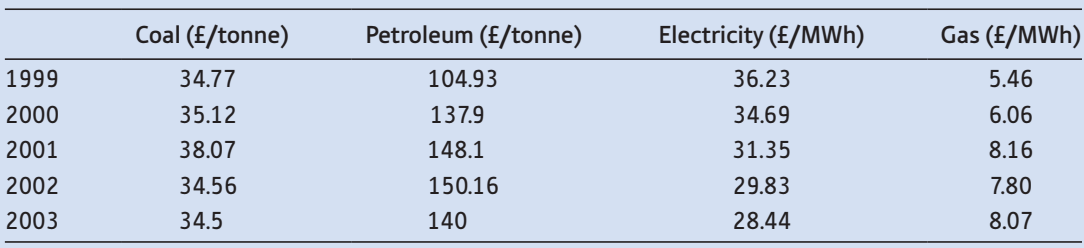
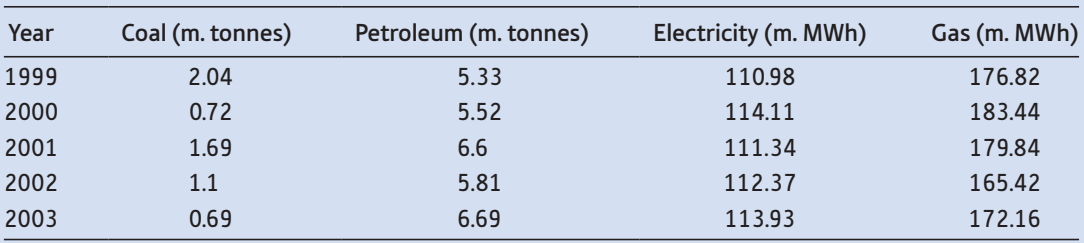
a. Construct a Laspeyres price index using 1999 as the base year.
b. Construct a Paasche price index. Compare this result with the Laspeyres index. Do they differ significantly?
c. Construct Laspeyres and Paasche quantity indices. Check that they satisfy the conditions that En = PL × QP etc.
Transcribed Image Text:
Coal (£/tonne) Petroleum (£/tonne) Electricity (£/MWh) Gas (£/MWh) 1999 34.77 104.93 36.23 5.46 2000 35.12 137.9 34.69 6.06 2001 38.07 148.1 31.35 8.16 2002 34.56 150.16 29.83 7.80 2003 34.5 140 28.44 8.07 Year Coal (m. tonnes) Petroleum (m. tonnes) Electricity (m. MWh) Gas (m. MWh) 1999 2.04 5.33 110.98 176.82 2000 0.72 5.52 114.11 183.44 2001 1.69 6.6 111.34 179.84 2002 1.1 5.81 112.37 165.42 2003 0.69 6.69 113.93 172.16
> An extremely numerate newsagent (with a spreadsheet program, as you will need) is trying to work out how many copies of a newspaper he should order. The cost to him per copy is 40 pence, which he then sells at £1.20. Sales are distributed No
> An experienced invoice clerk makes an error once in every 100 invoices, on average. (a) What is the probability of finding a batch of 100 invoices without error? (b) What is the probability of finding such a batch with more than two errors? Calculate the
> A machine producing electronic circuits has an average failure rate of 15% (they are difficult to make). The cost of making a batch of 500 circuits is £8400 and the good ones sell for £20 each. What is the probability of the firm making a loss on any one
> Two dice are thrown and the absolute difference of the two scores is recorded. Graph the resulting probability distribution and calculate its mean and variance. What is the probability that the absolute difference is 4 or more?
> Ten adults are selected at random from the population and their IQ measured. (Assume a population mean of 100 and standard deviation of 16 as in Problem 3.16.) (a) What is the probability distribution of the sample average IQ? (b) What is the probability
> Using the data from Problem 1.2: Data from Problem 1.2: The data below show the average hourly earnings (in £s) of those in full-time employment, by category of education (NVQ levels. NVQ 4 corresponds to a university degree). a. What is
> Two dice are thrown and the sum of the two scores is recorded. Draw a graph of the resulting probability distribution of the sum and calculate its mean and variance. What is the probability that the sum is 9 or greater?
> A news item revealed that a London ‘gender’ clinic (which reportedly enables you to choose the sex of your child) had just set up in business. Of its first six births, two were of the ‘wrong’ sex. Assess this from a probability point of view.
> Judy is 33, unmarried and assertive. She is a graduate in political science, and involved in union activities and anti-discrimination movements. Which of the following statements do you think is more probable? a. Judy is a bank clerk. b. Judy is a bank c
> How might you estimate the probability of Peru defaulting on its debt repayments next year? What type of probability estimate is this?
> a. Translate the following odds to ‘probabilities’: 13/8, 2/1 on, 100/30. b. In the 2.45 race at Plumpton the odds for the five runners were: Philips Woody…………………………………1/1 Gallant Effort………………………………….5/2 Satin Noir………………………………………11/2 Victory Anthem……………
> This problem is tricky, but amusing. Three gunmen, A, B and C, are shooting at each other. The probabilities that each will hit what they aim at are 1, 0.75 and 0.5, respectively. They take it in turns to shoot (in alphabetical order) and continue until
> A man is mugged and claims that the mugger had red hair. In police investigations of such cases, the victim was able correctly to identify the assailant’s hair colour 80% of the time. Assuming that 10% of the population have red hair, what is the probabi
> a. Your initial belief is that a defendant in a court case is guilty with probability 0.5. A witness comes forward claiming he saw the defendant commit the crime. You know the witness is not totally reliable and tells the truth with probability p. Use Ba
> The UK national lottery originally worked as follows. You choose six (different) numbers in the range 1 to 49. If all six come up in the draw (in any order), you win the first prize, generally valued at around £2m (which could be shared if s
> An important numerical calculation on a spacecraft is carried out independently by three computers. If all arrive at the same answer, it is deemed correct. If one disagrees, it is overruled. If there is no agreement, then a fourth computer does the calcu
> Odds’ in horserace betting are defined as follows: 3/1 (three-to-one against) means a horse is expected to win once for every three times it loses; 3/2 means two wins out of five races; 4/5 (five to four on) means five wins for every four defeats, etc. a
> Which of the following events are independent? a. A student getting the first two questions correct in a multiple-choice exam. b. A driver having an accident in successive years. c. IBM and Dell earning positive profits next year. d. Arsenal Football Clu
> Roll six sixes to win a Mercedes!’ is the announcement at a fair. You have to roll six dice. If you get six sixes you win the car, valued at £40 000. The entry ticket costs £1. What is your expected gain or loss on this game? If there are 400 people who
> The BMAT test (see http://www.ucl.ac.uk/lapt/bmat/) is an on-line test for prospective medical students. It uses ‘certainty-based marking’. After choosing your answer from the alternatives available, you then have to give your level of confidence that yo
> Criticise the following statistical reasoning. Amongst arts graduates, 10% fail to find employment. Amongst science graduates only 8% remain out of work. Therefore, science graduates are better than arts graduates. Hint: imagine there are two types of jo
> There are 25 people at a party. What is the probability that there are at least two with a birthday in common? They do not need to have been born in the same year, just the same day and month of the year. Also, ignore leap year dates. (Hint: the compleme
> A firm can build a small, medium or large factory, with anticipated profits from each dependent upon the state of demand, as in the table below. a. Which project should be chosen on the expected value criterion? b. Which project should be chosen on the
> A firm has a choice of three projects, with profits as indicated below, dependent upon the state of demand. a. Which project should be chosen on the expected value criterion? b. Which project should be chosen on the maximin and maximax criteria? c. Whi
> A bond is issued which promises to pay £400 p.a. in perpetuity. How much is the bond worth now, if the interest rate is 5%? (Hint: the sum of an infinite series of the form is 1/r, as long as r > 0.) 1 1 + 1 +r (1 + r)? (1 + r)}
> Find the anti-log of the following values: -0.09 691, 2.3, 3.3, 6.3.
> Find the anti-log of the following values: -0.823 909, 1.1, 2.1, 3.1, 12.
> Find the ln of the following values: 0.3, e, 3, 33, -1.
> Find the natural logarithms of: 0.15, 1.5, 15, 225, -4.
> Find the log of the following values: 0.8, 8, 80, 4, 16, -37.
> Find the common logarithms of: 0.15, 1.5, 15, 150, 1500, 83.7225, 9.15, -12.
> Demonstrate that Ef(x – µ)? Efx? ,2 μ Ef Ef
> Demonstrate that Ef(x – k)_ Efx Ef Ef k where k is a constant.
> Depreciation of BMW and Mercedes cars is given in the following table of new and used car prices: a. Calculate the average rate of depreciation of each type of car. b. Use the calculated depreciation rates to estimate the value of the car after 1, 2, e
> Given the following frequencies, fi associated with the x values in Problem 1A.2: {10, 6, 6, 16, 10}, evaluate: Problem 1A.2: Given the following data on xi: {8, 12, 6, 4, 10} evaluate: Efx, £fx², £f(x – 3), Efx – 3 4 Σχ, Σχ?, ( Σx;) ?, Σ (x; - 3
> Given the following frequencies, fi associated with the x values in Problem 1A.1: {5, 3, 3, 8, 5}, evaluate: Problem 1A.1: Given the following data on xi : {4, 6, 3, 2, 5} evaluate: Efx, Efx², £f(x – 3), Efx – 3 4 Ex; Ex}, ( Ex;)², > (x; – 3), Ex
> Given the following data on xi : {8, 12, 6, 4, 10} evaluate: 4 Σχ, Σχ?, ( Σx;) ?, Σ (x; - 3), Σx3. ΣΧ
> Given the following data on xi : {4, 6, 3, 2, 5} evaluate: 4 Ex; Ex}, ( Ex;)², > (x; – 3), Ex; – 3. Ex; Xi
> Evaluate: V30, V17,81/4, 15°, 12°, 3-1/3
> Evaluate: V10, V3.7,4/4,12-3, 25-3/2.
> Find the anti-ln of the following values: 3.496 508, 14, 15, -1.
> Find the anti-ln of the following values: 2.708 05, 3.708 05, 1, 10.
> A firm purchases for £30,000 a machine which is expected to last for 10 years, after which it will be sold for its scrap value of £3000. Calculate the average rate of depreciation p.a., and calculate the written-down value of the machine after one, two a
> The data below show the average hourly earnings (in £s) of those in full-time employment, by category of education (NVQ levels. NVQ 4 corresponds to a university degree). a. In what fundamental way do the data in this table differ from tho
> Using the data from Problem 1.1: Data From Problem 1.1: The following data show the education and employment status of women aged 20–29: a. Which education category has the highest proportion of women in work? What is the proportion?
> Is the 95% confidence interval (a) twice as wide, (b) more than twice as wide and (c) less than twice as wide, as the 47.5% interval? Explain your reasoning.
> a. Why is an interval estimate better than a point estimate? b. What factors determine the width of a confidence interval?
> a. Using the data in Problem 10.3, calculate the expenditure shares on each fuel in 1999 and the individual price index number series for each fuel, with 1999 = 100. b. Use these data to construct the Laspeyres price index using the expenditures shares a
> The prices of different house types in south-east England are given in the table below: a. If the numbers of each type of house in 1991 were 1898, 1600, 1601, 499 and 1702, respectively, calculate the Laspeyres price index for 1991–94
> The World Development Report contains data on the income distributions of many countries around the world (by quintile). Use these data to compare income distributions across countries, focusing particularly on the differences between poor countries, mid
> Compare the degrees of concentration in the following two industries. Can you say which is likely to be more competitive? Firm A В E F G H Sales 337 384 696 321 769 265 358 521 880 334 Sales 556 899 104 565 782 463 477 846 911 227
> Calculate the three-firm concentration ratio for employment in the following industry: Firm A D E F G H Employees 3350 290 440 1345 821 112 244 352 B
> For the Kravis, Heston and Summers data (Table 10.26), combine the deciles into quintiles and calculate the Gini coefficient from the quintile data. How does your answer compare with the answer given in the text, based on deciles? What do you conclude ab
> a. A government bond is issued, promising to pay the bearer £1000 in five years’ time. The prevailing market rate of interest is 7%. What price would you expect to pay now for the bond? What would its price be after two years? If, after two years, the ma
> The following data show the gross operating surplus of companies, 2005–10, in the United Kingdom, in £m. a. Turn the data into an index number series with 2005 as the reference year. b. Transform the series so that 2008 i
> a. Draw a Lorenz curve and calculate the Gini coefficient for the 1979 wealth data contained in Problem 1.5 (Chapter 1). Draw the Lorenz curve on the same diagram as you used in Problem 10.17. b. How does the answer compare to 2005 wealth data? Data fro
> Calculate the internal rates of return for the projects in Problem 10.14. Data from Problem 10.14: A firm uses a discount rate of 12% for all its investment projects. Faced with the following choice of projects, which yields the higher NPV? Projec
> A firm uses a discount rate of 12% for all its investment projects. Faced with the following choice of projects, which yields the higher NPV? Project Outlay Income stream 1 2 3 4 6 A 5600 1000 1400 1500 2100 1450 700 В 6000 800 1400 1750 2500 1925 1
> A firm is investing in a project and wishes to receive a rate of return of at least 15% on it. The stream of net income is: a. What is the present value of this income stream? b. If the investment costs £1600, should the firm invest? What
> a. If w represents the wage rate and p the price level, what is w/p? b. If ∆w represents the annual growth in wages and i is the inflation rate, what is ∆w - i? c. What does ln (w) - ln (p) represent? (ln= natural logarithm.)
> Using the data in Problem 10.6, calculate how much the average consumer would need to be compensated for the rise in prices between 1990 and 1994. Problem 10.6: The following table shows the weights in the retail price index and the values of the index
> The data below show exports and imports for the United Kingdom, 2005–10, in £bn at current prices. a. Construct index number series for exports and imports, setting the index equal to 100 in 2005 in each case. b. Is it po
> A firm has £10 000 to spend on a survey. It wishes to know the average expenditure on gas by businesses to within £30 with 99% confidence. The variance of expenditure is believed to be about 40 000. The survey costs £7000 to set up and then £15 to survey
> A firm wishes to know the average weekly expenditure on food by households to within £2, with 95% confidence. If the variance of food expenditure is thought to be about 400, what sample size does the firm need to achieve its aim?
> How would you expect the following time-series variables to look when graphed? a. The price level. b. The inflation rate. c. The £/$ exchange rate.
> Find figures for the monetary aggregate M0 for the years 1995 to 2003 in the United Kingdom, in nominal terms.
> What issues of definition arise in trying to measure ‘unemployment’?
> What issues of definition arise in trying to measure ‘output’?
> Given the following data for a family: Problem 8.2: The following data show the number of adults in each of 17 households and whether or not the family contains at least one person who smokes, to supplement the data in Problem 7.2 on alcohol spending.
> Using the results from Problem 8.1, forecast the birth rate of a country with the following characteristics: GNP equal to $3000, a growth rate of 3% p.a. and an income ratio of 7. (Construct the point estimate only). Problem 8.1: a. Using the data in P
> Build a suitable model to predict car sales in the United Kingdom. You should use time-series data (at least 20 annual observations). You should write a report in a similar manner to Problem 7.12. Data from Problem 7.12: Try to build a model of the det
> a. Calculate the rank correlation coefficient between income and quantity for the data in Problem 7.2. How does it compare to the ordinary correlation coefficient? b. Is there significant evidence that the ranks are correlated? Data from Problem 7.2: T
> Using the data from Problem 7.1, calculate the rank correlation coefficient between the variables and test its significance. How does it compare with the ordinary correlation coefficient? Data from Problem 7.1: The other data which Todaro might have us
> Predict alcohol consumption given an income of £700. Use the 99% confidence level for the interval estimate.
> The following data show the percentages of firms using computers in different aspects of their business: Is there an association between the size of firm and its use of computers? Firm size Computers used in Total numbers of firms Admin. Design Man
> How would you expect the following time-series variables to look when graphed? (e.g. Trended? Linear trend? Trended up or down? Stationary? Homoscedastic? Autocorrelated? Cyclical? Anything else?) a. Nominal national income. b. Real national income. c. T
> A survey of 100 firms found the following evidence regarding profitability and market share: Is there evidence that market share and profitability are associated? Profitability Market share <15% 15-30% >30% Low 18 7 8 Medium 11 8 High 8. 12 15 00 m
> A company wishes to see whether there are any differences between its departments in staff turnover. Looking at their records for the past year, the company finds the following data: Do the data provide evidence of a difference in staff turnover betwee
> Use the data in Table 6.3 to see if there is a significant difference between road casualties in quarters I and III on the one hand and quarters II and IV on the other. Data from Table 6.3: Table 6.3 Road casualties in Great Britain, 2014 Quarter I
> Using the data n = 70, s = 15, construct a 99% confidence interval for the true standard deviation.
> Lottery tickets are sold in different outlets: supermarkets, smaller shops and outdoor kiosks. Sales were sampled from several of each of these, with the following results: Does the evidence indicate a significant difference in sales? Use the 5% signif
> An example in Chapter 5 compared R&D expenditure in Britain and Germany. The sample data were: Is there evidence, at the 5% significance level, of difference in the variances of R&D expenditure between the two countries? What are the implicatio
> Given the following data on two sample variances, test whether there is any significant difference. Use the 1% significance level. si = 55 s3 = 48 ni 25 n2 30
> A roadside survey of the roadworthiness of vehicles obtained the following results: Is there any association between the type of vehicle and the likelihood of it being unfit for the road? Roadworthy Not roadworthy Private cars 114 30 Company cars 8
> What is the power of the test carried out in Problem 5.3? Data from Problem 5.3: A coin which is either fair or has two heads is to be tossed twice. You decide on the following decision rule: if two heads occur you will conclude it is a two-headed coin
> Using the data from Problem 1.14: Data from Problem 1.14: The table below shows the different categories of investment in the United Kingdom over a series of years: Use appropriate graphical techniques to analyse the properties of any one of the inve
> Testing the null hypothesis that μ= 10 against m > 10, a researcher obtains a sample mean of 12 with standard deviation 6 from a sample of 30 observations. Calculate the z score and the associated Prob-value for this test.
> Computer diskettes (the precursor to USB drives) which do not meet the quality required for high density diskettes are sold as low-density diskettes (storing less data) for 80 pence each. High-density diskettes are sold for £1.20 each. A firm samples 30
> In comparing two medical treatments for a disease, the null hypothesis is that the two treatments are equally effective. Why does making a Type I error not matter? What significance level for the test should be set as a result?
> a. A consumer organisation is testing two different brands of battery. A sample of 15 of brand A shows an average useful life of 410 hours with a standard deviation of 20 hours. For brand B, a sample of 20 gave an average useful life of 391 hours with st
> Two samples are drawn. The first has a mean of 150, variance 50 and sample size 12. The second has mean 130, variance 30 and sample size 15. Test the hypothesis that they are drawn from populations with the same mean.
> A photo processing company sets a quality standard of no more than 10 complaints per week on average. A random sample of 8 weeks showed an average of 13.6 complaints, with standard deviation 5.3. Is the firm achieving its quality objective?
> Consider the investor in the text, seeking out companies with weekly turnover of at least £5000. He or she applies a one-tail hypothesis test to each firm, using the 5% significance level. State whether each of the following statements is true or false (
> a. A random sample of 20 observations yielded a mean of 40 and standard deviation 10. Test the hypothesis that μ= 45 against the alternative that it is not. Use the 5% significance level. b. What assumption are you implicitly making in carrying out this
> A transport company wants to compare the fuel efficiencies of the two types of lorry it operates. It obtains data from samples of the two types of lorry, with the following results: Test the hypothesis that there is no difference in fuel efficiency, us
> Given the following data from two independent samples: test the hypothesis of no difference between the population means against the alternative that the mean of population 1 is greater than the mean of population 2. X1 = 115 X2 = 105 S1 = 21 S2 =
> Using the data from Problem 1.13: Data from Problem 1.13: The following data show car registrations in the United Kingdom for 1987–2010: a. Calculate the average rate of growth of the series. b. Calculate the standard deviation arou
> Test the hypothesis that 10% of your class or lecture group are left-handed.
> Test H0: π = 0.5 against H0: π ≠ 0.5 using p = 0.45 from a sample of size n = 35.
> From experience it is known that a certain brand of tyre lasts, on average, 15 000 miles with standard deviation 1250. A new compound is tried and a sample of 120 tyres yields an average life of 15 150 miles, with the same standard deviation. Are the new

