Question: Graph the given functions on the same
Graph the given functions on the same screen. How are these graphs related?
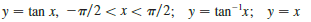
Transcribed Image Text:
y = tan x, - 7/2 < x < m/2; y= tan='x; y = x
> Differentiate the function. y = ln (e-x + xe-x)
> Differentiate the function. y = ln |2 – x = 5x2|
> Differentiate the function. F (y) = y ln (1 + ey)
> Prove that cos (sin-1 x) = √1 – x2.
> Find the exact value of each expression. cos (tan-1 2 + tan-13)
> Find the exact value of each expression. sin (2 tan-1 √2)
> (a). Evaluate limx→∞ x sin 1/x. (b). Evaluate limx→0 x sin 1/x. (c). Illustrate parts (a) and (b) by graphing y = x sin (1/x).
> Find the exact value of each expression. csc (arccsc3/5)
> Find the exact value of each expression. tan (sin-1 (2/3)
> A semicircle with diameter PQ sits on an isosceles triangle PQR to form a region shaped like a two-dimensional ice-cream cone, as shown in the figure. If A (θ) is the area of the semicircle and B (θ)is the area of the triangle,
> (a). The van der Waals equation for n moles of a gas is where P is the pressure V, is the volume, and T is the temperature of the gas. The constant R is the universal gas constant and a and b are positive constants that are characteristic of a particular
> Find the value of the number a such that the families of curves y = (x + c)-1 and y = a (x + k)1/3 are orthogonal trajectories.
> Show that the ellipse x2/a2+ y2/b2 = 1 and the hyperbola x2/A2 – y2/B2 = 1 are orthogonal trajectories if A2 < a2 and a2 – b2 = A2 + B2 (so the ellipse and hyperbola have the same foci).
> (a). Sketch the graph of the function f (x) = sin (sin-1 x). (b). Sketch the graph of the function g (x) = sin-1 (sin x), x ∈ R (c). Show that g'(x) = cos x/|cos x|. (d). Sketch the graph of h (x) = cos-1 (sin x), x ∈ R, and find its derivative.
> Use the formula from Exercise 41(a) to prove Exercise 41(a): (a). Suppose f is a one-to-one differentiable function and its inverse function f-1 is also differentiable. Use implicit differentiation to show that (f-1)'(x) = 1/f'(f-1(x)) provided that th
> (a). Show that f (x) = 2x + cos x is one-to-one. (b). What is the value of f-1(1)? (c). Use the formula from Exercise 41(a) to find (f-1)'(1). Exercise 41(a): (a). Suppose f is a one-to-one differentiable function and its inverse function f-1 is also d
> (a). Suppose f is a one-to-one differentiable function and its inverse function f-1 is also differentiable. Use implicit differentiation to show that (f-1)'(x) = 1/f'(f-1(x)) provided that the denominator is not 0. (b). If f (4) = 5 and f'(4) = 2/3, find
> If f and g are the functions whose graphs are shown, let u (x) = f (x) g (x) and v (x) = f (x) /g (x). (a). Find u'(1) (b). Find v'(5)
> Find the limit. limx→0+ tan-1 (ln x)
> Find the exact value of each expression. (a). tan-1 (tan3π/4) (b). cos (arccos ½)
> Find the limit. limx→∞+ arctan (ex)
> Find the limit. limx→∞ arccos (1 + x2/1 + 2x2)
> Find the limit. Limx→-1+ sin-1 x
> Find f'(x). Check that your answer is reasonable by comparing the graphs of f and f'. f (x) = arctan (x2 -x)
> Find f'(x). Check that your answer is reasonable by comparing the graphs of f and f'. f (x) = √1 - x2 arcsin x
> Find an equation of the tangent line to the curve y = 3 arccos (x/2) at the point (1, π).
> If g (x) = x sin (x/4) + √16 – x2, find g'(2).
> Find y' if tan-1 (xy) = 1 + x2y.
> The figure shows the graphs of four functions. One is the position function of a car, one is the velocity of the car, one is its acceleration, and one is its jerk. Identify each curve, and explain your choices. у. a b
> Find the derivative of the function. Find the domains of the function and its derivative. g (x) = c0s-1 (3 – 2x)
> Find the derivative of the function. Find the domains of the function and its derivative. f (x) = arcsin (ex)
> Find the exact value of each expression. (a). arctan 1 (b). sin-1 (1/√2)
> Find the derivative of the function. Simplify where possible. y = arccos (b + a cos x/a + b cos x), 0 < x < π, a > b > 0
> Find the derivative of the function. Simplify where possible. y = arctan √1-x/1+x
> Find the derivative of the function. Simplify where possible. y = x sin-1 x + √1 – x2
> Find the derivative of the function. Simplify where possible. y = cos-1 (sin-1 t)
> Find the derivative of the function. Simplify where possible. y = arctan (cos θ)
> Find the derivative of the function. Simplify where possible. y = tan-1 (x – √1 + x2)
> Find the derivative of the function. Simplify where possible. y = cos-1(e2x)
> The figure shows the graphs of three functions. One is the position function of a car, one is the velocity of the car, and one is its acceleration. Identify each curve, and explain your choices. y b
> Find the derivative of the function. Simplify where possible. f (x) = x ln (arctan x)
> Find the derivative of the function. Simplify where possible. G (x) = √1 – x2 arccos x
> Find the derivative of the function. Simplify where possible. F (θ) = arcsin √sin θ
> Find the exact value of each expression. (a). tan-1 (1/√3) (b). sec-1 (2)
> Find the derivative of the function. Simplify where possible. y = sin-1 (2x + 1)
> Find the derivative of the function. Simplify where possible. y = tan-1 (x2)
> Find the derivative of the function. Simplify where possible. y = (tan-1 x)2
> (a). Prove that sin-1 x = π/2. (b). Use part (a) to prove Formula 2. sin1x cos1x
> Prove Formula 2 by the same method as for Formula 1.
> The figure shows graphs of f, f', f'' and f'''. Identify each curve, and explain your choices. a b c d
> Graph the given functions on the same screen. How are these graphs related? y = sin x, -7/2 sIS /2; y= sin-'x; y = x
> Simplify the expression. cos (2 tan-1 x)
> Simplify the expression. sin (tan-1 x)
> Simplify the expression. tan (sin-1 x)
> Find the exact value of each expression. (a). sin-1 (√3/2) (b). cos-1 (-1)
> Find dy/dx by implicit differentiation. x2y2 + x sin y = 4
> Find dy/dx by implicit differentiation. y5 + x2y3 = 1+ yex2
> Find dy/dx by implicit differentiation. x4 (x + y) = y2 (3x – y)
> Find dy/dx by implicit differentiation. 2x3 + x2y – xy3 = 2
> Find dy/dx by implicit differentiation. x2 + xy – y2 = 4
> Two curves are orthogonal if their tangent lines are perpendicular at each point of intersection. Show that the given families of curves are orthogonal trajectories of each other, that is, every curve in one family is orthogonal to every curve in the oth
> Two curves are orthogonal if their tangent lines are perpendicular at each point of intersection. Show that the given families of curves are orthogonal trajectories of each other, that is, every curve in one family is orthogonal to every curve in the oth
> Two curves are orthogonal if their tangent lines are perpendicular at each point of intersection. Show that the given families of curves are orthogonal trajectories of each other, that is, every curve in one family is orthogonal to every curve in the oth
> Two curves are orthogonal if their tangent lines are perpendicular at each point of intersection. Show that the given families of curves are orthogonal trajectories of each other, that is, every curve in one family is orthogonal to every curve in the oth
> Find an equation of the tangent line to the curve at the given point. y = (1 + 2x)10, (0, 1)
> Show by implicit differentiation that the tangent to the ellipse x2/a2 + y2/b2 = 1 at the point (x0, y0) is x0x/a2 + y0y/b2 = 1
> Find dy/dx by implicit differentiation. 2√x + √y = 3
> Find y' and y". y = eax sin βx
> Find y' and y". y = cos2x
> Find y' and y". y = cos (x2)
> Find the derivative of the function. y = 23x2
> Zoom in toward the points (1, 0), (0, 1), and (-1, 0) on the graph of the function g (x) = (x2 – 1)2/3. What do you notice? Account for what you see in terms of the differentiability of g.
> A particle moves according to a law of motion s = f (t), t > 0, where is measured in seconds and in feet. (a). Find the velocity at time t. (b). What is the velocity after 3 s? (c). When is the particle at rest? (d). When is the particle moving in the po
> Find the derivative of the function. y = cos √sin (tan πx)
> Find y" by implicit differentiation. x4 + y4 = a4
> Find y" by implicit differentiation. x3 + y3 = 1
> Find y" by implicit differentiation. √x + √y = 1
> Find y" by implicit differentiation. 9x2 + y2 = 9
> Find the derivative of the function. f (t) = √t/t2 + 4
> Find dy/dx by implicit differentiation. x3 + y3 = 1
> (a). The curve with equation y2 = 5x4 – x2 is called a kampyle of Eudoxus. Find an equation of the tangent line to this curve at the point (1, 2). (b). Illustrate part (a) by graphing the curve and the tangent line on a common screen. (If your graphing d
> Use implicit differentiation to find an equation of the tangent line to the curve at the given point. у? - 4) — х"({? - 5) К0, —2) (devil's curve) y
> Use implicit differentiation to find an equation of the tangent line to the curve at the given point. 2(x? + y?)? = 25(x² – y²) (3, 1) (lemniscate) y4
> Find the points on the lemniscate in Exercise 27 where the tangent is horizontal. Exercise 27: Use implicit differentiation to find an equation of the tangent line to the curve at the given point. 2(x? + y?)? = 25(x² – y²) (3, 1) (lemniscate) y4
> Use implicit differentiation to find an equation of the tangent line to the curve at the given point. x2/3 + y2/3 = 4 (-3 √3, 1) (astroid) 8
> Use implicit differentiation to find an equation of the tangent line to the curve at the given point. x2 + y2 = (2x2 + 2y2) – x)2 (0, 1 /2) (cardioid) y.
> Use implicit differentiation to find an equation of the tangent line to the curve at the given point. x² + 2xy – y² + x = 2, (1, 2) (hyperbola)
> Use implicit differentiation to find an equation of the tangent line to the curve at the given point. x² + xy + y? = 3, (1, 1) (ellipse)
> Use implicit differentiation to find an equation of the tangent line to the curve at the given point. sin(x + y) = 2x – 2y, (7, 7) %3D
> Use implicit differentiation to find an equation of the tangent line to the curve at the given point. y sin 2x = x cos 2y, (7/2, 7/4)
> Regard as the independent variable and as the dependent variable and use implicit differentiation to find dx/dy. y sec x = x tan y
> Write the composite function in the form f (g (x)). [Identify the inner function u = g (x) and the outer function y = f (u).] Then find the derivative dy/dx. y = (2x3 + 5)4
> Regard as the independent variable and as the dependent variable and use implicit differentiation to find dx/dy. x4y2 - x3y + 2xy3 = 0
> If g (x) + x sin g (x) = x2, find g'(0).
> (a). The curve with equation has been likened to a bouncing wagon. Use a computer algebra system to graph this curve and discover why. (b). At how many points does this curve have horizontal tangent lines? Find the x-coordinates of these points.
> If f (x) + x2 [f (x)]3 = 10 and f (1) = 2, find f'(1).
> Find dy/dx by implicit differentiation. sin x + cos y = sin x cos y
> Find dy/dx by implicit differentiation. ey cos x = 1 + sin (xy)
> Find dy/dx by implicit differentiation. tan (x – y) = y/1 + xy2
> Find dy/dx by implicit differentiation. ex/y = x - y

