Question: If a matrix is in reduced form,
If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
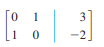
> Repeat Problem 95 if 650 telephone contacts and 350 house contacts are needed. Data from problem95: Two sociologists have grant money to study school busing in a particular city. They wish to conduct an opinion survey using 600 telephone contacts and 40
> Refer to Problem 92. Subsequent data indicated that life expectancy grew to 73.2 years for males born during 1995–2000 and to 74.3 years for males born during 2000–2005. Add the points (15, 73.2) and (20, 74.3) to the data set in Problem 92. Use a graphi
> The life expectancy for males born during 1980–1985 was approximately 70.7 years. This grew to 71.1 years during 1985–1990 and to 71.8 years during 1990–1995. Construct a model for this data by finding a quadratic equation whose graph passes through the
> A real estate company with 14 employees in its central office, 8 in its north office, and 6 in its south office is planning to lay off 12 employees. (A) How many ways can this be done? (B) The company decides to lay off 5 employees from the central off
> The population of California was approximately 30 million in 1990, 34 million in 2000, and 37 million in 2010. Construct a model for this data by finding a quadratic equation whose graph passes through the points (0, 30), (10, 34), and (20, 37). Use this
> Refer to Problem 86. The costs of the four brands are Brand A, $1.50; Brand B, $3.00; Brand C, $3.75; and Brand D, $2.25. Which of the solutions to Problem 86 would minimize the cost of the rat food? Data from problem 86: In a laboratory experiment, rat
> In a laboratory experiment, rats are to be fed 5 packets of food containing a total of 80 units of vitamin E. There are four different brands of food packets that can be used. A packet of brand A contains 5 units of vitamin E, a packet of brand B contain
> Repeat Problem 83 if the diet is to include exactly 400 units of calcium, 160 units of iron, and 240 units of vitamin A. Data from problem83: A dietitian in a hospital is to arrange a special diet composed of three basic foods. The diet is to include ex
> Repeat Problem 81 if tax law is changed so that the taxable income of a company is defined to be all of its own annual net income plus its share of the taxable income of each of the other companies. Data from problem 81: As a result of several mergers a
> Repeat Problem 79 if local taxes are not allowed as a deduction for federal and state taxes. Data from problem79: A corporation has a taxable income of $7,650,000. At this income level, the federal income tax rate is 50%, the state tax rate is 20%, and
> Refer to Problem 76. The cost of leasing a 10-passenger airplane is $8,000 per month, a 15-passenger airplane is $14,000 per month, and a 20-passenger airplane is $16,000 per month. Which of the solutions to Problem 76 would minimize the monthly leasing
> A corporation wants to lease a fleet of 12 airplanes with a combined carrying capacity of 220 passengers. The three available types of planes carry 10, 15, and 20 passengers, respectively. How many of each type of plane should be leased?
> Repeat Problem 73 assuming that the cutting, assembly, and packaging departments have available a maximum of 350, 330, and 115 labor-hours per week, respectively. Data from 73: A small manufacturing plant makes three types of inflatable boats: one-perso
> Find a, b, and c so that the graph of the quadratic equation y = ax2 + bx + c passes through the points 1 -1, -52, 12, 72, and 15, 12.
> An electronics store receives a shipment of 30 graphing calculators, including 6 that are defective. Four of these calculators are selected for a local high school. (A) How many selections can be made? (B) How many of these selections will contain no d
> Solve Problems using Gauss–Jordan elimination.
> Solve Problems using Gauss–Jordan elimination
> Solve Problems using Gauss–Jordan elimination.
> Consider a system of three linear equations in three variables. Give examples of two reduced forms that are not row-equivalent if the system is (A) Consistent and dependent (B) Inconsistent
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Note from the table in the graphing calculator display that the largest value of nCr when n = 21 is 21C10 = 21C11 = 352,716. Use a similar table to find the largest value of nCr when n = 17.
> Evaluate the expression. If the answer is not an integer, round to four decimal places.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Use row operations to change each matrix to reduced form.
> Use row operations to change each matrix to reduced form.
> Use row operations to change each matrix to reduced form.
> Use row operations to change each matrix to reduced form.
> Discuss the validity of each statement about linear systems. If the statement is always true, explain why. If not, give a counterexample. If there are no all-zero rows, then the system has exactly one solution.
> Discuss the validity of each statement about linear systems. If the statement is always true, explain why. If not, give a counterexample. If the number of leftmost ones is less than the number of variables and the system is consistent, then the system h
> Discuss the validity of each statement about linear systems. If the statement is always true, explain why. If not, give a counterexample. If the number of leftmost ones is less than the number of variables, then the system has infinitely many solutions
> In which of Problems 20, 22, 24, 26, and 28 is the number of leftmost ones less than the number of variables?
> Let U be the set of all 2-card hands, let K be the set of all 2-card hands that contain exactly 1 king, and let Q be the set of all 2-card hands that contain exactly 1 queen. Find n(K ∩ Q′), n(K ∩ Q), n(K′ ∩ Q), and n(K′ ∩ Q′).
> In which of Problems 20, 22, 24, 26, and 28 is the number of leftmost ones equal to the number of variables?
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
> If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
> If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
> If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
> How many 4-person committees are possible from a group of 9 people if (A) There are no restrictions? (B) Both Jim and Mary must be on the committee? (C) Either Jim or Mary (but not both) must be on the committee?
> Refer to the following matrices: List the elements on the principal diagonal of B.
> Refer to the following matrices: Which of the matrices does not contain the element 0?
> Refer to the following matrices: Which of the matrices is a row matrix?
> Refer to the following matrices: What is the size of A? Of C?
> Refer to the following matrices: How many elements are there in B? In D?
> Solve by using augmented matrix methods. Use a graphing calculator to perform the row operations.
> Solve by using augmented matrix methods. Use a graphing calculator to perform the row operations.
> Solve by Using augmented matrix methods.
> Solve by Using augmented matrix methods.
> In how many ways can 3 people sit in a row of 7 chairs?
> Solve by Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Five distinct points are selected on the circumference of a circle. (A) How many line segments can be drawn by joining the points in all possible ways? (B) How many triangles can be drawn using these 5 points as vertices? (C) How many quadrilaterals c
> Using augmented matrix methods.
> Each of the matrices in below Problems is the final matrix form for a system of two linear equations in the variables x1 and x2. Write the solution of the system.
> Each of the matrices in below Problems is the final matrix form for a system of two linear equations in the variables x1 and x2. Write the solution of the system.
> Each of the matrices in below Problem is the final matrix form for a system of two linear equations in the variables x1 and x2. Write the solution of the system. Answer: x1 ( 3 , x2 ( (5
> Using augmented matrix methods. Write the linear system represented by each augmented matrix in your solution, and solve each of these systems graphically. Discuss the relationships among the solutions of these systems.
> Using augmented matrix methods. Graph each solution set. Discuss the differences between the graph of an equation in the system and the graph of the system’s solution set.
> Using augmented matrix methods. Graph each solution set. Discuss the differences between the graph of an equation in the system and the graph of the system’s solution set.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Discuss the validity of each statement. If the statement is true, explain why. If not, give a counter example. If n and r are positive integers and 1 < r < n, then nPr = nPn - r.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix. Answer:
> Write the system of linear equations that is represented by the given augmented matrix. Assume that the variables are x1 and x2.
> Write the system of linear equations that is represented by the given augmented matrix. Assume that the variables are x1 and x2.
> Write the coefficient matrix and the augmented matrix of the given system of linear equations.
> Discuss the validity of each statement. If the statement is true, explain why. If not, give a counter example. If n and r are positive integers and 1 < r < n, then nCr < nCr + 1.
> Write the coefficient matrix and the augmented matrix of the given system of linear equations.
> Refer to the following matrices: For matrix D, find d11 + d21
> Refer to the following matrices: For matrix A, list the elements a21, a12.
> Find an equation in point–slope form, y - y1 = m(x - x1), of the line through the given points. (3, 20) and 1 -5, 42.
> Find the x and y coordinates of the intersection of the given lines. 6x - 5y = 120 and y = 3
> Find the x and y coordinates of the intersection of the given lines. 3x + 4y = 72 and the y axis
> Find the x and y coordinates of the intersection of the given lines. y = 5x + 7 and the x axis
> A ship using sound-sensing devices above and below water recorded a surface explosion 6 seconds sooner by its underwater device than its above-water device. Sound travels in air at 1,100 feet per second and in seawater at 5,000 feet per second. How long

