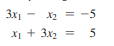Question: Using augmented matrix methods. /
> Solve Problems using Gauss–Jordan elimination.
> Consider a system of three linear equations in three variables. Give examples of two reduced forms that are not row-equivalent if the system is (A) Consistent and dependent (B) Inconsistent
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Note from the table in the graphing calculator display that the largest value of nCr when n = 21 is 21C10 = 21C11 = 352,716. Use a similar table to find the largest value of nCr when n = 17.
> Evaluate the expression. If the answer is not an integer, round to four decimal places.
> Solve by using Gauss–Jordan elimination.
> Solve by using Gauss–Jordan elimination.
> Use row operations to change each matrix to reduced form.
> Use row operations to change each matrix to reduced form.
> Use row operations to change each matrix to reduced form.
> Use row operations to change each matrix to reduced form.
> Discuss the validity of each statement about linear systems. If the statement is always true, explain why. If not, give a counterexample. If there are no all-zero rows, then the system has exactly one solution.
> Discuss the validity of each statement about linear systems. If the statement is always true, explain why. If not, give a counterexample. If the number of leftmost ones is less than the number of variables and the system is consistent, then the system h
> Discuss the validity of each statement about linear systems. If the statement is always true, explain why. If not, give a counterexample. If the number of leftmost ones is less than the number of variables, then the system has infinitely many solutions
> In which of Problems 20, 22, 24, 26, and 28 is the number of leftmost ones less than the number of variables?
> Let U be the set of all 2-card hands, let K be the set of all 2-card hands that contain exactly 1 king, and let Q be the set of all 2-card hands that contain exactly 1 queen. Find n(K ∩ Q′), n(K ∩ Q), n(K′ ∩ Q), and n(K′ ∩ Q′).
> In which of Problems 20, 22, 24, 26, and 28 is the number of leftmost ones equal to the number of variables?
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> Write the solution of the linear system corresponding to each reduced augmented matrix.
> If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
> If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
> If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
> If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
> How many 4-person committees are possible from a group of 9 people if (A) There are no restrictions? (B) Both Jim and Mary must be on the committee? (C) Either Jim or Mary (but not both) must be on the committee?
> If a matrix is in reduced form, say so. If not, explain why and indicate a row operation that completes the next step of Gauss–Jordan elimination.
> Refer to the following matrices: List the elements on the principal diagonal of B.
> Refer to the following matrices: Which of the matrices does not contain the element 0?
> Refer to the following matrices: Which of the matrices is a row matrix?
> Refer to the following matrices: What is the size of A? Of C?
> Refer to the following matrices: How many elements are there in B? In D?
> Solve by using augmented matrix methods. Use a graphing calculator to perform the row operations.
> Solve by using augmented matrix methods. Use a graphing calculator to perform the row operations.
> Solve by Using augmented matrix methods.
> Solve by Using augmented matrix methods.
> In how many ways can 3 people sit in a row of 7 chairs?
> Solve by Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Five distinct points are selected on the circumference of a circle. (A) How many line segments can be drawn by joining the points in all possible ways? (B) How many triangles can be drawn using these 5 points as vertices? (C) How many quadrilaterals c
> Using augmented matrix methods.
> Each of the matrices in below Problems is the final matrix form for a system of two linear equations in the variables x1 and x2. Write the solution of the system.
> Each of the matrices in below Problems is the final matrix form for a system of two linear equations in the variables x1 and x2. Write the solution of the system.
> Each of the matrices in below Problem is the final matrix form for a system of two linear equations in the variables x1 and x2. Write the solution of the system. Answer: x1 ( 3 , x2 ( (5
> Using augmented matrix methods. Write the linear system represented by each augmented matrix in your solution, and solve each of these systems graphically. Discuss the relationships among the solutions of these systems.
> Using augmented matrix methods. Graph each solution set. Discuss the differences between the graph of an equation in the system and the graph of the system’s solution set.
> Using augmented matrix methods. Graph each solution set. Discuss the differences between the graph of an equation in the system and the graph of the system’s solution set.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Discuss the validity of each statement. If the statement is true, explain why. If not, give a counter example. If n and r are positive integers and 1 < r < n, then nPr = nPn - r.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix. Answer:
> Write the system of linear equations that is represented by the given augmented matrix. Assume that the variables are x1 and x2.
> Write the system of linear equations that is represented by the given augmented matrix. Assume that the variables are x1 and x2.
> Write the coefficient matrix and the augmented matrix of the given system of linear equations.
> Discuss the validity of each statement. If the statement is true, explain why. If not, give a counter example. If n and r are positive integers and 1 < r < n, then nCr < nCr + 1.
> Write the coefficient matrix and the augmented matrix of the given system of linear equations.
> Refer to the following matrices: For matrix D, find d11 + d21
> Refer to the following matrices: For matrix A, list the elements a21, a12.
> Find an equation in point–slope form, y - y1 = m(x - x1), of the line through the given points. (3, 20) and 1 -5, 42.
> Find the x and y coordinates of the intersection of the given lines. 6x - 5y = 120 and y = 3
> Find the x and y coordinates of the intersection of the given lines. 3x + 4y = 72 and the y axis
> Find the x and y coordinates of the intersection of the given lines. y = 5x + 7 and the x axis
> A ship using sound-sensing devices above and below water recorded a surface explosion 6 seconds sooner by its underwater device than its above-water device. Sound travels in air at 1,100 feet per second and in seawater at 5,000 feet per second. How long
> Repeat Problem 81 if the object is 240 feet above the ground after 1 second and 192 feet above the ground after 2 seconds. Data from 81: An object dropped off the top of a tall building falls vertically with constant acceleration. If s is the distance o
> A company produces Italian sausages and bratwursts at plants in Green Bay and Sheboygan. The hourly production rates at each plant are given in the table. How many hours should each plant operate to exactly fill an order for 62,250 Italian sausages and 7
> Discuss the validity of each statement. If the statement is true, explain why. If not, give a counter example. If n is a positive integer greater than 3, then n! > 2n.
> A fruit grower uses two types of fertilizer in an orange grove, brand A and brand B. Each bag of brand A contains 8 pounds of nitrogen and 4 pounds of phosphoric acid. Each bag of brand B contains 7 pounds of nitrogen and 6 pounds of phosphoric acid. Tes
> Refer to Problem 75. (A) If the company decides to discontinue production of the robust blend and produce only the mild blend, how many pounds of the mild blend can the company produce? How many beans of each type will the company use? Are there any bea
> Refer to Problem 73. Federated Shipping, a competing overnight delivery service, informs the customer in Problem 73 that they would ship the 5-pound package for $29.95 and the 20-pound package for $59.20. (A) If Federated Shipping computes its cost in t
> Repeat Problem 71 if the monthly fixed costs increase to $27,200, the variable costs increase to $9.15, and the company raises the selling price of the DVDs to $21.95 Data from 71: A company markets exercise DVDs that sell for $19.95, including shipping
> Repeat Problem 69 with the cost and revenue equations Data from problem 69: A small plant manufactures riding lawn mowers. The plant has fixed costs (leases, insurance, etc.) of $48,000 per day and variable costs (labor, materials, etc.) of $1,400 per u
> At $2.13 per bushel, the annual supply for corn in the Midwest is 8.9 billion bushels and the annual demand is 6.5 billion bushels. When the price falls to $1.50 per bushel, the annual supply decreases to 8.2 billion bushels and the annual demand increas
> Suppose that the supply and demand for printed baseball caps for a particular week are / where p is the price in dollars and q is the quantity in hundreds. (A) Find the supply and demand (to the nearest unit) if baseball caps are $4 each. Discuss the s
> Repeat Problem 63 for the following systems: (A) 6x - 5y = 10 -13x + 11y = -20 (B) 6x - 5y = 10 -13x + 10y = -20 (C) 6x - 5y = 10 -12x + 10y = -20 Data from Problem 63: The coefficients of the three systems given below are similar. One might gue
> Graph the equations in the same coordinate system. Find the coordinates of any points where two or more lines intersect. Is there a point that is a solution to all three equations?
> Graph the equations in the same coordinate system. Find the coordinates of any points where two or more lines intersect. Is there a point that is a solution to all three equations?
> Refer to the table in the graphing calculator display below, which shows y1 = nPr and y2 = nCr for n = 6. Explain how the table illustrates the formula nPr = r!nCr
> Graph the equations in the same coordinate system. Find the coordinates of any points where two or more lines intersect. Is there a point that is a solution to all three equations?
> Use a graphing calculator to find the solution to each system. Round any approximate solutions to three decimal places.
> Use a graphing calculator to find the solution to each system. Round any approximate solutions to three decimal places.