Question: Repeat Problem 69 with the cost and
Repeat Problem 69 with the cost and revenue equations
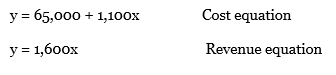
Data from problem 69:
A small plant manufactures riding lawn mowers. The plant has fixed costs (leases, insurance, etc.) of $48,000 per day and variable costs (labor, materials, etc.) of $1,400 per unit produced. The mowers are sold for $1,800 each. So the cost and revenue equations are
y = 48,000 + 1,400x Cost equation
y = 1,800x Revenue equation
where x is the total number of mowers produced and sold each day. The daily costs and revenue are in dollars.
> In how many ways can 3 people sit in a row of 7 chairs?
> Solve by Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Using augmented matrix methods.
> Five distinct points are selected on the circumference of a circle. (A) How many line segments can be drawn by joining the points in all possible ways? (B) How many triangles can be drawn using these 5 points as vertices? (C) How many quadrilaterals c
> Using augmented matrix methods.
> Each of the matrices in below Problems is the final matrix form for a system of two linear equations in the variables x1 and x2. Write the solution of the system.
> Each of the matrices in below Problems is the final matrix form for a system of two linear equations in the variables x1 and x2. Write the solution of the system.
> Each of the matrices in below Problem is the final matrix form for a system of two linear equations in the variables x1 and x2. Write the solution of the system. Answer: x1 ( 3 , x2 ( (5
> Using augmented matrix methods. Write the linear system represented by each augmented matrix in your solution, and solve each of these systems graphically. Discuss the relationships among the solutions of these systems.
> Using augmented matrix methods. Graph each solution set. Discuss the differences between the graph of an equation in the system and the graph of the system’s solution set.
> Using augmented matrix methods. Graph each solution set. Discuss the differences between the graph of an equation in the system and the graph of the system’s solution set.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Discuss the validity of each statement. If the statement is true, explain why. If not, give a counter example. If n and r are positive integers and 1 < r < n, then nPr = nPn - r.
> Each of the matrices in below Problem is the result of performing a single row operation on the matrix A shown below. Identify the row operation.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix.
> Perform the row operations indicated in below Problem on the following matrix. Answer:
> Write the system of linear equations that is represented by the given augmented matrix. Assume that the variables are x1 and x2.
> Write the system of linear equations that is represented by the given augmented matrix. Assume that the variables are x1 and x2.
> Write the coefficient matrix and the augmented matrix of the given system of linear equations.
> Discuss the validity of each statement. If the statement is true, explain why. If not, give a counter example. If n and r are positive integers and 1 < r < n, then nCr < nCr + 1.
> Write the coefficient matrix and the augmented matrix of the given system of linear equations.
> Refer to the following matrices: For matrix D, find d11 + d21
> Refer to the following matrices: For matrix A, list the elements a21, a12.
> Find an equation in point–slope form, y - y1 = m(x - x1), of the line through the given points. (3, 20) and 1 -5, 42.
> Find the x and y coordinates of the intersection of the given lines. 6x - 5y = 120 and y = 3
> Find the x and y coordinates of the intersection of the given lines. 3x + 4y = 72 and the y axis
> Find the x and y coordinates of the intersection of the given lines. y = 5x + 7 and the x axis
> A ship using sound-sensing devices above and below water recorded a surface explosion 6 seconds sooner by its underwater device than its above-water device. Sound travels in air at 1,100 feet per second and in seawater at 5,000 feet per second. How long
> Repeat Problem 81 if the object is 240 feet above the ground after 1 second and 192 feet above the ground after 2 seconds. Data from 81: An object dropped off the top of a tall building falls vertically with constant acceleration. If s is the distance o
> A company produces Italian sausages and bratwursts at plants in Green Bay and Sheboygan. The hourly production rates at each plant are given in the table. How many hours should each plant operate to exactly fill an order for 62,250 Italian sausages and 7
> Discuss the validity of each statement. If the statement is true, explain why. If not, give a counter example. If n is a positive integer greater than 3, then n! > 2n.
> A fruit grower uses two types of fertilizer in an orange grove, brand A and brand B. Each bag of brand A contains 8 pounds of nitrogen and 4 pounds of phosphoric acid. Each bag of brand B contains 7 pounds of nitrogen and 6 pounds of phosphoric acid. Tes
> Refer to Problem 75. (A) If the company decides to discontinue production of the robust blend and produce only the mild blend, how many pounds of the mild blend can the company produce? How many beans of each type will the company use? Are there any bea
> Refer to Problem 73. Federated Shipping, a competing overnight delivery service, informs the customer in Problem 73 that they would ship the 5-pound package for $29.95 and the 20-pound package for $59.20. (A) If Federated Shipping computes its cost in t
> Repeat Problem 71 if the monthly fixed costs increase to $27,200, the variable costs increase to $9.15, and the company raises the selling price of the DVDs to $21.95 Data from 71: A company markets exercise DVDs that sell for $19.95, including shipping
> At $2.13 per bushel, the annual supply for corn in the Midwest is 8.9 billion bushels and the annual demand is 6.5 billion bushels. When the price falls to $1.50 per bushel, the annual supply decreases to 8.2 billion bushels and the annual demand increas
> Suppose that the supply and demand for printed baseball caps for a particular week are / where p is the price in dollars and q is the quantity in hundreds. (A) Find the supply and demand (to the nearest unit) if baseball caps are $4 each. Discuss the s
> Repeat Problem 63 for the following systems: (A) 6x - 5y = 10 -13x + 11y = -20 (B) 6x - 5y = 10 -13x + 10y = -20 (C) 6x - 5y = 10 -12x + 10y = -20 Data from Problem 63: The coefficients of the three systems given below are similar. One might gue
> Graph the equations in the same coordinate system. Find the coordinates of any points where two or more lines intersect. Is there a point that is a solution to all three equations?
> Graph the equations in the same coordinate system. Find the coordinates of any points where two or more lines intersect. Is there a point that is a solution to all three equations?
> Refer to the table in the graphing calculator display below, which shows y1 = nPr and y2 = nCr for n = 6. Explain how the table illustrates the formula nPr = r!nCr
> Graph the equations in the same coordinate system. Find the coordinates of any points where two or more lines intersect. Is there a point that is a solution to all three equations?
> Use a graphing calculator to find the solution to each system. Round any approximate solutions to three decimal places.
> Use a graphing calculator to find the solution to each system. Round any approximate solutions to three decimal places.
> Use a graphing calculator to find the solution to each system. Round any approximate solutions to three decimal places.
> Problems are concerned with the linear system. If m = 0, how many solutions does the system have?
> Problems are concerned with the linear system. If the system has no solution, discuss the relationships among the four constants.
> In a free competitive market, if the demand for a good is greater than the supply, will the price tend to go up or come down?
> Note that each solution can be found mentally, without the use of a calculator or pencil-andpaper calculation; try to visualize the graphs of both lines.
> Note that each solution can be found mentally, without the use of a calculator or pencil-andpaper calculation; try to visualize the graphs of both lines.
> Three departments have 12, 15, and 18 members, respectively. If each department selects a delegate and an alternate to represent the department at a conference, how many ways can this be done?
> Note that each solution can be found mentally, without the use of a calculator or pencil-andpaper calculation; try to visualize the graphs of both lines.
> Note that each solution can be found mentally, without the use of a calculator or pencil-andpaper calculation; try to visualize the graphs of both lines.
> Solve Problem using substitution or elimination by addition.
> Solve Problem using substitution or elimination by addition.
> Solve Problem using substitution or elimination by addition.
> Solve Problem using substitution or elimination by addition.
> Solve Problem using substitution or elimination by addition.
> Solve Problem using elimination by addition.
> Solve Problem using elimination by addition.
> Solve Problems using substitution.
> From a standard 52-card deck, how many 5-card hands contain 5 different ranks of cards?
> Evaluate the expression. If the answer is not an integer, round to four decimal places.
> Solve Problems using substitution.
> Solve Problems by graphing.
> Solve Problems by graphing.
> Match each system in Below Problems with one of the following graphs, and use the graph to solve the system.
> Match each system in Below Problems with one of the following graphs, and use the graph to solve the system.
> Find the sum of the finite geometric series a + ar + ar2 + …+ arn 1 -. Write the answer as a quotient of integers.
> Find the sum of the finite geometric series a + ar + ar2 + …+ arn 1 -. Write the answer as a quotient of integers.
> Find the sum of the finite geometric series a + ar + ar2 + …+ arn 1 -. Write the answer as a quotient of integers.
> Use graphical approximation techniques or an equation solver to approximate the desired interest rate. Express each answer as a percentage, correct to two decimal places. At the time they retire, a couple has $200,000 invested in an annuity. The couple c
> Use graphical approximation techniques or an equation solver to approximate the desired interest rate. Express each answer as a percentage, correct to two decimal places. A $2,000 computer can be financed by paying $100 per month for 2 years. What is the
> From a standard 52-card deck, how many 4-card hands consist of cards from the same suit?
> Discuss the similarities and differences in the graphs of unpaid balance as a function of time for 30-year mortgages of $60,000 at rates of 7%, 10%, and 13%, respectively (see the figure). Include computations of the monthly payment and total interest pa
> A person purchased a $200,000 home 20 years ago by paying 20% down and signing a 30-year mortgage at 13.2% compounded monthly. Interest rates have dropped and the owner wants to refinance the unpaid balance by signing a new 10-year mortgage at 8.2% compo
> A person purchased a house 10 years ago for $160,000. The house was financed by paying 20% down and signing a 30-year mortgage at 7.75% on the unpaid balance. Equal monthly payments were made to amortize the loan over a 30- year period. The owner now (af
> An ordinary annuity pays 6.48% compounded monthly. (A) A person wants to make equal monthly deposits into the account for 15 years in order to then make equal monthly withdrawals of $1,500 for the next 20 years, reducing the balance to zero. How much sh
> Refer to Problem 55. If the account owner decides to withdraw $3,000 monthly, how much is in the account after 10 years? After 20 years? After 30 years? Data from Problem 55: An ordinary annuity that earns 7.5% compounded monthly has a current balance o
> At the time they retire, a couple has $200,000 in an account that pays 8.4% compounded monthly. (A) If the couple decides to withdraw equal monthly payments for 10 years, at the end of which time the account will have a zero balance, how much should the
> A family has a $210,000, 20-year mortgage at 6.75% compounded monthly. Find the monthly payment. Also find the unpaid balance after (A) 5 years (B) 10 years (C) 15 years
> A person establishes a sinking fund for retirement by contributing $7,500 per year at the end of each year for 20 years. For the next 20 years, equal yearly payments are withdrawn, at the end of which time the account will have a zero balance. If money i
> A family is thinking about buying a new house costing $120,000. The family must pay 20% down, and the rest is to be amortized over 30 years in equal monthly payments. If money costs 7.5% compounded monthly, what will the monthly payment be? How much tota
> A man establishes an annuity for retirement by depositing $50,000 into an account that pays 7.2% compounded monthly. Equal monthly withdrawals will be made each month for 5 years, at which time the account will have a zero balance. Each year taxes must b
> From a standard 52-card deck, how many 7-card hands consist of 3 hearts and 4 diamonds?
> Construct the amortization schedule for a $10,000 debt that is to be amortized in six equal quarterly payments at 2.6% interest per quarter on the unpaid balance.

