Question: In a study conducted at Virginia Tech
In a study conducted at Virginia Tech on the development of ectomycorrhizal, a symbiotic relationship between the roots of trees and a fungus, in which minerals are transferred from the fungus to the trees and sugars from the trees to the fungus, 20 northern red oak seedlings exposed to the fungus Pisolithus tinctorus were grown in a greenhouse. All seedlings were planted in the same type of soil and received the same amount of sunshine and water. Half received no nitrogen at planting time, to serve as a control, and the other half received 368 ppm of nitrogen in the form NaNO3. The stem weights, in grams, at the end of 140 days were recorded as follows:
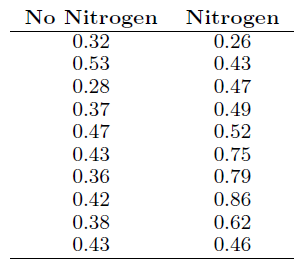
Construct a 95% confidence interval for the difference in the mean stem weight between seedlings that receive no nitrogen and those that receive 368 ppm of nitrogen. Assume the populations to be normally distributed with equal variances.
Transcribed Image Text:
No Nitrogen 0.32 Nitrogen 0.26 0.53 0.43 0.28 0.47 0.37 0.49 0.47 0.52 0.43 0.75 0.36 0.79 0.42 0.86 0.38 0.62 0.43 0.46
> Consider a random sample of x1, . . . , xn from a uniform distribution U(0, θ) with unknown parameter θ, where θ > 0. Determine the maximum likelihood estimator of θ.
> Consider a random sample of x1, x2, . . . , xn observations from a Weibull distribution with parameters α and β and density function / (a) Write out the likelihood function. (b) Write out the equations that, when solved, give the maximum likelihood
> Consider a random sample of x1, . . . , xn coming from the gamma distribution discussed in Section 6.6. Suppose the parameter α is known, say 5, and determine the maximum likelihood estimation for parameter β.
> Consider the lognormal distribution with the density function given in Section 6.9. Suppose we have a random sample x1, x2, . . . , xn from a lognormal distribution. (a) Write out the likelihood function. (b) Develop the maximum likelihood estimators o
> Suppose that there are n trials x1, x2, . . . , xn from a Bernoulli process with parameter p, the probability of a success. That is, the probability of r successes is given by Work out the maximum likelihood estimator for the parameter p. (:)p"(1
> Construct a 95% confidence interval for σ2A/σ2B in Exercise 9.49 on page 295. Should the equal-variance assumption be used? Exercise 9.49: Two different brands of latex paint are being considered for use. Fifteen specimens of each
> An efficiency expert wishes to determine the average time that it takes to drill three holes in a certain metal clamp. How large a sample will she need to be 95% confident that her sample mean will be within 15 seconds of the true mean? Assume that it is
> Construct a 90% confidence interval for σ21/σ22 in Exercise 9.46 on page 295. Should we have assumed σ21 = σ22 in constructing our confidence interval for μI − μII?
> Construct a 90% confidence interval for σ21/σ22 in Exercise 9.43 on page 295. Were we justified in assuming that σ21 ≠ σ22 when we constructed the confidence interval for μ1 − μ2? Exercise 9.43: A taxi company is trying to decide whether to purchase bra
> Construct a 98% confidence interval for σ1/σ2 in Exercise 9.42 on page 295, where σ1 and σ2 are, respectively, the standard deviations for the distances traveled per liter of fuel by the Volkswagen and Toyota mini-trucks. Exercise 9.42: An experiment re
> Construct a 90% confidence interval for σ in Exercise 9.13 on page 283. Exercise 9.13: A random sample of 12 shearing pins is taken in a study of the Rockwell hardness of the pin head. Measurements on the Rockwell hardness are made for each of the 12, y
> Construct a 99% confidence interval for σ in Exercise 9.12 on page 283. Exercise 9.12: A random sample of 10 chocolate energy bars of a certain brand has, on average, 230 calories per bar, with a standard deviation of 15 calories. Construct a 99% confid
> Construct a 99% confidence interval for σ2 in Exercise 9.11 on page 283. Exercise 9.11: A machine produces metal pieces that are cylindrical in shape. A sample of pieces is taken, and the diameters are found to be 1.01, 0.97, 1.03, 1.04, 0.99, 0.98, 0.9
> Construct a 95% confidence interval for σ2 in Exercise 9.9 on page 283. Exercise 9.9: Regular consumption of presweetened cereals contributes to tooth decay, heart disease, and other degenerative diseases, according to studies conducted by Dr. W. H. Bow
> A random sample of 20 students yielded a mean of ¯x = 72 and a variance of s2 = 16 for scores on a college placement test in mathematics. Assuming the scores to be normally distributed, construct a 98% confidence interval for σ2.
> A manufacturer of car batteries claims that the batteries will last, on average, 3 years with a variance of 1 year. If 5 of these batteries have lifetimes of 1.9, 2.4, 3.0, 3.5, and 4.2 years, construct a 95% confidence interval for σ2 and decide if the
> According to USA Today (March 17, 1997), women made up 33.7% of the editorial staff at local TV stations in the United States in 1990 and 36.2% in 1994. Assume 20 new employees were hired as editorial staff. (a) Estimate the number that would have been w
> How large a sample is needed in Exercise 9.3 if we wish to be 95% confident that our sample mean will be within 0.0005 inch of the true mean? Exercise 9.3 Many cardiac patients wear an implanted pacemaker to control their heartbeat. A plastic connector
> A survey of 1000 students found that 274 chose professional baseball team A as their favorite team. In a similar survey involving 760 students, 240 of them chose team A as their favorite. Compute a 95% confidence interval for the difference between the p
> In the study Germination and Emergence of Broccoli, conducted by the Department of Horticulture at Virginia Tech, a researcher found that at 5◦ C, 10 broccoli seeds out of 20 germinated, while at 15◦ C, 15 out of 20 germinated. Compute a 95% confidence i
> A clinical trial was conducted to determine if a certain type of inoculation has an effect on the incidence of a certain disease. A sample of 1000 rats was kept in a controlled environment for a period of 1 year, and 500 of the rats were given the inocul
> Ten engineering schools in the United States were surveyed. The sample contained 250 electrical engineers, 80 being women; 175 chemical engineers, 40 being women. Compute a 90% confidence interval for the difference between the proportions of women in th
> A certain geneticist is interested in the proportion of males and females in the population who have a minor blood disorder. In a random sample of 1000 males, 250 are found to be afflicted, whereas 275 of 1000 females tested appear to have the disorder.
> A study is to be made to estimate the proportion of residents of a certain city and its suburbs who favor the construction of a nuclear power plant near the city. How large a sample is needed if one wishes to be at least 95% confident that the estimate i
> A study is to be made to estimate the percentage of citizens in a town who favor having their water fluoridated. How large a sample is needed if one wishes to be at least 95% confident that the estimate is within 1% of the true percentage?
> A conjecture by a faculty member in the microbiology department at Washington University School of Dental Medicine in St. Louis, Missouri, states that a couple of cups of either green or oolong tea each day will provide sufficient fluoride to protect you
> How large a sample is needed in Exercise 9.52 if we wish to be 98% confident that our sample proportion will be within 0.05 of the true proportion defective? Exercise 9.52: Compute 95% confidence intervals, using both methods on page 297, for the propor
> How large a sample is needed if we wish to be 99% confident that our sample proportion in Exercise 9.51 will be within 0.05 of the true proportion of homes in the city that are heated by oil? Exercise 9.51: In a random sample of 1000 homes in a certain
> How large a sample is needed in Exercise 9.2 if we wish to be 96% confident that our sample mean will be within 10 hours of the true mean? Exercise 9.2 An electrical firm manufactures light bulbs that have a length of life that is approximately normally
> How large a sample is needed if we wish to be 96% confident that our sample proportion in Exercise 9.53 will be within 0.02 of the true fraction of the voting population? Exercise 9.53: (a) A random sample of 200 voters in a town is selected, and 114 ar
> In the newspaper article referred to in Exercise 9.57, 32% of the 1600 adults polled said the U.S. space program should emphasize scientific exploration. How large a sample of adults is needed for the poll if one wishes to be 95% confident that the estim
> (a) According to a report in the Roanoke Times & World-News, approximately 2/3 of 1600 adults polled by telephone said they think the space shuttle program is a good investment for the country. Find a 95% confidence interval for the proportion of America
> A geneticist is interested in the proportion of African males who have a certain minor blood disorder. In a random sample of 100 African males, 24 are found to be afflicted. (a) Compute a 99% confidence interval for the proportion of African males who ha
> A new rocket-launching system is being considered for deployment of small, short-range rockets. The existing system has p = 0.8 as the probability of a successful launch. A sample of 40 experimental launches is made with the new system, and 34 are succes
> A manufacturer of MP3 players conducts a set of comprehensive tests on the electrical functions of its product. All MP3 players must pass all tests prior to being sold. Of a random sample of 500 MP3 players, 15 failed one or more tests. Find a 90% confid
> (a) A random sample of 200 voters in a town is selected, and 114 are found to support an annexation suit. Find the 96% confidence interval for the fraction of the voting population favoring the suit. (b) What can we assert with 96% confidence about the p
> Compute 95% confidence intervals, using both methods on page 297, for the proportion of defective items in a process when it is found that a sample of size 100 yields 8 defectives.
> In a random sample of 1000 homes in a certain city, it is found that 228 are heated by oil. Find 99% confidence intervals for the proportion of homes in this city that are heated by oil using both methods presented on page 297.
> Two levels (low and high) of insulin doses are given to two groups of diabetic rats to check the insulin binding capacity, yielding the following data: Low dose: n1 = 8 ¯x1 = 1.98 s1 = 0.51 High dose: n2 = 13 ¯x2 = 1.30 s2 = 0.35 Assume that the variance
> A random sample of 100 automobile owners in the state of Virginia shows that an automobile is driven on average 23,500 kilometers per year with a standard deviation of 3900 kilometers. Assume the distribution of measurements to be approximately normal. (
> Two different brands of latex paint are being considered for use. Fifteen specimens of each type of paint were selected, and the drying times, in hours, were as follows: Assume the drying time is normally distributed with σA = σB.
> An automotive company is considering two types of batteries for its automobile. Sample information on battery life is collected for 20 batteries of type A and 20 batteries of type B. The summary statistics are ¯xA = 32.91, ¯xB = 30.47, sA = 1.57, and sB
> Fortune magazine (March 1997) reported the total returns to investors for the 10 years prior to 1996 and also for 1996 for 431 companies. The total returns for 10 of the companies are listed below. Find a 95% confidence interval for the mean change in pe
> The following data represent the running times of films produced by two motion-picture companies. Compute a 90% confidence interval for the difference between the average running times of films produced by the two companies. Assume that the running-tim
> The federal government awarded grants to the agricultural departments of 9 universities to test the yield capabilities of two new varieties of wheat. Each variety was planted on a plot of equal area at each university, and the yields, in kilograms per pl
> Referring to Exercise 9.43, find a 99% confidence interval for μ1 − μ2 if tires of the two brands are assigned at random to the left and right rear wheels of 8 taxis and the following distances, in kilometers
> A taxi company is trying to decide whether to purchase brand A or brand B tires for its fleet of taxis. To estimate the difference in the two brands, an experiment is conducted using 12 of each brand. The tires are run until they wear out. The results ar
> An experiment reported in Popular Science compared fuel economies for two types of similarly equipped diesel mini-trucks. Let us suppose that 12 Volkswagen and 10 Toyota trucks were tested in 90- kilometer-per-hour steady-paced trials. If the 12 Volkswag
> The following data represent the length of time, in days, to recovery for patients randomly treated with one of two medications to clear up severe bladder infections: Find a 99% confidence interval for the difference μ2−
> The heights of a random sample of 50 college students showed a mean of 174.5 centimeters and a standard deviation of 6.9 centimeters. (a) Construct a 98% confidence interval for the mean height of all college students. (b) What can we assert with 98% con
> Students may choose between a 3-semester-hour physics course without labs and a 4-semester-hour course with labs. The final written examination is the same for each section. If 12 students in the section with labs made an average grade of 84 with a stand
> Two catalysts in a batch chemical process, are being compared for their effect on the output of the process reaction. A sample of 12 batches was prepared using catalyst 1, and a sample of 10 batches was prepared using catalyst 2. The 12 batches for which
> A study was conducted to determine if a certain treatment has any effect on the amount of metal removed in a pickling operation. A random sample of 100 pieces was immersed in a bath for 24 hours without the treatment, yielding an average of 12.2 millimet
> Two kinds of thread are being compared for strength. Fifty pieces of each type of thread are tested under similar conditions. Brand A has an average tensile strength of 78.3 kilograms with a standard deviation of 5.6 kilograms, while brand B has an avera
> A random sample of size n1 = 25, taken from a normal population with a standard deviation σ1 = 5, has a mean ¯x1 = 80. A second random sample of size n2 = 36, taken from a different normal population with a standard deviation σ2 = 3, has a mean ¯x2 = 75.
> Consider Exercise 9.33. Use the MSE discussed in Exercise 9.28 to determine which estimator is more efficient. Write out MSE(S2) / MSE(S’2).
> Compare S2 and S ‘2 (see Exercise 9.29), the two estimators of σ2, to determine which is more efficient. Assume these estimators are found using X1,X2, . . . , Xn, independent random variables from n(x; μ, σ). Which estimator is more efficient considerin
> Show that the estimator P’ of Exercise 9.31(b) becomes unbiased as n→∞.
> If X is a binomial random variable, show that (a) ^P = X/n is an unbiased estimator of p; (b) P’ = X+√n/2 / n+√n is a biased estimator of p.
> Consider S’2, the estimator of σ2, from Exercise 9.29. Analysts often use S’2 rather than dividing the degrees of freedom in the sample. (a) What is the bias of S’2? (b) Show that the bia
> Many cardiac patients wear an implanted pacemaker to control their heartbeat. A plastic connector module mounts on the top of the pacemaker. Assuming a standard deviation of 0.0015 inch and an approximately normal distribution, find a 95% confidence inte
> The weights of a large number of miniature poodles are approximately normally distributed with a mean of 8 kilograms and a standard deviation of 0.9 kilogram. If measurements are recorded to the nearest tenth of a kilogram, find the fraction of these poo
> Suppose X follows a continuous uniform distribution from 1 to 5. Determine the conditional probability P(X >2.5 | X ≤ 4).
> A company pays its employees an average wage of $15.90 an hour with a standard deviation of $1.50. If the wages are approximately normally distributed and paid to the nearest cent, (a) what percentage of the workers receive wages between $13.75 and $16.2
> The heights of 1000 students are normally distributed with a mean of 174.5 centimeters and a standard deviation of 6.9 centimeters. Assuming that the heights are recorded to the nearest half-centimeter, how many of these students would you expect to have
> The average life of a certain type of small motor is 10 years with a standard deviation of 2 years. The manufacturer replaces free all motors that fail while under guarantee. If she is willing to replace only 3% of the motors that fail, how long a guaran
> In the November 1990 issue of Chemical Engineering Progress, a study discussed the percent purity of oxygen from a certain supplier. Assume that the mean was 99.61 with a standard deviation of 0.08. Assume that the distribution of percent purity was appr
> A lawyer commutes daily from his suburban home to his midtown office. The average time for a one-way trip is 24 minutes, with a standard deviation of 3.8 minutes. Assume the distribution of trip times to be normally distributed. (a) What is the probabili
> Let us define Show that and hence S’2 is a biased estimator for σ2. * = Ë(X, - X)*/n. S'2 i=1 E(S") = [(n – 1)/n]o°, [(n – 1)/n]o², ||
> The finished inside diameter of a piston ring is normally distributed with a mean of 10 centimeters and a standard deviation of 0.03 centimeter. (a) What proportion of rings will have inside diameters exceeding 10.075 centimeters? (b) What is the probabi
> A research scientist reports that mice will live an average of 40 months when their diets are sharply restricted and then enriched with vitamins and proteins. Assuming that the lifetimes of such mice are normally distributed with a standard deviation of
> The loaves of rye bread distributed to local stores by a certain bakery have an average length of 30 centimeters and a standard deviation of 2 centimeters. Assuming that the lengths are normally distributed, what percentage of the loaves are (a) longer t
> Consider the data in Exercise 8.2, find (a) the range; (b) the standard deviation. Exercise 8.2: The lengths of time, in minutes, that 10 patients waited in a doctor’s office before receiving treatment were recorded as follows: 5, 11, 9, 5, 10, 15, 6, 1
> A soft-drink machine is regulated so that it discharges an average of 200 milliliters per cup. If the amount of drink is normally distributed with a standard deviation equal to 15 milliliters, (a) what fraction of the cups will contain more than 224 mill
> According to Chebyshev’s theorem, the probability that any random variable assumes a value within 3 standard deviations of the mean is at least 8/9. If it is known that the probability distribution of a random variable X is normal with mean μ and varianc
> Given a continuous uniform distribution, show that (a) μ =(A+B)/2 and (b) σ2 = ((B-A)2)/12
> The length of time, in seconds, that a computer user takes to read his or her e-mail is distributed as a lognormal random variable with μ = 1.8 and σ2 = 4.0. (a) What is the probability that a user reads e-mail for more than 20 seconds? More than a minut
> From the relationship between the chi-squared random variable and the gamma random variable, prove that the mean of the chi-squared random variable is v and the variance is 2v.
> Explain why the nature of the scenario in Review Exercise 6.82 would likely not lend itself to the exponential distribution. Exercise 6.82: The length of life, in hours, of a drill bit in a mechanical operation has a Weibull distribution with α = 2 and
> In Section 9.3, we emphasized the notion of “most efficient estimator” by comparing the variance of two unbiased estimators ˆΘ1 and ˆΘ2. However, this does not take into ac
> Derive the cdf for the Weibull distribution.
> The length of life, in hours, of a drill bit in a mechanical operation has a Weibull distribution with α = 2 and β = 50. Find the probability that the bit will fail before 10 hours of usage.
> The length of time between breakdowns of an essential piece of equipment is important in the decision of the use of auxiliary equipment. An engineer thinks that the best model for time between breakdowns of a generator is the exponential distribution wit
> In a human factor experimental project, it has been determined that the reaction time of a pilot to a visual stimulus is normally distributed with a mean of 1/2 second and standard deviation of 2/5 second. (a) What is the probability that a reaction from
> According to ecology writer Jacqueline Killeen, phosphates contained in household detergents pass right through our sewer systems, causing lakes to turn into swamps that eventually dry up into deserts. The following data show the amount of phosphates per
> Consider Review Exercise 6.78. Given the assumption of the exponential distribution, what is the mean number of calls per hour? What is the variance in the number of calls per hour? Exercise 6.78: Consider now Review Exercise 3.74 on page 108. The densi
> Consider now Review Exercise 3.74 on page 108. The density function of the time Z in minutes between calls to an electrical supply store is given by (a) What is the mean time between calls? (b) What is the variance in the time between calls? (c) What i
> The beta distribution has considerable application in reliability problems in which the basic random variable is a proportion, as in the practical scenario illustrated in Exercise 6.50 on page 206. In that regard, consider Review Exercise 3.73 on page 10
> In Exercise 6.54 on page 206, the lifetime of a transistor is assumed to have a gamma distribution with mean 10 weeks and standard deviation √50 weeks. Suppose that the gamma distribution assumption is incorrect. Assume that the distribution is normal. (
> Consider the situation in Review Exercise 8.74. Suppose a considerable effort is conducted to “tighten” the variability in the system. Following the effort, a random sample of size 40 is taken from the new assembly line and the sample variance is s2 = 0.
> Consider the situation of Case Study 9.1 on page 281 with a larger sample of metal pieces. The diameters are as follows: 1.01, 0.97, 1.03, 1.04, 0.99, 0.98, 1.01, 1.03, 0.99, 1.00, 1.00, 0.99, 0.98, 1.01, 1.02, 0.99 centimeters. Once again the normality
> Suppose a filling machine is used to fill cartons with a liquid product. The specification that is strictly enforced for the filling machine is 9 ± 1.5 oz. If any carton is produced with weight outside these bounds, it is considered by the supplier to be
> In Chapter 9, the concept of parameter estimation will be discussed at length. Suppose X is a random variable with mean μ and variance σ2 = 1.0. Suppose also that a random sample of size n is to be taken and ¯x is to be used as an estimate of μ. When the
> Given a normal random variable X with mean 20 and variance 9, and a random sample of size n taken from the distribution, what sample size n is necessary in order that P(19.9 ≤ ¯X ≤ 20.1) = 0.95?
> From the information in Review Exercise 8.70, compute (assuming μB = 65%) P(¯XB ≥ 70).
> A random sample of employees from a local manufacturing plant pledged the following donations, in dollars, to the United Fund: 100, 40, 75, 15, 20, 100, 75, 50, 30, 10, 55, 75, 25, 50, 90, 80, 15, 25, 45, and 100. Calculate (a) the mean; (b) the mode.
> Two distinct solid fuel propellants, type A and type B, are being considered for a space program activity. Burning rates of the propellant are crucial. Random samples of 20 specimens of the two propellants are taken with sample means 20.5 cm/sec for prop
> Consider the situation of Review Exercise 8.62. If the population from which the sample was taken has population mean μ = 53, 000 kilometers, does the sample information here seem to support that claim? In your answer, compute and determi
> The breaking strength X of a certain rivet used in a machine engine has a mean 5000 psi and standard deviation 400 psi. A random sample of 36 rivets is taken. Consider the distribution of ¯X, the sample mean breaking strength. (a) What is the probability
> Consider Review Exercise 8.56. Comment on any outliers in the data.

