Question: In Section 9.3, we emphasized the
In Section 9.3, we emphasized the notion of “most efficient estimator†by comparing the variance of two unbiased estimators ˆΘ1 and ˆΘ2. However, this does not take into account bias in case one or both estimators are not unbiased. Consider the quantity
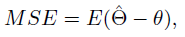
where MSE denotes mean squared error. The MSE is often used to compare two estimators ˆΘ1 and ˆΘ2 of θ when either or both is unbiased because
(i) it is intuitively reasonable and
(ii) it accounts for bias. Show that MSE can be written
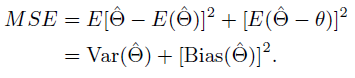
Transcribed Image Text:
MSE = E(Ô – 0), MSE = E[Ô – E(Ô)]² + [E(Ô – 0)]² = Var(Ô) + [Bias(Ô)]².
> (a) According to a report in the Roanoke Times & World-News, approximately 2/3 of 1600 adults polled by telephone said they think the space shuttle program is a good investment for the country. Find a 95% confidence interval for the proportion of America
> A geneticist is interested in the proportion of African males who have a certain minor blood disorder. In a random sample of 100 African males, 24 are found to be afflicted. (a) Compute a 99% confidence interval for the proportion of African males who ha
> A new rocket-launching system is being considered for deployment of small, short-range rockets. The existing system has p = 0.8 as the probability of a successful launch. A sample of 40 experimental launches is made with the new system, and 34 are succes
> A manufacturer of MP3 players conducts a set of comprehensive tests on the electrical functions of its product. All MP3 players must pass all tests prior to being sold. Of a random sample of 500 MP3 players, 15 failed one or more tests. Find a 90% confid
> (a) A random sample of 200 voters in a town is selected, and 114 are found to support an annexation suit. Find the 96% confidence interval for the fraction of the voting population favoring the suit. (b) What can we assert with 96% confidence about the p
> Compute 95% confidence intervals, using both methods on page 297, for the proportion of defective items in a process when it is found that a sample of size 100 yields 8 defectives.
> In a random sample of 1000 homes in a certain city, it is found that 228 are heated by oil. Find 99% confidence intervals for the proportion of homes in this city that are heated by oil using both methods presented on page 297.
> Two levels (low and high) of insulin doses are given to two groups of diabetic rats to check the insulin binding capacity, yielding the following data: Low dose: n1 = 8 ¯x1 = 1.98 s1 = 0.51 High dose: n2 = 13 ¯x2 = 1.30 s2 = 0.35 Assume that the variance
> A random sample of 100 automobile owners in the state of Virginia shows that an automobile is driven on average 23,500 kilometers per year with a standard deviation of 3900 kilometers. Assume the distribution of measurements to be approximately normal. (
> Two different brands of latex paint are being considered for use. Fifteen specimens of each type of paint were selected, and the drying times, in hours, were as follows: Assume the drying time is normally distributed with σA = σB.
> An automotive company is considering two types of batteries for its automobile. Sample information on battery life is collected for 20 batteries of type A and 20 batteries of type B. The summary statistics are ¯xA = 32.91, ¯xB = 30.47, sA = 1.57, and sB
> Fortune magazine (March 1997) reported the total returns to investors for the 10 years prior to 1996 and also for 1996 for 431 companies. The total returns for 10 of the companies are listed below. Find a 95% confidence interval for the mean change in pe
> The following data represent the running times of films produced by two motion-picture companies. Compute a 90% confidence interval for the difference between the average running times of films produced by the two companies. Assume that the running-tim
> The federal government awarded grants to the agricultural departments of 9 universities to test the yield capabilities of two new varieties of wheat. Each variety was planted on a plot of equal area at each university, and the yields, in kilograms per pl
> Referring to Exercise 9.43, find a 99% confidence interval for μ1 − μ2 if tires of the two brands are assigned at random to the left and right rear wheels of 8 taxis and the following distances, in kilometers
> A taxi company is trying to decide whether to purchase brand A or brand B tires for its fleet of taxis. To estimate the difference in the two brands, an experiment is conducted using 12 of each brand. The tires are run until they wear out. The results ar
> An experiment reported in Popular Science compared fuel economies for two types of similarly equipped diesel mini-trucks. Let us suppose that 12 Volkswagen and 10 Toyota trucks were tested in 90- kilometer-per-hour steady-paced trials. If the 12 Volkswag
> The following data represent the length of time, in days, to recovery for patients randomly treated with one of two medications to clear up severe bladder infections: Find a 99% confidence interval for the difference μ2−
> In a study conducted at Virginia Tech on the development of ectomycorrhizal, a symbiotic relationship between the roots of trees and a fungus, in which minerals are transferred from the fungus to the trees and sugars from the trees to the fungus, 20 nort
> The heights of a random sample of 50 college students showed a mean of 174.5 centimeters and a standard deviation of 6.9 centimeters. (a) Construct a 98% confidence interval for the mean height of all college students. (b) What can we assert with 98% con
> Students may choose between a 3-semester-hour physics course without labs and a 4-semester-hour course with labs. The final written examination is the same for each section. If 12 students in the section with labs made an average grade of 84 with a stand
> Two catalysts in a batch chemical process, are being compared for their effect on the output of the process reaction. A sample of 12 batches was prepared using catalyst 1, and a sample of 10 batches was prepared using catalyst 2. The 12 batches for which
> A study was conducted to determine if a certain treatment has any effect on the amount of metal removed in a pickling operation. A random sample of 100 pieces was immersed in a bath for 24 hours without the treatment, yielding an average of 12.2 millimet
> Two kinds of thread are being compared for strength. Fifty pieces of each type of thread are tested under similar conditions. Brand A has an average tensile strength of 78.3 kilograms with a standard deviation of 5.6 kilograms, while brand B has an avera
> A random sample of size n1 = 25, taken from a normal population with a standard deviation σ1 = 5, has a mean ¯x1 = 80. A second random sample of size n2 = 36, taken from a different normal population with a standard deviation σ2 = 3, has a mean ¯x2 = 75.
> Consider Exercise 9.33. Use the MSE discussed in Exercise 9.28 to determine which estimator is more efficient. Write out MSE(S2) / MSE(S’2).
> Compare S2 and S ‘2 (see Exercise 9.29), the two estimators of σ2, to determine which is more efficient. Assume these estimators are found using X1,X2, . . . , Xn, independent random variables from n(x; μ, σ). Which estimator is more efficient considerin
> Show that the estimator P’ of Exercise 9.31(b) becomes unbiased as n→∞.
> If X is a binomial random variable, show that (a) ^P = X/n is an unbiased estimator of p; (b) P’ = X+√n/2 / n+√n is a biased estimator of p.
> Consider S’2, the estimator of σ2, from Exercise 9.29. Analysts often use S’2 rather than dividing the degrees of freedom in the sample. (a) What is the bias of S’2? (b) Show that the bia
> Many cardiac patients wear an implanted pacemaker to control their heartbeat. A plastic connector module mounts on the top of the pacemaker. Assuming a standard deviation of 0.0015 inch and an approximately normal distribution, find a 95% confidence inte
> The weights of a large number of miniature poodles are approximately normally distributed with a mean of 8 kilograms and a standard deviation of 0.9 kilogram. If measurements are recorded to the nearest tenth of a kilogram, find the fraction of these poo
> Suppose X follows a continuous uniform distribution from 1 to 5. Determine the conditional probability P(X >2.5 | X ≤ 4).
> A company pays its employees an average wage of $15.90 an hour with a standard deviation of $1.50. If the wages are approximately normally distributed and paid to the nearest cent, (a) what percentage of the workers receive wages between $13.75 and $16.2
> The heights of 1000 students are normally distributed with a mean of 174.5 centimeters and a standard deviation of 6.9 centimeters. Assuming that the heights are recorded to the nearest half-centimeter, how many of these students would you expect to have
> The average life of a certain type of small motor is 10 years with a standard deviation of 2 years. The manufacturer replaces free all motors that fail while under guarantee. If she is willing to replace only 3% of the motors that fail, how long a guaran
> In the November 1990 issue of Chemical Engineering Progress, a study discussed the percent purity of oxygen from a certain supplier. Assume that the mean was 99.61 with a standard deviation of 0.08. Assume that the distribution of percent purity was appr
> A lawyer commutes daily from his suburban home to his midtown office. The average time for a one-way trip is 24 minutes, with a standard deviation of 3.8 minutes. Assume the distribution of trip times to be normally distributed. (a) What is the probabili
> Let us define Show that and hence S’2 is a biased estimator for σ2. * = Ë(X, - X)*/n. S'2 i=1 E(S") = [(n – 1)/n]o°, [(n – 1)/n]o², ||
> The finished inside diameter of a piston ring is normally distributed with a mean of 10 centimeters and a standard deviation of 0.03 centimeter. (a) What proportion of rings will have inside diameters exceeding 10.075 centimeters? (b) What is the probabi
> A research scientist reports that mice will live an average of 40 months when their diets are sharply restricted and then enriched with vitamins and proteins. Assuming that the lifetimes of such mice are normally distributed with a standard deviation of
> The loaves of rye bread distributed to local stores by a certain bakery have an average length of 30 centimeters and a standard deviation of 2 centimeters. Assuming that the lengths are normally distributed, what percentage of the loaves are (a) longer t
> Consider the data in Exercise 8.2, find (a) the range; (b) the standard deviation. Exercise 8.2: The lengths of time, in minutes, that 10 patients waited in a doctor’s office before receiving treatment were recorded as follows: 5, 11, 9, 5, 10, 15, 6, 1
> A soft-drink machine is regulated so that it discharges an average of 200 milliliters per cup. If the amount of drink is normally distributed with a standard deviation equal to 15 milliliters, (a) what fraction of the cups will contain more than 224 mill
> According to Chebyshev’s theorem, the probability that any random variable assumes a value within 3 standard deviations of the mean is at least 8/9. If it is known that the probability distribution of a random variable X is normal with mean μ and varianc
> Given a continuous uniform distribution, show that (a) μ =(A+B)/2 and (b) σ2 = ((B-A)2)/12
> The length of time, in seconds, that a computer user takes to read his or her e-mail is distributed as a lognormal random variable with μ = 1.8 and σ2 = 4.0. (a) What is the probability that a user reads e-mail for more than 20 seconds? More than a minut
> From the relationship between the chi-squared random variable and the gamma random variable, prove that the mean of the chi-squared random variable is v and the variance is 2v.
> Explain why the nature of the scenario in Review Exercise 6.82 would likely not lend itself to the exponential distribution. Exercise 6.82: The length of life, in hours, of a drill bit in a mechanical operation has a Weibull distribution with α = 2 and
> Derive the cdf for the Weibull distribution.
> The length of life, in hours, of a drill bit in a mechanical operation has a Weibull distribution with α = 2 and β = 50. Find the probability that the bit will fail before 10 hours of usage.
> The length of time between breakdowns of an essential piece of equipment is important in the decision of the use of auxiliary equipment. An engineer thinks that the best model for time between breakdowns of a generator is the exponential distribution wit
> In a human factor experimental project, it has been determined that the reaction time of a pilot to a visual stimulus is normally distributed with a mean of 1/2 second and standard deviation of 2/5 second. (a) What is the probability that a reaction from
> According to ecology writer Jacqueline Killeen, phosphates contained in household detergents pass right through our sewer systems, causing lakes to turn into swamps that eventually dry up into deserts. The following data show the amount of phosphates per
> Consider Review Exercise 6.78. Given the assumption of the exponential distribution, what is the mean number of calls per hour? What is the variance in the number of calls per hour? Exercise 6.78: Consider now Review Exercise 3.74 on page 108. The densi
> Consider now Review Exercise 3.74 on page 108. The density function of the time Z in minutes between calls to an electrical supply store is given by (a) What is the mean time between calls? (b) What is the variance in the time between calls? (c) What i
> The beta distribution has considerable application in reliability problems in which the basic random variable is a proportion, as in the practical scenario illustrated in Exercise 6.50 on page 206. In that regard, consider Review Exercise 3.73 on page 10
> In Exercise 6.54 on page 206, the lifetime of a transistor is assumed to have a gamma distribution with mean 10 weeks and standard deviation √50 weeks. Suppose that the gamma distribution assumption is incorrect. Assume that the distribution is normal. (
> Consider the situation in Review Exercise 8.74. Suppose a considerable effort is conducted to “tighten” the variability in the system. Following the effort, a random sample of size 40 is taken from the new assembly line and the sample variance is s2 = 0.
> Consider the situation of Case Study 9.1 on page 281 with a larger sample of metal pieces. The diameters are as follows: 1.01, 0.97, 1.03, 1.04, 0.99, 0.98, 1.01, 1.03, 0.99, 1.00, 1.00, 0.99, 0.98, 1.01, 1.02, 0.99 centimeters. Once again the normality
> Suppose a filling machine is used to fill cartons with a liquid product. The specification that is strictly enforced for the filling machine is 9 ± 1.5 oz. If any carton is produced with weight outside these bounds, it is considered by the supplier to be
> In Chapter 9, the concept of parameter estimation will be discussed at length. Suppose X is a random variable with mean μ and variance σ2 = 1.0. Suppose also that a random sample of size n is to be taken and ¯x is to be used as an estimate of μ. When the
> Given a normal random variable X with mean 20 and variance 9, and a random sample of size n taken from the distribution, what sample size n is necessary in order that P(19.9 ≤ ¯X ≤ 20.1) = 0.95?
> From the information in Review Exercise 8.70, compute (assuming μB = 65%) P(¯XB ≥ 70).
> A random sample of employees from a local manufacturing plant pledged the following donations, in dollars, to the United Fund: 100, 40, 75, 15, 20, 100, 75, 50, 30, 10, 55, 75, 25, 50, 90, 80, 15, 25, 45, and 100. Calculate (a) the mean; (b) the mode.
> Two distinct solid fuel propellants, type A and type B, are being considered for a space program activity. Burning rates of the propellant are crucial. Random samples of 20 specimens of the two propellants are taken with sample means 20.5 cm/sec for prop
> Consider the situation of Review Exercise 8.62. If the population from which the sample was taken has population mean μ = 53, 000 kilometers, does the sample information here seem to support that claim? In your answer, compute and determi
> The breaking strength X of a certain rivet used in a machine engine has a mean 5000 psi and standard deviation 400 psi. A random sample of 36 rivets is taken. Consider the distribution of ¯X, the sample mean breaking strength. (a) What is the probability
> Consider Review Exercise 8.56. Comment on any outliers in the data.
> Consider the data in Exercise 9.13. Suppose the manufacturer of the shearing pins insists that the Rockwell hardness of the product be less than or equal to 44.0 only 5% of the time. What is your reaction? Use a tolerance limit calculation as the basis f
> Consider Example 1.5 on page 25. Comment on any outliers.
> If S21 and S22 represent the variances of independent random samples of size n1 = 25 and n2 = 31, taken from normal populations with variances σ21 = 10 and σ22 = 15, respectively, find P(S21/S22 > 1.26).
> Consider the data of Exercise 1.19 on page 31. Construct a box-and-whisker plot. Comment. Compute the sample mean and sample standard deviation. Exercise 1.19 The following data represent the length of life in years, measured to the nearest tenth, of 30
> A taxi company tests a random sample of 10 steel-belted radial tires of a certain brand and records the following tread wear: 48,000, 53,000, 45,000, 61,000, 59,000, 56,000, 63,000, 49,000, 53,000, and 54,000 kilometers. Use the results of Exercise 8.14
> If the number of hurricanes that hit a certain area of the eastern United States per year is a random variable having a Poisson distribution with μ = 6, find the probability that this area will be hit by (a) exactly 15 hurricanes in 2 years; (b) at most
> A random sample of 5 bank presidents indicated annual salaries of $395,000, $521,000, $483,000, $479,000, and $510,000. Find the variance of this set.
> Find the mean, median, and mode for the sample whose observations, 15, 7, 8, 95, 19, 12, 8, 22, and 14, represent the number of sick days claimed on 9 federal income tax returns. Which value appears to be the best measure of the center of these data? Sta
> If S21 and S22 represent the variances of independent random samples of size n1 = 8 and n2 = 12, taken from normal populations with equal variances, find P(S21/S22 < 4.89).
> In testing for carbon monoxide in a certain brand of cigarette, the data, in milligrams per cigarette, were coded by subtracting 12 from each observation. Use the results of Exercise 8.14 on page 231 to find the standard deviation for the carbon monoxide
> If X1,X2, . . . , Xn are independent random variables having identical exponential distributions with parameter θ, show that the density function of the random variable Y = X1+X2+· · ·+Xn is that of a gamma distribution with parameters α = n and β = θ.
> Consider the drying time measurements in Exercise 9.14. Suppose the 15 observations in the data set are supplemented by a 16th value of 6.9 hours. In the context of the original 15 observations, is the 16th value an outlier? Show work. Exercise 9.14: Th
> Consider the data displayed in Exercise 1.20 on page 31. Construct a box-and-whisker plot and comment on the nature of the sample. Compute the sample mean and sample standard deviation.
> Computer response time is an important application of the gamma and exponential distributions. Suppose that a study of a certain computer system reveals that the response time, in seconds, has an exponential distribution with a mean of 3 seconds. (a) Wha
> Construct a quantile plot of these data, which represent the lifetimes, in hours, of fifty 40-watt, 110- volt internally frosted incandescent lamps taken from forced life tests: 919 1196 785 1126 936 918 1156 920 948 1067 1092 1162 1170 929 950 905
> Consider the following measurements of the heat-producing capacity of the coal produced by two mines (in millions of calories per ton): Mine 1: 8260 8130 8350 8070 8340 Mine 2: 7950 7890 7900 8140 7920 7840 Can it be concluded that the two population v
> Pull-strength tests on 10 soldered leads for a semiconductor device yield the following results, in pounds of force required to rupture the bond: Another set of 8 leads was tested after encapsulation to determine whether the pull strength had been incr
> For an F-distribution, find (a) f0.05 with v1 = 7 and v2 = 15; (b) f0.05 with v1 = 15 and v2 = 7: (c) f0.01 with v1 = 24 and v2 = 19; (d) f0.95 with v1 = 19 and v2 = 24; (e) f0.99 with v1 = 28 and v2 = 12.
> A maker of a certain brand of low-fat cereal bars claims that the average saturated fat content is 0.5 gram. In a random sample of 8 cereal bars of this brand, the saturated fat content was 0.6, 0.7, 0.7, 0.3, 0.4, 0.5, 0.4, and 0.2. Would you agree with
> The numbers of incorrect answers on a true-false competency test for a random sample of 15 students were recorded as follows: 2, 1, 3, 0, 1, 3, 6, 0, 3, 3, 5, 2, 1, 4, and 2. Find (a) the mean; (b) the median; (c) the mode.
> A normal population with unknown variance has a mean of 20. Is one likely to obtain a random sample of size 9 from this population with a mean of 24 and a standard deviation of 4.1? If not, what conclusion would you draw?
> A manufacturing firm claims that the batteries used in their electronic games will last an average of 30 hours. To maintain this average, 16 batteries are tested each month. If the computed t-value falls between −t0.025 and t0.025, the firm is satisfied
> Refer to Exercise 9.22 again. Suppose that specifications by a buyer of the thread are that the tensile strength of the material must be at least 62 kilograms. The manufacturer is satisfied if at most 5% of the manufactured pieces have tensile strength l
> Given a random sample of size 24 from a normal distribution, find k such that (a) P(−2.069 < T < k) = 0.965; (b) P(k < T < 2.807) = 0.095; (c) P(−k < T < k) = 0.90.
> (a) Find P(−t0.005 < T < t0.01) for v = 20. (b) Find P(T > −t0.025).
> (a) Find P(T < 2.365) when v = 7. (b) Find P(T > 1.318) when v = 24. (c) Find P(−1.356 < T < 2.179) when v = 12. (d) Find P(T > −2.567) when v = 17.
> (a) Find t0.025 when v = 14. (b) Find −t0.10 when v = 10. (c) Find t0.995 when v = 7.
> Show that the variance of S2 for random samples of size n from a normal population decreases as n becomes large.
> The scores on a placement test given to college freshmen for the past five years are approximately normally distributed with a mean μ = 74 and a variance σ2 = 8. Would you still consider σ2 = 8 to be a valid value of the variance if a random sample of 20
> Assume the sample variances to be continuous measurements. Find the probability that a random sample of 25 observations, from a normal population with variance σ2 = 6, will have a sample variance S2 (a) greater than 9.1; (b) between 3.462 and 10.745.
> For a chi-squared distribution, find χ2α such that (a) P(X2 > χ2α) = 0.01 when v = 21; (b) P(X2 < χ2α) = 0.95 when v = 6; (c) P(χ2α < X2 < 23.209) = 0.015 when v = 10.

