Question: In Exercise 3.13 on page 92,
In Exercise 3.13 on page 92, the distribution of the number of imperfections per 10 meters of synthetic fabric is given by
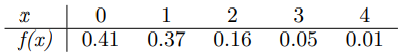
(a) Plot the probability function.
(b) Find the expected number of imperfections, E(X) = μ.
(c) Find E(X2).
Transcribed Image Text:
1 2 3 0.01 4 f(x) | 0.41 0.37 0.16 0.05
> A nationwide survey of 17,000 college seniors by the University of Michigan revealed that almost 70% disapprove of daily pot smoking. If 18 of these seniors are selected at random and asked their opinion, what is the probability that more than 9 but fewe
> The length of time Y, in minutes, required to generate a human reflex to tear gas has the density function (a) What is the mean time to reflex? (b) Find E(Y2) and Var(Y ). Sie-/4, 0<y < , f(y) [ 0, elsewhere.
> Consider Review Exercise 3.64 on page 107. There are two service lines. The random variables X and Y are the proportions of time that line 1 and line 2 are in use, respectively. The joint probability density function for (X, Y ) is given by (a) Determi
> By investing in a particular stock, a person can make a profit in one year of $4000 with probability 0.3 or take a loss of $1000 with probability 0.7. What is this person’s expected gain?
> Consider Review Exercise 3.77 on page 108. The random variables X and Y represent the number of vehicles that arrive at two separate street corners during a certain 2-minute period in the day. The joint distribution is (a) Give E(X), E(Y ), Var(X), and
> The power P in watts which is dissipated in an electric circuit with resistance R is known to be given by P = I2R, where I is current in amperes and R is a constant fixed at 50 ohms. However, I is a random variable with μI = 15 amperes and σ2I = 0.03 amp
> If the joint density function of X and Y is given by find the expected value of S{ 0 < x < 1, 1< y < 2, (x + 2y), f (x, y) = 10, elsewhere, g() = + X?Y. X, Y
> Let X represent the number that occurs when a green die is tossed and Y the number that occurs when a red die is tossed. Find the variance of the random variable (a) 2X − Y; (b) X + 3Y − 5.
> Let X represent the number that occurs when a red die is tossed and Y the number that occurs when a green die is tossed. Find (a) E(X + Y ); (b) E(X − Y ); (c) E(XY ).
> Suppose that X and Y are independent random variables with probability densities and and Find the expected value of Z = XY . x > 2, [0, g(x) elsewhere, 2y, 0<y < 1, h(y) 0, elsewhere.
> Repeat Exercise 4.62 if X and Y are not independent and σXY = 1. Exercise 4.62: If X and Y are independent random variables with variances σ2X = 5 and σ2Y = 3, find the variance of the random variable Z = −2X + 4Y − 3.
> It is estimated that 4000 of the 10,000 voting residents of a town are against a new sales tax. If 15 eligible voters are selected at random and asked their opinion, what is the probability that at most 7 favor the new tax?
> In a certain city district, the need for money to buy drugs is stated as the reason for 75% of all thefts. Find the probability that among the next 5 theft cases reported in this district, (a) exactly 2 resulted from the need for money to buy drugs; (b)
> If X and Y are independent random variables with variances σ2X = 5 and σ2Y = 3, find the variance of the random variable Z = −2X + 4Y − 3.
> Use Theorem 4.7 to evaluate E(2XY2 − X2Y ) for the joint probability distribution shown in Table 3.1 on page 96.
> Suppose that X and Y are independent random variables having the joint probability distribution Find (a) E(2X − 3Y ); (b) E(XY ). f(x, y) 4 0.10 0.15 3 0.20 1 0.30 0.10 0.15
> An attendant at a car wash is paid according to the number of cars that pass through. Suppose the probabilities are 1/12, 1/12, 1/4, 1/4, 1/6, and 1/6, respectively, that the attendant receives $7, $9, $11, $13, $15, or $17 between 4:00 P.M. and 5:00 P.M
> If a random variable X is defined such that E[(X − 1)2] = 10 and E[(X − 2)2 ]=6, find μ and σ2.
> The total time, measured in units of 100 hours, that a teenager runs her hair dryer over a period of one year is a continuous random variable X that has the density function Use Theorem 4.6 to evaluate the mean of the random variable Y = 60X2 + 39X, wh
> Let X be a random variable with the following probability distribution: Find E(X) and E(X2) and then, using these values, evaluate E[(2X + 1)2]. -3 6 9 f (x) 6 3
> Repeat Exercise 4.43 on page 127 by applying Theorem 4.5 and Corollary 4.6. Exercise 4.43: The length of time, in minutes, for an airplane to obtain clearance for takeoff at a certain airport is a random variable Y = 3X −2, where X has
> Suppose that a grocery store purchases 5 cartons of skim milk at the wholesale price of $1.20 per carton and retails the milk at $1.65 per carton. After the expiration date, the unsold milk is removed from the shelf and the grocer receives a credit from
> Using Theorem 4.5 and Corollary 4.6, find the mean and variance of the random variable Z = 5X + 3, where X has the probability distribution of Exercise 4.36 on page 127. Exercise 4.36: Suppose that the probabilities are 0.4, 0.3, 0.2, and 0.1, respectiv
> An annexation suit against a county subdivision of 1200 residences is being considered by a neighboring city. If the occupants of half the residences object to being annexed, what is the probability that in a random sample of 10 at least 3 favor the anne
> Referring to Exercise 4.35 on page 127, find the mean and variance of the discrete random variable Z = 3X − 2, when X represents the number of errors per 100 lines of code. Exercise 4.35: The random variable X, representing the number
> Random variables X and Y follow a joint distribution Determine the correlation coefficient between X and Y . (2, 0 <x <y < 1, 0, otherwise. f (x, y) =
> For the random variables X and Y in Exercise 3.39 on page 105, determine the correlation coefficient between X and Y . Exercise 3.39: From a sack of fruit containing 3 oranges, 2 apples, and 3 bananas, a random sample of 4 pieces of fruit is selected. I
> For a laboratory assignment, if the equipment is working, the density function of the observed outcome X is Find the variance and standard deviation of X. 2(1 — 2), 0 <х<1, (0, f (x) = otherwise.
> In a gambling game, a woman is paid $3 if she draws a jack or a queen and $5 if she draws a king or an ace from an ordinary deck of 52 playing cards. If she draws any other card, she loses. How much should she pay to play if the game is fair?
> Consider the situation in Exercise 4.32 on page 119. The distribution of the number of imperfections per 10 meters of synthetic failure is given by Find the variance and standard deviation of the number of imperfections. 1 3 4 f(x) 0.41 0.37 0.16 0
> Given a random variable X, with standard deviation σX, and a random variable Y = a + bX, show that if b < 0, the correlation coefficient ρXY = −1, and if b > 0, ρXY = 1.
> For the random variables X and Y whose joint density function is given in Exercise 3.40 on page 105, find the covariance.
> Find the covariance of the random variables X and Y of Exercise 3.44 on page 105.
> Find the covariance of the random variables X and Y of Exercise 3.49 on page 106.
> Among 150 IRS employees in a large city, only 30 are women. If 10 of the employees are chosen at random to provide free tax assistance for the residents of this city, use the binomial approximation to the hypergeometric distribution to find the probabili
> Find the covariance of the random variables X and Y of Exercise 3.39 on page 105.
> The length of time, in minutes, for an airplane to obtain clearance for takeoff at a certain airport is a random variable Y = 3X −2, where X has the density function Find the mean and variance of the random variable Y . Sie-/4, x
> Using the results of Exercise 4.21 on page 118, find the variance of g(X) = X2, where X is a random variable having the density function given in Exercise 4.12 on page 117.
> Find the standard deviation of the random variable g(X) = (2X + 1)2 in Exercise 4.17 on page 118.
> Referring to Exercise 4.14 on page 117, find σ2(X) for the function g(X)=3X2 + 4.
> A coin is biased such that a head is three times as likely to occur as a tail. Find the expected number of tails when this coin is tossed twice.
> The total number of hours, in units of 100 hours, that a family runs a vacuum cleaner over a period of one year is a random variable X having the density function given in Exercise 4.13 on page 117. Find the variance of X.
> The proportion of people who respond to a certain mail-order solicitation is a random variable X having the density function given in Exercise 4.14 on page 117. Find the variance of X.
> A dealer’s profit, in units of $5000, on a new automobile is a random variable X having the density function given in Exercise 4.12 on page 117. Find the variance of X.
> Suppose that the probabilities are 0.4, 0.3, 0.2, and 0.1, respectively, that 0, 1, 2, or 3 power failures will strike a certain subdivision in any given year. Find the mean and variance of the random variable X representing the number of power failures
> Suppose that the manufacturing company of Exercise 5.36 decides to change its acceptance scheme. Under the new scheme, an inspector takes 1 item at random, inspects it, and then replaces it in the box; a second inspector does likewise. Finally, a third i
> The random variable X, representing the number of errors per 100 lines of software code, has the following probability distribution: Using Theorem 4.2 on page 121, find the variance of X. 2 3 4 5 f(x) | 0.01 0.25 0.4 0.3 0.04
> Let X be a random variable with the following probability distribution: Find the standard deviation of X. -2 3 5 f(x) 0.3 0.2 0.5
> Use Definition 4.3 on page 120 to find the variance of the random variable X of Exercise 4.7 on page 117.
> Consider Exercise 3.32 on page 94. (a) What is the mean proportion of the budget allocated to environmental and pollution control? (b) What is the probability that a company selected at random will have allocated to environmental and pollution control a
> In Exercise 3.31 on page 94, the distribution of times before a major repair of a washing machine was given as What is the population mean of the times to repair? Sie-v/4, y 2 0, f(y) : (0, elsewhere.
> Find the mean of the random variable T representing the total of the three coins in Exercise 3.25 on page 93.
> Exercise 3.29 on page 93 dealt with an important particle size distribution characterized by (a) Plot the density function. (b) Give the mean particle size. -4 f(x) = S3x¯ x > 1, elsewhere.
> Consider the information in Exercise 3.28 on page 93. The problem deals with the weight in ounces of the product in a cereal box, with (a) Plot the density function. (b) Compute the expected value, or mean weight, in ounces. (c) Are you surprised at yo
> In Exercise 3.27 on page 93, a density function is given for the time to failure of an important component of a DVD player. Find the mean number of hours to failure of the component and thus the DVD player.
> A manufacturing company uses an acceptance scheme on items from a production line before they are shipped. The plan is a two-stage one. Boxes of 25 items are readied for shipment, and a sample of 3 items is tested for defectives. If any defectives are fo
> Referring to the random variables whose joint probability distribution is given in Exercise 3.51 on page 106, find the mean for the total number of jacks and kings when 3 cards are drawn without replacement from the 12 face cards of an ordinary deck of 5
> Referring to the random variables whose joint probability distribution is given in Exercise 3.39 on page 105, (a) find E(X2Y − 2XY ); (b) find μX − μY .
> Suppose that X and Y have the following joint probability function: (a) Find the expected value of g(X, Y ) = XY2. (b) Find μX and μY . f(x, y) 4 1 0.10 0.15 3 0.20 0.30 0.10 0.15
> The hospitalization period, in days, for patients following treatment for a certain type of kidney disorder is a random variable Y = X + 4, where X has the density function Find the average number of days that a person is hospitalized following treatme
> What is the dealer’s average profit per automobile if the profit on each automobile is given by g(X) = X2, where X is a random variable having the density function of Exercise 4.12?
> A continuous random variable X has the density function Find the expected value of g(X) = e2X/3. x > 0, 0, f (x) : elsewhere.
> The probability distribution of the discrete random variable X is Find the mean of X. 3-r 3 3 f (x) : x = 0,1,2, 3. 4
> A large industrial firm purchases several new word processors at the end of each year, the exact number depending on the frequency of repairs in the previous year. Suppose that the number of word processors, X, purchased each year has the following proba
> Find the expected value of the random variable g(X) = X2, where X has the probability distribution of Exercise 4.2.
> A company is interested in evaluating its current inspection procedure for shipments of 50 identical items. The procedure is to take a sample of 5 and pass the shipment if no more than 2 are found to be defective. What proportion of shipments with 20% de
> Let X be a random variable with the following probability distribution: Find μg(X), where g(X) = (2X + 1)2. -3 6 9 f (x) 1/6 1/2 1/3
> Suppose that you are inspecting a lot of 1000 light bulbs, among which 20 are defectives. You choose two light bulbs randomly from the lot without replacement. Let Find the probability that at least one light bulb chosen is defective. 1, if the 1st
> Assume that two random variables (X, Y) are uniformly distributed on a circle with radius a. Then the joint probability density function is Find μX, the expected value of X. S , a? +y? < a?, f(x, y) 10, otherwise.
> Find the proportion X of individuals who can be expected to respond to a certain mail-order solicitation if X has the density function 2(x+2) 0 < x < 1, f (x) = 0, elsewhere.
> The density function of the continuous random variable X, the total number of hours, in units of 100 hours, that a family runs a vacuum cleaner over a period of one year, is given in Exercise 3.7 on page 92 as Find the average number of hours per year
> If a dealer’s profit, in units of $5000, on a new automobile can be looked upon as a random variable X having the density function find the average profit per automobile. S 2(1 – x), 0<< x < 1, (0, f(x) = elsewhere,
> The density function of coded measurements of the pitch diameter of threads of a fitting is Find the expected value of X. 4 0 < x < 1, f (x) = T(1+x²)' 0, elsewhere.
> Consider Review Exercise 3.73 on page 108. It involved Y, the proportion of impurities in a batch, and the density function is given by (a) Find the expected percentage of impurities. (b) Find the expected value of the proportion of quality material (i
> As we shall illustrate in Chapter 12, statistical methods associated with linear and nonlinear models are very important. In fact, exponential functions are often used in a wide variety of scientific and engineering problems. Consider a model that is fit
> Two tire-quality experts examine stacks of tires and assign a quality rating to each tire on a 3-point scale. Let X denote the rating given by expert A and Y denote the rating given by B. The following table gives the joint distribution for X and Y. Fi
> What is the probability that a waitress will refuse to serve alcoholic beverages to only 2 minors if she randomly checks the IDs of 5 among 9 students, 4 of whom are minors?
> The probability distribution of X, the number of imperfections per 10 meters of a synthetic fabric in continuous rolls of uniform width, is given in Exercise 3.13 on page 92 as x 01234 Find the average number of imperfections per 10 meters of this fabr
> Suppose that the four inspectors at a film factory are supposed to stamp the expiration date on each package of film at the end of the assembly line. John, who stamps 20% of the packages, fails to stamp the expiration date once in every 200 packages; Tom
> If the person in Exercise 2.96 received a speeding ticket on her way to work, what is the probability that she passed through the radar trap located at L2? Exercise 2.96: Police plan to enforce speed limits by using radar traps at four different locatio
> Referring to Exercise 2.95, what is the probability that a person diagnosed as having cancer actually has the disease? Exercise 2.95: In a certain region of the country it is known from past experience that the probability of selecting an adult over 40
> Police plan to enforce speed limits by using radar traps at four different locations within the city limits. The radar traps at each of the locations L1, L2, L3, and L4 will be operated 40%, 30%, 20%, and 30% of the time. If a person who is speeding on h
> In a certain region of the country it is known from past experience that the probability of selecting an adult over 40 years of age with cancer is 0.05. If the probability of a doctor correctly diagnosing a person with cancer as having the disease is 0.7
> In the situation of Exercise 2.93, it is known that the system does not work. What is the probability that the component A also does not work?
> A circuit system is given in Figure 2.11. Assume the components fail independently. (a) What is the probability that the entire system works? (b) Given that the system works, what is the probability that the component A is not working? Figure 2.11:
> Suppose the diagram of an electrical system is as given in Figure 2.10. What is the probability that the system works? Assume the components fail independently. Figure 2.10: 0.7 B 0.95 0.9 A D 0.8 Figure 2.10: Diagram for Exercise 2.92.
> Find the probability of randomly selecting 4 good quarts of milk in succession from a cooler containing 20 quarts of which 5 have spoiled, by using (a) the first formula of Theorem 2.12 on page 68; (b) the formulas of Theorem 2.6 and Rule 2.3 on pages 50
> If 7 cards are dealt from an ordinary deck of 52 playing cards, what is the probability that (a) exactly 2 of them will be face cards? (b) at least 1 of them will be a queen?
> Pollution of the rivers in the United States has been a problem for many years. Consider the following events: A: the river is polluted, B: a sample of water tested detects pollution, C: fishing is permitted. Assume P(A) = 0.3, P(B|A) = 0.75, P(B|A’) = 0
> The proportion of people who respond to a certain mail-order solicitation is a continuous random variable X that has the density function (a) Show that P(0 (b) Find the probability that more than 1/4 but fewer than 1/2 of the people contacted will resp
> A town has two fire engines operating independently. The probability that a specific engine is available when needed is 0.96. (a) What is the probability that neither is available when needed? (b) What is the probability that a fire engine is available w
> Before the distribution of certain statistical software, every fourth compact disk (CD) is tested for accuracy. The testing process consists of running four independent programs and checking the results. The failure rates for the four testing programs ar
> A real estate agent has 8 master keys to open several new homes. Only 1 master key will open any given house. If 40% of these homes are usually left unlocked, what is the probability that the real estate agent can get into a specific home if the agent se
> In 1970, 11% of Americans completed four years of college; 43% of them were women. In 1990, 22% of Americans completed four years of college; 53% of them were women (Time, Jan. 19, 1996). (a) Given that a person completed four years of college in 1970, w
> The probability that a doctor correctly diagnoses a particular illness is 0.7. Given that the doctor makes an incorrect diagnosis, the probability that the patient files a lawsuit is 0.9. What is the probability that the doctor makes an incorrect diagnos
> The probability that the head of a household is home when a telemarketing representative calls is 0.4. Given that the head of the house is home, the probability that goods will be bought from the company is 0.3. Find the probability that the head of the
> The probability that a vehicle entering the Luray Caverns has Canadian license plates is 0.12; the probability that it is a camper is 0.28; and the probability that it is a camper with Canadian license plates is 0.09. What is the probability that (a) a c
> For married couples living in a certain suburb, the probability that the husband will vote on a bond referendum is 0.21, the probability that the wife will vote on the referendum is 0.28, and the probability that both the husband and the wife will vote i
> From a lot of 10 missiles, 4 are selected at random and fired. If the lot contains 3 defective missiles that will not fire, what is the probability that (a) all 4 will fire? (b) at most 2 will not fire?
> The probability that a married man watches a certain television show is 0.4, and the probability that a married woman watches the show is 0.5. The probability that a man watches the show, given that his wife does, is 0.7. Find the probability that (a) a

