Question: Referring to Exercise 4.35 on page
Referring to Exercise 4.35 on page 127, find the mean and variance of the discrete random variable Z = 3X − 2, when X represents the number of errors per 100 lines of code.
Exercise 4.35:
The random variable X, representing the number of errors per 100 lines of software code, has the following probability distribution:
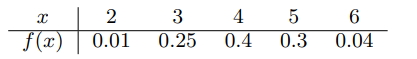
Using Theorem 4.2 on page 121, find the variance of X.
Transcribed Image Text:
2 3 4 5 f(x) | 0.01 0.25 0.4 0.3 0.04
> Consider Exercise 4.10 on page 117. Can it be said that the ratings given by the two experts are independent? Explain why or why not. Exercise 4.10: Two tire-quality experts examine stacks of tires and assign a quality rating to each tire on a 3-point s
> A dealer’s profit, in units of $5000, on a new automobile is a random variable X having density function (a) Find the variance of the dealer’s profit. (b) Demonstrate that Chebyshev’s theorem holds
> Consider random variables X and Y of Exercise 4.63 on page 138. Compute ρXY. Exercise 4.63: Repeat Exercise 4.62 if X and Y are not independent and σXY = 1. Exercise 4.62: If X and Y are independent random variables with variances σ2X = 5 and σ2Y = 3, f
> A foreign student club lists as its members 2 Canadians, 3 Japanese, 5 Italians, and 2 Germans. If a committee of 4 is selected at random, find the probability that (a) all nationalities are represented; (b) all nationalities except Italian are represent
> A private pilot wishes to insure his airplane for $200,000. The insurance company estimates that a total loss will occur with probability 0.002, a 50% loss with probability 0.01, and a 25% loss with probability 0.1. Ignoring all other partial losses, wha
> Consider the joint density function Compute the correlation coefficient ρXY. 16у , x > 2, 0 < y < 1, (0, f (x, y) = elsewhere.
> Consider the density function of Review Exercise 4.85. Demonstrate that Chebyshev’s theorem holds for k = 2 and k = 3. Review Exercise 4.85: Suppose it is known that the life X of a particular compressor, in hours, has the density func
> Show that Cov(aX, bY ) = ab Cov(X, Y ).
> Referring to the random variables whose joint density function is given in Exercise 3.40 on page 105, (a) find μX and μY ; (b) find E[(X + Y )/2].
> Suppose it is known that the life X of a particular compressor, in hours, has the density function (a) Find the mean life of the compressor. (b) Find E(X2). (c) Find the variance and standard deviation of the random variable X. 1/900 e 900 x > 0, f
> Referring to the random variables whose joint probability density function is given in Exercise 3.41 on page 105, find the expected weight for the sum of the creams and toffees if one purchased a box of these chocolates.
> Referring to the random variables whose joint density function is given in Exercise 3.41 on page 105, find the covariance between the weight of the creams and the weight of the toffees in these boxes of chocolates.
> Assume the length X, in minutes, of a particular type of telephone conversation is a random variable with probability density function (a) Determine the mean length E(X) of this type of telephone conversation. (b) Find the variance and standard deviati
> Referring to the random variables whose joint probability density function is given in Exercise 3.47 on page 105, find the average amount of kerosene left in the tank at the end of the day.
> Find the probability of being dealt a bridge hand of 13 cards containing 5 spades, 2 hearts, 3 diamonds, and 3 clubs.
> Find the covariance of random variables X and Y having the joint probability density function Sx + y, 0< x < 1, 0 < y < 1, [0, f(x, y) elsewhere.
> Suppose that an antique jewelry dealer is interested in purchasing a gold necklace for which the probabilities are 0.22, 0.36, 0.28, and 0.14, respectively, that she will be able to sell it for a profit of $250, sell it for a profit of $150, break even,
> Prove Chebyshev’s theorem.
> Compute P(μ − 2σ and compare with the result given in Chebyshev’s theorem. J бх (1 — а), 0 <х <1, 0, f (x) = elsewhere,
> A random variable X has a mean μ = 10 and a variance σ2 = 4. Using Chebyshev’s theorem, find (a) P(|X − 10| ≥ 3); (b) P(|X − 10| < 3); (c) P(5
> Seventy new jobs are opening up at an automobile manufacturing plant, and 1000 applicants show up for the 70 positions. To select the best 70 from among the applicants, the company gives a test that covers mechanical skill, manual dexterity, and mathemat
> An electrical firm manufactures a 100-watt light bulb, which, according to specifications written on the package, has a mean life of 900 hours with a standard deviation of 50 hours. At most, what percentage of the bulbs fail to last even 700 hours? Assum
> Consider again the situation of Exercise 4.72. It is required to find Var(eY ). Use Theorems 4.2 and 4.3 and define Z = eY . Thus, use the conditions of Exercise 4.73 to find Var(Z) = E(Z2 ) − [E(Z)]2 .
> For the situation in Exercise 4.72, compute E(eY ) using Theorem 4.1, that is, by using Then compute E(eY ) not by using f(y), but rather by using the second-order adjustment to the first-order approximation of E(eY ). Comment. E(e*) = | e" f(y) dy
> A manufacturing company has developed a machine for cleaning carpet that is fuel-efficient because it delivers carpet cleaner so rapidly. Of interest is a random variable Y, the amount in gallons per minute delivered. It is known that the density functio
> A nationwide survey of 17,000 college seniors by the University of Michigan revealed that almost 70% disapprove of daily pot smoking. If 18 of these seniors are selected at random and asked their opinion, what is the probability that more than 9 but fewe
> The length of time Y, in minutes, required to generate a human reflex to tear gas has the density function (a) What is the mean time to reflex? (b) Find E(Y2) and Var(Y ). Sie-/4, 0<y < , f(y) [ 0, elsewhere.
> Consider Review Exercise 3.64 on page 107. There are two service lines. The random variables X and Y are the proportions of time that line 1 and line 2 are in use, respectively. The joint probability density function for (X, Y ) is given by (a) Determi
> By investing in a particular stock, a person can make a profit in one year of $4000 with probability 0.3 or take a loss of $1000 with probability 0.7. What is this person’s expected gain?
> Consider Review Exercise 3.77 on page 108. The random variables X and Y represent the number of vehicles that arrive at two separate street corners during a certain 2-minute period in the day. The joint distribution is (a) Give E(X), E(Y ), Var(X), and
> The power P in watts which is dissipated in an electric circuit with resistance R is known to be given by P = I2R, where I is current in amperes and R is a constant fixed at 50 ohms. However, I is a random variable with μI = 15 amperes and σ2I = 0.03 amp
> If the joint density function of X and Y is given by find the expected value of S{ 0 < x < 1, 1< y < 2, (x + 2y), f (x, y) = 10, elsewhere, g() = + X?Y. X, Y
> Let X represent the number that occurs when a green die is tossed and Y the number that occurs when a red die is tossed. Find the variance of the random variable (a) 2X − Y; (b) X + 3Y − 5.
> Let X represent the number that occurs when a red die is tossed and Y the number that occurs when a green die is tossed. Find (a) E(X + Y ); (b) E(X − Y ); (c) E(XY ).
> Suppose that X and Y are independent random variables with probability densities and and Find the expected value of Z = XY . x > 2, [0, g(x) elsewhere, 2y, 0<y < 1, h(y) 0, elsewhere.
> Repeat Exercise 4.62 if X and Y are not independent and σXY = 1. Exercise 4.62: If X and Y are independent random variables with variances σ2X = 5 and σ2Y = 3, find the variance of the random variable Z = −2X + 4Y − 3.
> It is estimated that 4000 of the 10,000 voting residents of a town are against a new sales tax. If 15 eligible voters are selected at random and asked their opinion, what is the probability that at most 7 favor the new tax?
> In a certain city district, the need for money to buy drugs is stated as the reason for 75% of all thefts. Find the probability that among the next 5 theft cases reported in this district, (a) exactly 2 resulted from the need for money to buy drugs; (b)
> If X and Y are independent random variables with variances σ2X = 5 and σ2Y = 3, find the variance of the random variable Z = −2X + 4Y − 3.
> Use Theorem 4.7 to evaluate E(2XY2 − X2Y ) for the joint probability distribution shown in Table 3.1 on page 96.
> Suppose that X and Y are independent random variables having the joint probability distribution Find (a) E(2X − 3Y ); (b) E(XY ). f(x, y) 4 0.10 0.15 3 0.20 1 0.30 0.10 0.15
> An attendant at a car wash is paid according to the number of cars that pass through. Suppose the probabilities are 1/12, 1/12, 1/4, 1/4, 1/6, and 1/6, respectively, that the attendant receives $7, $9, $11, $13, $15, or $17 between 4:00 P.M. and 5:00 P.M
> If a random variable X is defined such that E[(X − 1)2] = 10 and E[(X − 2)2 ]=6, find μ and σ2.
> The total time, measured in units of 100 hours, that a teenager runs her hair dryer over a period of one year is a continuous random variable X that has the density function Use Theorem 4.6 to evaluate the mean of the random variable Y = 60X2 + 39X, wh
> Let X be a random variable with the following probability distribution: Find E(X) and E(X2) and then, using these values, evaluate E[(2X + 1)2]. -3 6 9 f (x) 6 3
> Repeat Exercise 4.43 on page 127 by applying Theorem 4.5 and Corollary 4.6. Exercise 4.43: The length of time, in minutes, for an airplane to obtain clearance for takeoff at a certain airport is a random variable Y = 3X −2, where X has
> Suppose that a grocery store purchases 5 cartons of skim milk at the wholesale price of $1.20 per carton and retails the milk at $1.65 per carton. After the expiration date, the unsold milk is removed from the shelf and the grocer receives a credit from
> Using Theorem 4.5 and Corollary 4.6, find the mean and variance of the random variable Z = 5X + 3, where X has the probability distribution of Exercise 4.36 on page 127. Exercise 4.36: Suppose that the probabilities are 0.4, 0.3, 0.2, and 0.1, respectiv
> An annexation suit against a county subdivision of 1200 residences is being considered by a neighboring city. If the occupants of half the residences object to being annexed, what is the probability that in a random sample of 10 at least 3 favor the anne
> Random variables X and Y follow a joint distribution Determine the correlation coefficient between X and Y . (2, 0 <x <y < 1, 0, otherwise. f (x, y) =
> For the random variables X and Y in Exercise 3.39 on page 105, determine the correlation coefficient between X and Y . Exercise 3.39: From a sack of fruit containing 3 oranges, 2 apples, and 3 bananas, a random sample of 4 pieces of fruit is selected. I
> For a laboratory assignment, if the equipment is working, the density function of the observed outcome X is Find the variance and standard deviation of X. 2(1 — 2), 0 <х<1, (0, f (x) = otherwise.
> In a gambling game, a woman is paid $3 if she draws a jack or a queen and $5 if she draws a king or an ace from an ordinary deck of 52 playing cards. If she draws any other card, she loses. How much should she pay to play if the game is fair?
> Consider the situation in Exercise 4.32 on page 119. The distribution of the number of imperfections per 10 meters of synthetic failure is given by Find the variance and standard deviation of the number of imperfections. 1 3 4 f(x) 0.41 0.37 0.16 0
> Given a random variable X, with standard deviation σX, and a random variable Y = a + bX, show that if b < 0, the correlation coefficient ρXY = −1, and if b > 0, ρXY = 1.
> For the random variables X and Y whose joint density function is given in Exercise 3.40 on page 105, find the covariance.
> Find the covariance of the random variables X and Y of Exercise 3.44 on page 105.
> Find the covariance of the random variables X and Y of Exercise 3.49 on page 106.
> Among 150 IRS employees in a large city, only 30 are women. If 10 of the employees are chosen at random to provide free tax assistance for the residents of this city, use the binomial approximation to the hypergeometric distribution to find the probabili
> Find the covariance of the random variables X and Y of Exercise 3.39 on page 105.
> The length of time, in minutes, for an airplane to obtain clearance for takeoff at a certain airport is a random variable Y = 3X −2, where X has the density function Find the mean and variance of the random variable Y . Sie-/4, x
> Using the results of Exercise 4.21 on page 118, find the variance of g(X) = X2, where X is a random variable having the density function given in Exercise 4.12 on page 117.
> Find the standard deviation of the random variable g(X) = (2X + 1)2 in Exercise 4.17 on page 118.
> Referring to Exercise 4.14 on page 117, find σ2(X) for the function g(X)=3X2 + 4.
> A coin is biased such that a head is three times as likely to occur as a tail. Find the expected number of tails when this coin is tossed twice.
> The total number of hours, in units of 100 hours, that a family runs a vacuum cleaner over a period of one year is a random variable X having the density function given in Exercise 4.13 on page 117. Find the variance of X.
> The proportion of people who respond to a certain mail-order solicitation is a random variable X having the density function given in Exercise 4.14 on page 117. Find the variance of X.
> A dealer’s profit, in units of $5000, on a new automobile is a random variable X having the density function given in Exercise 4.12 on page 117. Find the variance of X.
> Suppose that the probabilities are 0.4, 0.3, 0.2, and 0.1, respectively, that 0, 1, 2, or 3 power failures will strike a certain subdivision in any given year. Find the mean and variance of the random variable X representing the number of power failures
> Suppose that the manufacturing company of Exercise 5.36 decides to change its acceptance scheme. Under the new scheme, an inspector takes 1 item at random, inspects it, and then replaces it in the box; a second inspector does likewise. Finally, a third i
> The random variable X, representing the number of errors per 100 lines of software code, has the following probability distribution: Using Theorem 4.2 on page 121, find the variance of X. 2 3 4 5 f(x) | 0.01 0.25 0.4 0.3 0.04
> Let X be a random variable with the following probability distribution: Find the standard deviation of X. -2 3 5 f(x) 0.3 0.2 0.5
> Use Definition 4.3 on page 120 to find the variance of the random variable X of Exercise 4.7 on page 117.
> In Exercise 3.13 on page 92, the distribution of the number of imperfections per 10 meters of synthetic fabric is given by (a) Plot the probability function. (b) Find the expected number of imperfections, E(X) = μ. (c) Find E(X2). 1 2
> Consider Exercise 3.32 on page 94. (a) What is the mean proportion of the budget allocated to environmental and pollution control? (b) What is the probability that a company selected at random will have allocated to environmental and pollution control a
> In Exercise 3.31 on page 94, the distribution of times before a major repair of a washing machine was given as What is the population mean of the times to repair? Sie-v/4, y 2 0, f(y) : (0, elsewhere.
> Find the mean of the random variable T representing the total of the three coins in Exercise 3.25 on page 93.
> Exercise 3.29 on page 93 dealt with an important particle size distribution characterized by (a) Plot the density function. (b) Give the mean particle size. -4 f(x) = S3x¯ x > 1, elsewhere.
> Consider the information in Exercise 3.28 on page 93. The problem deals with the weight in ounces of the product in a cereal box, with (a) Plot the density function. (b) Compute the expected value, or mean weight, in ounces. (c) Are you surprised at yo
> In Exercise 3.27 on page 93, a density function is given for the time to failure of an important component of a DVD player. Find the mean number of hours to failure of the component and thus the DVD player.
> A manufacturing company uses an acceptance scheme on items from a production line before they are shipped. The plan is a two-stage one. Boxes of 25 items are readied for shipment, and a sample of 3 items is tested for defectives. If any defectives are fo
> Referring to the random variables whose joint probability distribution is given in Exercise 3.51 on page 106, find the mean for the total number of jacks and kings when 3 cards are drawn without replacement from the 12 face cards of an ordinary deck of 5
> Referring to the random variables whose joint probability distribution is given in Exercise 3.39 on page 105, (a) find E(X2Y − 2XY ); (b) find μX − μY .
> Suppose that X and Y have the following joint probability function: (a) Find the expected value of g(X, Y ) = XY2. (b) Find μX and μY . f(x, y) 4 1 0.10 0.15 3 0.20 0.30 0.10 0.15
> The hospitalization period, in days, for patients following treatment for a certain type of kidney disorder is a random variable Y = X + 4, where X has the density function Find the average number of days that a person is hospitalized following treatme
> What is the dealer’s average profit per automobile if the profit on each automobile is given by g(X) = X2, where X is a random variable having the density function of Exercise 4.12?
> A continuous random variable X has the density function Find the expected value of g(X) = e2X/3. x > 0, 0, f (x) : elsewhere.
> The probability distribution of the discrete random variable X is Find the mean of X. 3-r 3 3 f (x) : x = 0,1,2, 3. 4
> A large industrial firm purchases several new word processors at the end of each year, the exact number depending on the frequency of repairs in the previous year. Suppose that the number of word processors, X, purchased each year has the following proba
> Find the expected value of the random variable g(X) = X2, where X has the probability distribution of Exercise 4.2.
> A company is interested in evaluating its current inspection procedure for shipments of 50 identical items. The procedure is to take a sample of 5 and pass the shipment if no more than 2 are found to be defective. What proportion of shipments with 20% de
> Let X be a random variable with the following probability distribution: Find μg(X), where g(X) = (2X + 1)2. -3 6 9 f (x) 1/6 1/2 1/3
> Suppose that you are inspecting a lot of 1000 light bulbs, among which 20 are defectives. You choose two light bulbs randomly from the lot without replacement. Let Find the probability that at least one light bulb chosen is defective. 1, if the 1st
> Assume that two random variables (X, Y) are uniformly distributed on a circle with radius a. Then the joint probability density function is Find μX, the expected value of X. S , a? +y? < a?, f(x, y) 10, otherwise.
> Find the proportion X of individuals who can be expected to respond to a certain mail-order solicitation if X has the density function 2(x+2) 0 < x < 1, f (x) = 0, elsewhere.
> The density function of the continuous random variable X, the total number of hours, in units of 100 hours, that a family runs a vacuum cleaner over a period of one year, is given in Exercise 3.7 on page 92 as Find the average number of hours per year
> If a dealer’s profit, in units of $5000, on a new automobile can be looked upon as a random variable X having the density function find the average profit per automobile. S 2(1 – x), 0<< x < 1, (0, f(x) = elsewhere,
> The density function of coded measurements of the pitch diameter of threads of a fitting is Find the expected value of X. 4 0 < x < 1, f (x) = T(1+x²)' 0, elsewhere.
> Consider Review Exercise 3.73 on page 108. It involved Y, the proportion of impurities in a batch, and the density function is given by (a) Find the expected percentage of impurities. (b) Find the expected value of the proportion of quality material (i
> As we shall illustrate in Chapter 12, statistical methods associated with linear and nonlinear models are very important. In fact, exponential functions are often used in a wide variety of scientific and engineering problems. Consider a model that is fit

