Question: Let X1 and X2 be discrete random
Let X1 and X2 be discrete random variables with the joint multinomial distribution
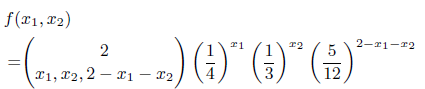
for x1 = 0, 1, 2; x2 = 0, 1, 2; x1 + x2 ≤ 2; and zero elsewhere. Find the joint probability distribution of
Y1 = X1 + X2 and Y2 = X1 − X2.
Transcribed Image Text:
f(T1, x2) 2-r1-12 5 ()" r2 2 T1, 12, 2 – xi – x2 3 12 ||
> A technician plans to test a certain type of resin developed in the laboratory to determine the nature of the time required before bonding takes place. It is known that the mean time to bonding is 3 hours and the standard deviation is 0.5 hour. It will b
> A controlled satellite is known to have an error (distance from target) that is normally distributed with mean zero and standard deviation 4 feet. The manufacturer of the satellite defines a success as a firing in which the satellite comes within 10 feet
> The speed of a molecule in a uniform gas at equilibrium is a random variable V whose probability distribution is given by where k is an appropriate constant and b depends on the absolute temperature and mass of the molecule. Find the probability distri
> The elongation of a steel bar under a particular load has been established to be normally distributed with a mean of 0.05 inch and σ = 0.01 inch. Find the probability that the elongation is (a) above 0.1 inch; (b) below 0.04 inch; (c) between 0.025 and 0
> For an electrical component with a failure rate of once every 5 hours, it is important to consider the time that it takes for 2 components to fail. (a) Assuming that the gamma distribution applies, what is the mean time that it takes for 2 components to
> In a chemical processing plant, it is important that the yield of a certain type of batch product stay above 80%. If it stays below 80% for an extended period of time, the company loses money. Occasional defective batches are of little concern. But if se
> A certain type of device has an advertised failure rate of 0.01 per hour. The failure rate is constant and the exponential distribution applies. (a) What is the mean time to failure? (b) What is the probability that 200 hours will pass before a failure i
> According to a recent census, almost 65% of all households in the United States were composed of only one or two persons. Assuming that this percentage is still valid today, what is the probability that between 590 and 625, inclusive, of the next 1000 ra
> Consider Exercise 9.9. Compute a 95% prediction interval for the sugar content of the next single serving of Alpha-Bits. Exercise 9.9 Regular consumption of presweetened cereals contributes to tooth decay, heart disease, and other degenerative diseases,
> A manufacturer of a certain type of large machine wishes to buy rivets from one of two manufacturers. It is important that the breaking strength of each rivet exceed 10,000 psi. Two manufacturers (A and B) offer this type of rivet and both have rivets wh
> When α is a positive integer n, the gamma distribution is also known as the Erlang distribution. Setting α = n in the gamma distribution on page 195, the Erlang distribution is It can be shown that if the times between succe
> The exponential distribution is frequently applied to the waiting times between successes in a Poisson process. If the number of calls received per hour by a telephone answering service is a Poisson random variable with parameter λ = 6, we know that the
> According to a study published by a group of sociologists at the University of Massachusetts, approximately 49% of the Valium users in the state of Massachusetts are white-collar workers. What is the probability that between 482 and 510, inclusive, of th
> Show that the failure-rate function is given by Z(t) = αβ tβ−1, t>0, if and only if the time to failure distribution is the Weibull distribution f(t) = αβ tβ−1 e–αtβ, t>0.
> Given the random variable X with probability distribution find the probability distribution of Y = 8X3. S2.x, 0<x < 1, f(x) = 10, elsewhere,
> Consider the information in Exercise 6.58. (a) What is the probability that more than 1 minute elapses between arrivals? (b) What is the mean number of minutes that elapse between arrivals? Exercise 6.58: The number of automobiles that arrive at a certa
> The number of automobiles that arrive at a certain intersection per minute has a Poisson distribution with a mean of 5. Interest centers around the time that elapses before 10 automobiles appear at the intersection. (a) What is the probability that more
> For Exercise 6.56, what is the mean power usage (average dB per hour)? What is the variance? Exercise 6.56: Rate data often follow a lognormal distribution. Average power usage (dB per hour) for a particular company is studied and is known to have a log
> Rate data often follow a lognormal distribution. Average power usage (dB per hour) for a particular company is studied and is known to have a lognormal distribution with parameters μ = 4 and σ = 2. What is the probability that the company uses more than
> Consider Exercise 9.10. Compute the 95% prediction interval for the next observed number of words per minute typed by a graduate of the secretarial school. Exercise 9.10: A random sample of 12 graduates of a certain secretarial school typed an average o
> The lifetime, in weeks, of a certain type of transistor is known to follow a gamma distribution with mean 10 weeks and standard deviation √50 weeks. (a) What is the probability that a transistor of this type will last at most 50 weeks? (b) What is the pr
> In a biomedical research study, it was determined that the survival time, in weeks, of an animal subjected to a certain exposure of gamma radiation has a gamma distribution with α = 5 and β = 10. (a) What is the mean survival time of a randomly selected
> Derive the mean and variance of the Weibull distribution.
> The lives of a certain automobile seal have the Weibull distribution with failure rate Z(t) =1/√t. Find the probability that such a seal is still intact after 4 years.
> If the proportion of a brand of television set requiring service during the first year of operation is a random variable having a beta distribution with α = 3 and β = 2, what is the probability that at least 80% of the new models of this brand sold this
> Let X have the probability distribution Show that the random variable Y = −2 lnX has a chisquared distribution with 2 degrees of freedom. S1, 0< x < 1, 10, elsewhere. f(x)
> Suppose the random variable X follows a beta distribution with α = 1 and β = 3. (a) Determine the mean and median of X. (b) Determine the variance of X. (c) Find the probability that X >1/3.
> Derive the mean and variance of the beta distribution.
> Suppose that the service life, in years, of a hearing aid battery is a random variable having a Weibull distribution with α = 1/2 and β = 2. (a) How long can such a battery be expected to last? (b) What is the probability that such a battery will be oper
> The life, in years, of a certain type of electrical switch has an exponential distribution with an average life β = 2. If 100 of these switches are installed in different systems, what is the probability that at most 30 fail during the first year?
> Referring to Exercise 9.5, construct a 99% prediction interval for the kilometers traveled annually by an automobile owner in Virginia. Exercise 9.5 A random sample of 100 automobile owners in the state of Virginia shows that an automobile is driven on
> The length of time for one individual to be served at a cafeteria is a random variable having an exponential distribution with a mean of 4 minutes. What is the probability that a person is served in less than 3 minutes on at least 4 of the next 6 days?
> In a certain city, the daily consumption of electric power, in millions of kilowatt-hours, is a random variable X having a gamma distribution with mean μ = 6 and variance σ2 = 12. (a) Find the values of α and β. (b) Find the probability that on any given
> (a) Find the mean and variance of the daily water consumption in Exercise 6.40. (b) According to Chebyshev’s theorem, there is a probability of at least 3/4 that the water consumption on any given day will fall within what interval?
> Suppose that the time, in hours, required to repair a heat pump is a random variable X having a gamma distribution with parameters α = 2 and β = 1/2. What is the probability that on the next service call (a) at most 1 hour will be required to repair the
> If a random variable X has the gamma distribution with α = 2 and β = 1, find P(1.8 < X < 2.4).
> In a certain city, the daily consumption of water (in millions of liters) follows approximately a gamma distribution with α = 2 and β = 3. If the daily capacity of that city is 9 million liters of water, what is the probability that on any given day the
> Let X1 and X2 be discrete random variables with joint probability distribution Find the probability distribution of the random variable Y = X1X2. xi = 1,2; x2 = 1, 2, 3, f (71, x2) = 18, 10, elsewhere.
> Use the gamma function with y =√2x to show that Γ(1/2) =√π.
> A telemarketing company has a special letter opening machine that opens and removes the contents of an envelope. If the envelope is fed improperly into the machine, the contents of the envelope may not be removed or may be damaged. In this case, the mach
> The serum cholesterol level X in 14-year-old boys has approximately a normal distribution with mean 170 and standard deviation 30. (a) Find the probability that the serum cholesterol level of a randomly chosen 14-year-old boy exceeds 230. (b) In a middle
> The following measurements were recorded for the drying time, in hours, of a certain brand of latex paint: Assuming that the measurements represent a random sample from a normal population, find a 95% prediction interval for the drying time for the nex
> A common practice of airline companies is to sell more tickets for a particular flight than there are seats on the plane, because customers who buy tickets do not always show up for the flight. Suppose that the percentage of no-shows at flight time is 2%
> A company produces component parts for an engine. Parts specifications suggest that 95% of items meet specifications. The parts are shipped to customers in lots of 100. (a) What is the probability that more than 2 items in a given lot will be defective?
> A pair of dice is rolled 180 times. What is the probability that a total of 7 occurs (a) at least 25 times? (b) between 33 and 41 times inclusive? (c) exactly 30 times?
> Statistics released by the National Highway Traffic Safety Administration and the National Safety Council show that on an average weekend night, 1 out of every 10 drivers on the road is drunk. If 400 drivers are randomly checked next Saturday night, what
> A pharmaceutical company knows that approximately 5% of its birth-control pills have an ingredient that is below the minimum strength, thus rendering the pill ineffective. What is the probability that fewer than 10 in a sample of 200 pills will be ineffe
> One-sixth of the male freshmen entering a large state school are out-of-state students. If the students are assigned at random to dormitories, 180 to a building, what is the probability that in a given dormitory at least one-fifth of the students are fro
> A drug manufacturer claims that a certain drug cures a blood disease, on the average, 80% of the time. To check the claim, government testers use the drug on a sample of 100 individuals and decide to accept the claim if 75 or more are cured. (a) What is
> If 20% of the residents in a U.S. city prefer a white telephone over any other color available, what is the probability that among the next 1000 telephones installed in that city (a) between 170 and 185 inclusive will be white? (b) at least 210 but not m
> Researchers at George Washington University and the National Institutes of Health claim that approximately 75% of people believe “tranquilizers work very well to make a person more calm and relaxed.” Of the next 80 people interviewed, what is the probabi
> A random sample of 12 shearing pins is taken in a study of the Rockwell hardness of the pin head. Measurements on the Rockwell hardness are made for each of the 12, yielding an average value of 48.50 with a sample standard deviation of 1.5. Assuming the
> The probability that a patient recovers from a delicate heart operation is 0.9. Of the next 100 patients having this operation, what is the probability that (a) between 84 and 95 inclusive survive? (b) fewer than 86 survive?
> A process yields 10% defective items. If 100 items are randomly selected from the process, what is the probability that the number of defectives (a) exceeds 13? (b) is less than 8?
> A process for manufacturing an electronic component yields items of which 1% are defective. A quality control plan is to select 100 items from the process, and if none are defective, the process continues. Use the normal approximation to the binomial to
> A coin is tossed 400 times. Use the normal curve approximation to find the probability of obtaining (a) between 185 and 210 heads inclusive; (b) exactly 205 heads; (c) fewer than 176 or more than 227 heads.
> If both X and Y, distributed independently, follow exponential distributions with mean parameter 1, find the distributions of (a) U = X + Y; (b) V = X/(X + Y ).
> Using the moment-generating function of Exercise 7.21, show that the mean and variance of the chisquared distribution with v degrees of freedom are, respectively, v and 2v. Exercise 7.21: Show that the moment-generating function of the random variable X
> Show that the moment-generating function of the random variable X having a chi-squared distribution with v degrees of freedom is MX(t) = (1 − 2t) −v/2.
> The moment-generating function of a certain Poisson random variable X is given by MX(t) = e4(et−1). Find P(μ − 2σ
> Let X be a binomial random variable with probability distribution Find the probability distribution of the random variable Y = X2. 3-r x = 0, 1, 2, 3, f(r) = 0, elsewhere.
> A random variable X has the Poisson distribution p(x; μ) = e −μμx/x! for x = 0, 1, 2, . . . . Show that the moment-generating function of X is MX(t) = eμ(et−1). Using MX(t), find the mean and variance of the Poisson distribution.
> A random sample of 10 chocolate energy bars of a certain brand has, on average, 230 calories per bar, with a standard deviation of 15 calories. Construct a 99% confidence interval for the true mean calorie content of this brand of energy bar. Assume that
> A random variable X has the geometric distribution g(x; p) = pqx−1 for x = 1, 2, 3, . . . . Show that the moment-generating function of X is and then use MX(t) to find the mean and variance of the geometric distribution. pet 1- qe
> A random variable X has the discrete uniform distribution Show that the moment-generating function of X is SE r = 1,2, ..., k, 0, elsewhere. f (x; k) = e'(1 – ekt) k(1 – et) Mx (t) =
> Show that the rth moment about the origin of the gamma distribution is B"T(a + r) T(a)
> Let X have the probability distribution Find the probability distribution of the random variable Y = X2. 2(x+1). -1< x < 2, f(x) = elsewhere.
> Let X be a random variable with probability distribution Find the probability distribution of the random variable Y = X2. S, -1< x < 1, 10, 1+z f(r) = elsewhere.
> A current of I amperes flowing through a resistance of R ohms varies according to the probability distribution If the resistance varies independently of the current according to the probability distribution find the probability distribution for the p
> A certain supplier manufactures a type of rubber mat that is sold to automotive companies. The material used to produce the mats must have certain hardness characteristics. Defective mats are occasionally discovered and rejected. The supplier claims that
> A group of human factor researchers are concerned about reaction to a stimulus by airplane pilots in a certain cockpit arrangement. An experiment was conducted in a simulation laboratory, and 15 pilots were used with average reaction time of 3.2 seconds
> Consider the statistic S2 p, the pooled estimate of σ2 discussed in Section 9.8. It is used when one is willing to assume that σ2 1 = σ22 = σ2. Show that the estimator is unbiased for σ2 [i.e., show that E(S2p) = σ2]. You may make use of results from any
> A consumer group is interested in comparing operating costs for two different types of automobile engines. The group is able to find 15 owners whose cars have engine type A and 15 whose cars have engine type B. All 30 owners bought their cars at roughly
> A machine produces metal pieces that are cylindrical in shape. A sample of pieces is taken, and the diameters are found to be 1.01, 0.97, 1.03, 1.04, 0.99, 0.98, 0.99, 1.01, and 1.03 centimeters. Find a 99% confidence interval for the mean diameter of pi
> A machine is used to fill boxes with product in an assembly line operation. Much concern centers around the variability in the number of ounces of product in a box. The standard deviation in weight of product is known to be 0.3 ounce. An improvement is i
> A manufacturer turns out a product item that is labeled either “defective” or “not defective.” In order to estimate the proportion defective, a random sample of 100 items is taken from production, and 10 are found to be defective. Following implementatio
> Refer to Review Exercise 9.106. Suppose there is concern about whether the point estimate ˆp = 8/30 is accurate enough because the confidence interval around p is not sufficiently narrow. Using ˆp as the estimate of p, how many companies would need to be
> A random sample of 30 firms dealing in wireless products was selected to determine the proportion of such firms that have implemented new software to improve productivity. It turned out that 8 of the 30 had implemented such software. Find a 95% confidenc
> A labor union is becoming defensive about gross absenteeism by its members. The union leaders had always claimed that, in a typical month, 95% of its members were absent less than 10 hours. The union decided to check this by monitoring a random sample of
> Consider Review Exercise 9.103. Let us assume that the data have not been collected yet and that previous statistics suggest that σ1 = σ2 = $4000. Are the sample sizes in Review Exercise 9.103 sufficient to produce a 95% confidence interval on μ1 −μ2 hav
> A survey was done with the hope of comparing salaries of chemical plant managers employed in two areas of the country, the northern and west central regions. An independent random sample of 300 plant managers was selected from each of the two regions. Th
> Specify the moment estimators for α and β for the gamma distribution.
> Specify the moment estimators for μ and σ2 for the lognormal distribution.
> Specify the moment estimators for μ and σ2 for the normal distribution.
> A random sample of 12 graduates of a certain secretarial school typed an average of 79.3 words per minute with a standard deviation of 7.8 words per minute. Assuming a normal distribution for the number of words typed per minute, find a 95% confidence in
> A UCLA researcher claims that the life span of mice can be extended by as much as 25% when the calories in their diet are reduced by approximately 40% from the time they are weaned. The restricted diet is enriched to normal levels by vitamins and protein
> Go back to Review Exercise 5.95(a). Recompute the probability using the binomial distribution. Comment.
> Suppose it is important that the overall missile defense system be as near perfect as possible. (a) Assuming the quality of the screens is as indicated in Review Exercise 5.97, how many are needed to ensure that the probability that a missile gets throug
> National security requires that defense technology be able to detect incoming projectiles or missiles. To make the defense system successful, multiple radar screens are required. Suppose that three independent screens are to be operated and the probabili
> Consider the situation of Review Exercise 5.95. It has been determined that the sampling plan should be extensive enough that there is a high probability, say 0.9, that if as many as 2 defectives exist in the lot of 50 being sampled, at least 1 will be f
> A production process outputs items in lots of 50. Sampling plans exist in which lots are pulled aside periodically and exposed to a certain type of inspection. It is usually assumed that the proportion defective is very small. It is important to the comp
> A production process produces electronic component parts. It is presumed that the probability of a defective part is 0.01. During a test of this presumption, 500 parts are sampled randomly and 15 defectives re observed. (a) What is your response to the p
> It is known by researchers that 1 in 100 people carries a gene that leads to the inheritance of a certain chronic disease. In a random sample of 1000 individuals, what is the probability that fewer than 7 individuals carry the gene? Use a Poisson approxi
> A couple decides to continue to have children until they have two males. Assuming that P(male) = 0.5, what is the probability that their second male is their fourth child?
> Consider the information in Review Exercise 5.90. The drilling company feels that it will “hit it big” if the second success occurs on or before the sixth attempt. What is the probability that the driller will hit it big? Exercise 5.90: An oil drilling
> An oil drilling company ventures into various locations, and its success or failure is independent from one location to another. Suppose the probability of a success at any specific location is 0.25. (a) What is the probability that the driller drills at
> In testing a certain kind of truck tire over rugged terrain, it is found that 25% of the trucks fail to complete the test run without a blowout. Of the next 15 trucks tested, find the probability that (a) from 3 to 6 have blowouts; (b) fewer than 4 have
> The acceptance scheme for purchasing lots containing a large number of batteries is to test no more than 75 randomly selected batteries and to reject a lot if a single battery fails. Suppose the probability of a failure is 0.001. (a) What is the probabil
> The potential buyer of a particular engine requires (among other things) that the engine start successfully 10 consecutive times. Suppose the probability of a successful start is 0.990. Let us assume that the outcomes of attempted starts are independent.
> Imperfections in computer circuit boards and computer chips lend themselves to statistical treatment. For a particular type of board, the probability of a diode failure is 0.03 and the board contains 200 diodes. (a) What is the mean number of failures am

