Question: Make a substitution to express the integrand
Make a substitution to express the integrand as a rational function and then evaluate the integral.
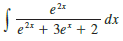
Transcribed Image Text:
dx e2* + 3e* + 2
> Use a graphing device to graph the polar curve. Choose the parameter interval carefully to make sure that you produce an appropriate curve. r = | tan e |lcot el (valentine curve)
> Sketch the curve with the given polar equation. r = sin θ
> Sketch the curve with the given polar equation. r2 – 3r + 2 = 0
> Sketch the curve with the given polar equation. θ = -π/6
> For each of the described curves, decide if the curve would be more easily given by a polar equation or a Cartesian equation. Then write an equation for the curve. (a). A circle with radius 5 and center (2, 2) (b). A circle centered at the origin with ra
> For each of the described curves, decide if the curve would be more easily given by a polar equation or a Cartesian equation. Then write an equation for the curve. (a). A line through the origin that makes an angle of π/6 with the positive x-axis (b). A
> Find a polar equation for the curve represented by the given Cartesian equation. xy = 4
> Plot the point whose polar coordinates are given. Then find two other pairs of polar coordinates of this point, one with r > 0 and one with r (а) (1, 7п/4) (b) (-3, п/6) (с) (1, — 1)
> Find a polar equation for the curve represented by the given Cartesian equation. x2 + y2 = 2cx
> Find a polar equation for the curve represented by the given Cartesian equation. x + y = 9
> Find a polar equation for the curve represented by the given Cartesian equation. x = -y2
> Use a graphing device to graph the polar curve. Choose the parameter interval carefully to make sure that you produce an appropriate curve. r= esin e – 2 cos(40) (butterfly curve)
> Identify the curve by finding a Cartesian equation for the curve. r = tan 0 sec e
> Identify the curve by finding a Cartesian equation for the curve. r = csc e
> Identify the curve by finding a Cartesian equation for the curve. r= 2 sin e + 2 cos e
> Evaluate the integral. f ax/x2 – bx, dx
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. r> 1, 7<es 27
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. 2 <r< 3, 57/3 < 0 < 7m/3
> Plot the point whose polar coordinates are given. Then find two other pairs of polar coordinates of this point, one with r > 0 and one with r (а) (2, т/3) (b) (1, — Зӕ/4) (с) (-1, п/2)
> Write the sum in expanded form. ∑n-1j=0 (-i)j
> Evaluate the integral. f r2/r + 4, dr
> Solve the inequality in terms of intervals and illustrate the solution set on the real number line. x' + 3x < 4x?
> Show that the curves r = a sin θ and r = a cos θ intersect at right angles.
> Evaluate the integral. f x/x – 6, dx
> Solve the inequality in terms of intervals and illustrate the solution set on the real number line. x3 > x
> Solve the inequality in terms of intervals and illustrate the solution set on the real number line. x2 < 3
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. (a) (r' + x)(x? – x + 3) 1 (b) x° - x .3
> Solve the inequality in terms of intervals and illustrate the solution set on the real number line. 4 — Зх в 6
> Solve the inequality in terms of intervals and illustrate the solution set on the real number line. 2x + 7>3
> Let P (x1, y1) be a point on the ellipse x2/a2 + y2/b2 = 1 with foci F1 and F2 and let α and β be the angles between the lines PF1, PF2 and the ellipse as shown in the figure. Prove that α = β. This exp
> Sketch the region bounded by the curves. y = 4 – x2 and x – 2y = 2
> Sketch the region bounded by the curves. x + 4y = 8 and x = 2y2 - 8
> (a). Find the foci and asymptotes of the hyperbola x2 – y2 = 1 and sketch its graph. (b). Sketch the graph of y2 – x2 = 1.
> Suppose that P (x, y) is any point on the parabola with focus (0, p) and directrix y = -p. (See Figure 14 (below).) Use the definition of a parabola to show that x2 = 4py. P(x, y) F(0, p) y y=-p
> Use the definition of a hyperbola to derive Equation 2 for a hyperbola with foci (±c, 0).
> Evaluate ∑ni-1 [ ∑nj-1 (i + j).
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. t* + t? + 1 (a) x* - 1 (b) (t2 + 1)(1? + 4)?
> Evaluate ∑ni-1 (2i + 2i).
> Find the limit. limn→∞ ∑n i=1 3/n [ (1 + 3i/n)3 - 2 (1 + 3i/n)]
> Find the limit. limn→∞ ∑n i=1 2/n [ (2i/n)3 + 5 (2i/n)]
> Find the limit. limn→∞ ∑n i=1 1/n [ (i/n)3 + 1]
> Find the limit. limn→∞ ∑n i=1 1/n (i/n)2
> The region under the curve y = 1/x2 + 3x + 2 from x = 0 to x = 1 is rotated about the x-axis. Find the volume of the resulting solid.
> One method of slowing the growth of an insect population without using pesticides is to introduce into the population a number of sterile males that mate with fertile females but produce no offspring. If represents the number of female insects in a popul
> (a). Show that the area of a triangle with sides of lengths a and b and with included angle θ is A = 1/2 ab sin θ (b). Find the area of triangle ABC, correct to five decimal places, if |AB| = 10 cm | BC| = 3 cm ZABC 107°
> Graph both y = 1/ (x3 – 2x2) and an antiderivative on the same screen.
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. 2x + 1 (a) x? + 4x + 3 (b) (x + 1)°(x² + 4)²
> Use a graph of f (x) = 1/ (x2 – 2x – 3) to decide whether f20 f (x) dx is positive or negative. Use the graph to give a rough estimate of the value of the integral and then use partial fractions to find the exact value.
> Make a substitution to express the integrand as a rational function and then evaluate the integral. cos x dx sin'x + sin x sin*x
> Make a substitution to express the integrand as a rational function and then evaluate the integral. dx 2/x + 3 + x
> Make a substitution to express the integrand as a rational function and then evaluate the integral. x, dx J9 x- 4 16
> Evaluate the integral. f 3x2 + x + 4/ x4 + 3x2 + 2, dx
> Evaluate the integral. f x – 3/ (x2 + 2x + 4)2, dx
> Evaluate the integral. f x4 + 3x2 + 1/x5 + 5x3 + 5x, dx
> (a). If is a complex-valued function of a real variable, its indefinite integral f u (x) dx is an antiderivative of u. Evaluate (b). By considering the real and imaginary parts of the integral in part (a), evaluate the real integrals (c). Compare wit
> Evaluate the integral. f dx/x (x2 + 4)2
> Evaluate the integral. f x3/x3 + 1, dx
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. x* + 1 (a) x* + 4x 1 (b) (x² – 9)²
> Evaluate the integral. f 1/x3 – 1, dx
> Evaluate the integral. f10 x/x2 + 4x + 13, dx
> Evaluate the integral. f x + 4/x2 + 2x + 5, dx
> Evaluate the integral. f x2 + x + 1/ (x2 + 1)2, dx
> Evaluate the integral. f x3 + x2 + 2x + 1/ (x2 + 1) (x2 + 2), dx
> Evaluate the integral. f x2 – 2x – 1/ (x – 1)2 (x2 + 1), dx
> Evaluate the integral. f 10/ (x – 1) (x2 + 9), dx
> Suppose an ellipse has foci (±c, 0) and the sum of the distances from any point P (x, y) on the ellipse to the foci is 2a. Show that the coordinates of P satisfy Equation 1.
> Use the given graph of f (x) = √x to find a number δ such that if |x – 4|< 8 |V - 2|<0.4 then y4 y= Va 2.4. 2 1.6 4
> Evaluate the integral. f x2 – x + 6/x3 + 3x, dx
> Evaluate the integral. f 5x2 + 3x – 2/x3 + 2x2, dx
> Evaluate the integral. f x2 – 5x + 16/(2x + 1) (x – 2)2 dx
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. x? (a) x? + x – 2 (b) x? + x + 2
> Evaluate the integral. f 1/(x + 5)2 (x – 1), dx
> Evaluate the integral. f x2 + 2x – 1/x3 – x, dx
> Evaluate the integral. f11 4y2 – 7y -12/y (y + 2) (y – 3), dy
> Evaluate the integral. f10 x3 – 4x – 10/x2 – x – 6, dx
> Evaluate the integral. f43 x3 – 2x2 - 4/x3 – 2x2, dx
> Evaluate the integral. f 1/(x + a) (x + b), dx
> Match the polar equations with the graphs labeled I–VI. Give reasons for your choices. (Don’t use a graphing device.) I II III IV V VI (a) r = Ve, 0<0 < 167 (b) r= 0², 0< 0< 167 (c) r= cos(0/3) (e) r = 2 + sin 30
> Evaluate the integral. f10 x - 1/x2 + 3x + 2, dx
> Evaluate the integral. f32 1/x2 – 1, dx
> Evaluate the integral. f 1/(t – 4) (t – 1), dt
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. 2x 1 (a) (x + 3)(3x + 1) (b) x + 2x? + x
> Write the sum in expanded form. ∑n+3j=n j2
> Write the sum in expanded form. ∑ni=1 i10
> Write the sum in expanded form. ∑8k=5 xk
> Write the sum in expanded form. ∑4k=1 2k – 1/ 2k + 1
> Prove the generalized triangle inequality: |∑ n i=1 ai| < ∑n i=1 |ai|
> Evaluate each telescoping sum. (a). ∑n i=1 [i4 – (i – 1)4] 100 (b) E (5' – 5i-1) i- 99 (c) Σ (d) Σ (a, - a-1) i+1 i-3 i-l
> (a). In Example 11 the graphs suggest that the limaçon r = 1 + c sin θ has an inner loop when |c| > 1. Prove that this is true, and find the values of θ that correspond to the inner loop. (b). From Figure 19 it a
> Prove formula (e) of Theorem 3 using the following method published by Abu Bekr Mohammed ibn Alhusain Alkarchi in about AD 1010. The figure shows a square ABCD in which sides AB and AD have been divided into segments of lengths ,1, 2, . . . n, Thus the s
> Write the sum in expanded form. ∑6i=4 i3
> Prove formula (e) of Theorem 3 using a method similar to that of Example 5, Solution 1 [start with (1 + i)4 – i4].
> Prove formula (e) of Theorem 3 using mathematical induction.
> Prove formula (b) of Theorem 3.
> Find the number n such that ∑n i=1 i = 78.
> Find the value of the sum. ∑ni=1 (t3 – i - 2)
> Find the value of the sum. ∑ni=1 (i + 1) (i + 2)
> Find the value of the sum. ∑ni=1 (i + 1) (i + 2)
> Find the value of the sum. ∑ni=1 (3 + 2i)2
> If f is a quadratic function such that f (0) = 1 and f f (x)/ x2 (x + 1)3, dx is a rational function, find the value of f'(0).

