Question: Refer to the function g shown in
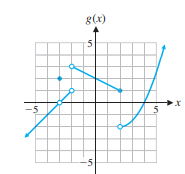
Refer to the function g shown in the figure. Use the graph to estimate the indicated function values and limits.
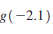
> Find the indicated quantities for f(x) = 3x2 .
>
> Use interval notation to specify the given interval.
> If the probability is .03 that an automobile tire fails in less than 50,000 miles, what is the probability that the tire does not fail in 50,000 miles?
> Use interval notation to specify the given interval.
> Use interval notation to specify the given interval.
> Use interval notation to specify the given interval. The set of all real numbers from -8 to -4, excluding -8 but including -4
> The graph shown represents the history of a person learning the material on limits and continuity in this book. At time t2, the student’s mind goes blank during a quiz. At time t4, the instructor explains a concept particularly well, th
> An office equipment rental and leasing company rents copiers for $10 per day (and any fraction thereof) or for $50 per 7-day week. Let C1x2 be the cost of renting a copier for x days.
> Table 2 shows the rates for natural gas charged by the Middle Tennessee Natural Gas Utility District during winter months. The base charge is a fixed monthly charge, independent of the amount of gas used per month. (A) Write a piecewise definition of t
> Discuss the differences between the function S(x) = 15 + 10 [x] and R(x) defined in Problem 90. (The symbol [x] is defined in problems 75 and 76.)
> A bike rental service charges $15 for the first hour (or any fraction thereof) and $10 for each additional hour (or fraction thereof) up to a maximum of 8 hours. (A) Write a piecewise definition of the charge R(x) for a rental lasting x hours. (B) Grap
> The function ((x) = 6 / (x – 4) satisfies ((2) = -3 and ((7) = 2. Is ( equal to 0 anywhere on the interval (0, 9)? Does this contradict Theorem 2? Explain.
> Sketch a possible graph of a function ( that is continuous for all real numbers and satisfies the given conditions. Find the x intercepts of (. ((x) > 0 on (1 - ∞, -3) and (2, 7); ( (x) < 0 on (-3, 2) and ( 7 , ∞)
> A keypad at the entrance of a building has 10 buttons labeled 0 through 9. What is the probability of a person correctly guessing a 4-digit entry code if they know that no digits repeat
> Sketch a possible graph of a function ( that is continuous for all real numbers and satisfies the given conditions. Find the x intercepts of (. ((x) > 0 on (- ∞, -4) and (3, ∞); ( (x) 6 0 on (-4, 3)
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. The greatest integer function is a rational function.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If ( is a function that is continuous on the open interval (0, 2), then f is continuous at x = 1.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. A rational function is continuous for all but finitely many real numbers.
> Refer to the greatest integer function, which is denoted by (x) and is defined as A) Is f continuous from the right at x = 2? (B) Is f continuous from the left at x = 2? (C) Is f continuous on the open interval (1, 2)? (D) Is f continuous on the clo
> Graph f, locate all points of discontinuity, and discuss the behavior of f at these points.
> Graph f, locate all points of discontinuity, and discuss the behavior of f at these points.
> Graph f, locate all points of discontinuity, and discuss the behavior of f at these points.
> Use Theorem 1 to determine where each function Express the answer in interval notation.
> Use Theorem 1 to determine where each function Express the answer in interval notation.
> In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Compute the probability that the number drawn is: Prime or less than 14.
> Use Theorem 1 to determine where each function Express the answer in interval notation.
> Use Theorem 1 to determine where each function Express the answer in interval notation.
> Use a graphing calculator to approximate the partition numbers of each function f(x) to four decimal places. Then solve the following inequalities: (A) f (x) (B) f (x) Express answers in interval notation.
> Use a graphing calculator to approximate the partition numbers of each function f(x) to four decimal places. Then solve the following inequalities: (A) f (x) (B) f (x) Express answers in interval notation.
> Use the graph of g to determine where (A) g(x) 7 0 (B) g(x) 6 0 Express answers in interval notation.
> Use a sign chart to solve each inequality. Express answers in inequality and interval notation.
> Use a sign chart to solve each inequality. Express answers in inequality and interval notation.
> Use a sign chart to solve each inequality. Express answers in inequality and interval notation.
> Use a sign chart to solve each inequality. Express answers in inequality and interval notation.
> Find all partition numbers of the function.
> In a family with 3 children, excluding multiple births, what is the probability of having 2 boys and 1 girl, in any order? Assume that a boy is as likely as a girl at each birth.
> Find all partition numbers of the function.
> Find all partition numbers of the function.
> Use Theorem 1 to determine where each function.
> use the four-step process to find f = (x) and then find  = 112, = 122, and  = 132.
> Use Theorem 1 to determine where each function.
> Use Theorem 1 to determine where each function.
> Use Theorem 1 to determine where each function.
> Refer to the function g shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function g shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function g shown in the figure. Use the graph to estimate the indicated function values and limits.
> In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Compute the probability that the number drawn is: A multiple of 3 or a multiple of 4.
> Without using a calculator, determine which event, E or F, is more likely to occur.
> Refer to the function f shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function f shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function f shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function f shown in the figure. Use the graph to estimate the indicated function values and limits.
> Sketch a possible graph of a function that satisfies the given conditions at x = 1 and discuss the continuity of f at x = 1.
> Sketch a possible graph of a function that satisfies the given conditions at x = 1 and discuss the continuity of f at x = 1.
> Sketch a possible graph of a function that satisfies the given conditions at x = 1 and discuss the continuity of f at x = 1.
> Refer to the following graph of y = f (x).
> Find an equation of the form Ax + By = C for the given line. The line through (-1, 20) and (1, 30)
> Using the probability assignments in Problem 27C, what is the probability that a random customer will not choose brand J or brand P? Data from problem 27C, :
> Find an equation of the form Ax + By = C for the given line. The line through (8, -4) that has slope -3
> Find an equation of the form Ax + By = C for the given line. The horizontal line through (7, 1)
> Find an equation of the form Ax + By = C for the given line. The vertical line through (5, 0)
> Repeat Problem 91 for the CTE of copper (column 3 of Table 10). Data from Problem 91: The coefficient of thermal expansion (CTE) is a measure of the expansion of an object subjected to extreme temperatures. To model this coefficient, we use a Michaelis&
> Institute of Chemistry, Macedonia) lists data for the substrate sucrose treated with the enzyme invertase. We want to model these data with a Michaelis–Menten function.
> A company producing computer components has established that, on average, a new employee can assemble N(t) components per day after t days of on-the-job training, as given by. (A) How many components per day can a new employee assemble after 6 days of o
> A drug is administered to a patient through an injection. The drug concentration (in milligrams/ milliliter) in the bloodstream t hours after the injection is
> A newly released smartphone operating system gives users an immediate notice to update but no further reminders. The percent P of users that have installed the new update after t days is given by (A) What percentage of users have installed the new update
> A company manufacturing surfboards has fixed costs of $300 per day and total costs of $5,100 per day for a daily output of 20 boards.
> Theorem 3 also states that. What conditions must n and an satisfy for the limit to be ∞? For the limit to be - ∞?
> In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Compute the probability that the number drawn is: Less than 10 or greater than 10.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. The graph of a rational function cannot cross a horizontal asymptote.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. A rational function has at most one horizontal asymptote.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. A rational function has at most one vertical asymptote.
> Give a limit expression that describes the left end behavior of the function.
> Give a limit expression that describes the left end behavior of the function.
> Give a limit expression that describes the right end behavior of the function.
> Give a limit expression that describes the right end behavior of the function.
> Find all horizontal and vertical asymptotes.
> Find all horizontal and vertical asymptotes.
> Find all horizontal and vertical asymptotes.
> Using the probability assignments in Problem 27C, what is the probability that a random customer will not choose brand S? Data from problem 27C,:
> Find all horizontal and vertical asymptotes.
> Find all horizontal and vertical asymptotes.
> Find all horizontal and vertical asymptotes.
> Find all horizontal and vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Compute the probability that the number drawn is: Even or a multiple of 7.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find each limit. Use - ∞ and ∞ when appropriate.

