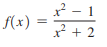Question: Find all horizontal and vertical asymptotes. /
> Find all partition numbers of the function.
> In a family with 3 children, excluding multiple births, what is the probability of having 2 boys and 1 girl, in any order? Assume that a boy is as likely as a girl at each birth.
> Find all partition numbers of the function.
> Find all partition numbers of the function.
> Use Theorem 1 to determine where each function.
> use the four-step process to find f = (x) and then find  = 112, = 122, and  = 132.
> Use Theorem 1 to determine where each function.
> Use Theorem 1 to determine where each function.
> Use Theorem 1 to determine where each function.
> Refer to the function g shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function g shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function g shown in the figure. Use the graph to estimate the indicated function values and limits.
> In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Compute the probability that the number drawn is: A multiple of 3 or a multiple of 4.
> Without using a calculator, determine which event, E or F, is more likely to occur.
> Refer to the function g shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function f shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function f shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function f shown in the figure. Use the graph to estimate the indicated function values and limits.
> Refer to the function f shown in the figure. Use the graph to estimate the indicated function values and limits.
> Sketch a possible graph of a function that satisfies the given conditions at x = 1 and discuss the continuity of f at x = 1.
> Sketch a possible graph of a function that satisfies the given conditions at x = 1 and discuss the continuity of f at x = 1.
> Sketch a possible graph of a function that satisfies the given conditions at x = 1 and discuss the continuity of f at x = 1.
> Refer to the following graph of y = f (x).
> Find an equation of the form Ax + By = C for the given line. The line through (-1, 20) and (1, 30)
> Using the probability assignments in Problem 27C, what is the probability that a random customer will not choose brand J or brand P? Data from problem 27C, :
> Find an equation of the form Ax + By = C for the given line. The line through (8, -4) that has slope -3
> Find an equation of the form Ax + By = C for the given line. The horizontal line through (7, 1)
> Find an equation of the form Ax + By = C for the given line. The vertical line through (5, 0)
> Repeat Problem 91 for the CTE of copper (column 3 of Table 10). Data from Problem 91: The coefficient of thermal expansion (CTE) is a measure of the expansion of an object subjected to extreme temperatures. To model this coefficient, we use a Michaelis&
> Institute of Chemistry, Macedonia) lists data for the substrate sucrose treated with the enzyme invertase. We want to model these data with a Michaelis–Menten function.
> A company producing computer components has established that, on average, a new employee can assemble N(t) components per day after t days of on-the-job training, as given by. (A) How many components per day can a new employee assemble after 6 days of o
> A drug is administered to a patient through an injection. The drug concentration (in milligrams/ milliliter) in the bloodstream t hours after the injection is
> A newly released smartphone operating system gives users an immediate notice to update but no further reminders. The percent P of users that have installed the new update after t days is given by (A) What percentage of users have installed the new update
> A company manufacturing surfboards has fixed costs of $300 per day and total costs of $5,100 per day for a daily output of 20 boards.
> Theorem 3 also states that. What conditions must n and an satisfy for the limit to be ∞? For the limit to be - ∞?
> In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Compute the probability that the number drawn is: Less than 10 or greater than 10.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. The graph of a rational function cannot cross a horizontal asymptote.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. A rational function has at most one horizontal asymptote.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. A rational function has at most one vertical asymptote.
> Give a limit expression that describes the left end behavior of the function.
> Give a limit expression that describes the left end behavior of the function.
> Give a limit expression that describes the right end behavior of the function.
> Give a limit expression that describes the right end behavior of the function.
> Find all horizontal and vertical asymptotes.
> Find all horizontal and vertical asymptotes.
> Find all horizontal and vertical asymptotes.
> Using the probability assignments in Problem 27C, what is the probability that a random customer will not choose brand S? Data from problem 27C,:
> Find all horizontal and vertical asymptotes.
> Find all horizontal and vertical asymptotes.
> Find all horizontal and vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Use - ∞ or ∞ where appropriate to describe the behavior at each zero of the denominator and identify all vertical asymptotes.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Compute the probability that the number drawn is: Even or a multiple of 7.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find each limit. Use - ∞ and ∞ when appropriate.
> Find each limit. Use - ∞ and ∞ when appropriate.
> Find each limit. Use - ∞ and ∞ when appropriate.
> In a family with 2 children, excluding multiple births, what is the probability of having 2 girls? Assume that a girl is as likely as a boy at each birth.
> Find each limit. Use - ∞ and ∞ when appropriate.
> Refer to the following graph of y = f (x).
> Refer to the following graph of y = f (x).
> Refer to the following graph of y = f (x).
> Factor each polynomial into the product of first-degree factors with integer coefficients.
> Factor each polynomial into the product of first-degree factors with integer coefficients.
> Factor each polynomial into the product of first-degree factors with integer coefficients.
> Factor each polynomial into the product of first-degree factors with integer coefficients.
> Refer to Problem 97. The average fee per ton of pollution is given by A(x) = F(x) >x. Write a piecewise definition of A(x). What is the limit of A(x) as x approaches 4,000 tons? As x approaches 8,000 tons? Data from Problem 97: A state charges polluters
> Assume that the volume discounts in Table 1 apply only to that portion of the volume in each interval. That is, the discounted price for a $4,000 purchase would be computed as follows: 300 + 0.9717002 + 0.9512,0002 + 0.9311,0002 = 3,809 (A) If x is the
> A single card is drawn from a standard 52-card deck. Let D be the event that the card drawn is a diamond, and let F be the event that the card drawn is a face card. find the indicated probabilities. Answer:
> Refer to Problems 91 and 92. Write a brief verbal comparison of the two services described for customers who use a car for more than 10 hours in a month. A company sells custom embroidered apparel and promotional products. Table 1 shows the volume disco
> A car sharing service offers a membership plan with no monthly fee. Members who use a car for at most 10 hours are charged $15 per hour. Members who use a car for more than 10 hours are charged $10 per hour.
> Let Æ’ be defined by.
> Compute the following limit for each function in Problems.
> Compute the following limit for each function.
> Compute the following limit for each function.
> Compute the following limit for each function.
> Is the limit expression a 0>0 indeterminate form? Find the limit or explain why the limit does not exist.
> Is the limit expression a 0>0 indeterminate form? Find the limit or explain why the limit does not exist.
> Is the limit expression a 0>0 indeterminate form? Find the limit or explain why the limit does not exist.
> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of drawing 1 card from a standard 52-card deck , what is the probability of drawing. Figure 4: A six or club.
> Is the limit expression a 0>0 indeterminate form? Find the limit or explain why the limit does not exist.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.