Question: Relate to the function whose graph is
Relate to the function whose graph is sketched in Fig. 12.
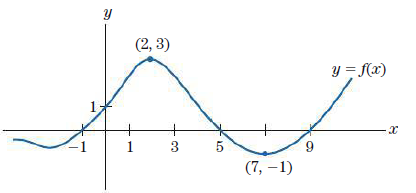
What is the range of f?
Transcribed Image Text:
(2, 3) y = f(x) + 1 + 5 (7, –1)
> Exercises 43–46 relate to Fig. 13. When a drug is injected into a person’s muscle tissue, the concentration y of the drug in the blood is a function of the time elapsed since the injection. The graph of a typical time&
> Simplify (100)3/2 and (.001)1/3.
> Simplify (81)3/4, 85/3, and (.25)-1.
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. h(f (x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. f (h(x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. h(g(x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. g(h(x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. g(f (x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. f (g(x))
> Let f (x) = x6, g(x) = x / 1 - x, and h(x) = x3 - 5x2 + 1. Calculate the following functions. h (f (t))
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) + g(x)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. g(x) - h(x - 3)
> Relate to the function whose graph is sketched in Fig. 12. For what values of x is f (x) ≤ 0? (2, 3) y = f(x) + 1 + 5 (7, –1)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) + h(x)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. g(x) - h(x)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) - g(x + 1)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) - g(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. g(x)h(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x)/h(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x)g(x)
> If f (x) = x2 - 3x, find f (0), f (5), f (3), and f (-7).
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x)h(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x) - g(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x) + g(x)
> Relate to the function whose graph is sketched in Fig. 12. For what values of x is f (x) ≤ 0? (2, 3) y = f(x) + 1 + 5 (7, –1)
> Find the points of intersection of the curves y = -x2 + x + 1 and y = x - 5.
> Find the points of intersection of the curves y = 5x2 - 3x – 2 and y = 2x - 1.
> Find the zeros of the quadratic function y = -2x2 - x + 2.
> Find the zeros of the quadratic function y = 5x2 - 3x - 2.
> Factor the polynomials. x5 - x4 - 2x3
> Factor the polynomials. 18 + 3x - x2
> Let f (x) = x6, g(x) = x / 1 - x, and h(x) = x3 - 5x2 + 1. Calculate the following functions. f (g(x))
> Factor the polynomials. 3x2 - 3x - 60
> Factor the polynomials. 5x3 + 15x2 - 20x
> Is the point (1, -2) on the graph of the function k(x) = x2 + (2/x)?
> Is the point (1/2, - 3/5) on the graph of the function h(x) = (x2 - 1)/(x2 + 1)?
> Relate to the function whose graph is sketched in Fig. 12. For what values of x does f (x) = 0? (2, 3) y = f(x) + 1 + 5 (7, –1)
> Draw the following intervals on the number line. [1, 3/2]
> Determine the domains of the following functions. f (x) = 1 /√(3x)
> Determine the domains of the following functions. f (x) = √(x2 + 1)
> Determine the domains of the following functions. f (x) = √(x – 1)
> What is the difference between an open interval and a closed interval from a to b?
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. h(1/x2)
> What are the four types of inequalities, and what do they each mean?
> Explain the relationships and differences among real numbers, rational numbers, and irrational numbers.
> Explain how to find f (a) geometrically from the graph of y = f (x).
> Explain how to solve f (x) = b geometrically from the graph of y = f (x).
> In the formula A = P(1 + i)n, what do A, P, i, and n represent?
> State the six laws of exponents.
> Give two methods for finding the zeros of a quadratic function.
> What is a zero of a function?
> What five operations on functions are discussed in this chapter? Give an example of each.
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. g(1 / u)
> What is meant by the absolute value of a number?
> Define and give an example of each of the following types of functions. (a) quadratic function (b) polynomial function (c) rational function (d) power function
> What is a quadratic function? What shape does its graph have?
> What are the x- and y-intercepts of a function, and how are they found?
> What is a linear function? Constant function? Give examples.
> What is the graph of a function, and how is it related to vertical lines?
> What is meant by the domain and range of a function?
> Relate to the function whose graph is sketched in Fig. 12. Is f (6) positive or negative? (2, 3) y = f(x) + 1 + 5 (7, –1)
> What is meant by “the value of a function at x”?
> What is a function?
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. f(1 / t)
> Assign variables to the dimensions of the geometric object. Rectangular box with height =- length
> Assign variables to the dimensions of the geometric object. Rectangular box with square base
> Assign variables to the dimensions of the geometric object. Norman window: Rectangle topped with a semicircle
> Assign variables to the dimensions of the geometric object. Rectangle with height = 3 . width
> A store estimates that the total revenue (in dollars) from the sale of x bicycles per year is given by the function R(x) = 250x - .2x2. (a) Graph R(x) in the window [200, 500] by [42000, 75000]. (b) What sales level produces a revenue of $63,000? (c) Wha
> The daily cost (in dollars) of producing x units of a certain product is given by the function C(x) = 225 + 36.5x - .9x2 + .01x3. (a) Graph C(x) in the window [0, 70] by [ -400, 2000]. (b) What is the cost of producing 50 units of goods? (c) Consider the
> A ball thrown straight up into the air has height -16x2 + 80x feet after x seconds. (a) Graph the function in the window [0, 6] by [ -30, 120]. (b) What is the height of the ball after 3 seconds? (c) At what times will the height be 64 feet? (d) At what
> A ball is thrown straight up into the air. The function h(t) gives the height of the ball (in feet) after t seconds. In Exercises 45–50, translate the task into both a statement involving the function and a statement involving the graph of the function.
> Relate to the function whose graph is sketched in Fig. 12. Is f (4) positive or negative? (2, 3) y = f(x) + 1 + 5 (7, –1)
> A ball is thrown straight up into the air. The function h(t) gives the height of the ball (in feet) after t seconds. In Exercises 45–50, translate the task into both a statement involving the function and a statement involving the graph of the function.
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. g(x + 5) / f (x + 5)
> Evaluate each of the functions in Exercises 37–42 at the given value of x. f (x) = |x|, x = -2.5
> A ball is thrown straight up into the air. The function h(t) gives the height of the ball (in feet) after t seconds. In Exercises 45–50, translate the task into both a statement involving the function and a statement involving the graph of the function.
> A ball is thrown straight up into the air. The function h(t) gives the height of the ball (in feet) after t seconds. In Exercises 45–50, translate the task into both a statement involving the function and a statement involving the graph of the function.
> A ball is thrown straight up into the air. The function h(t) gives the height of the ball (in feet) after t seconds. In Exercises 45–50, translate the task into both a statement involving the function and a statement involving the graph of the function.
> A ball is thrown straight up into the air. The function h(t) gives the height of the ball (in feet) after t seconds. In Exercises 45–50, translate the task into both a statement involving the function and a statement involving the graph of the function.
> Refer to the profit function in Fig. 19. Translate the task “find P(2000)” into a task involving the graph. 52,500 y= P(x) 2500 Figure 19 A profit function.
> Refer to the profit function in Fig. 19. Translate the task “solve P(x) = 30,000” into a task involving the graph of the function. 52,500 y= P(x) 2500 Figure 19 A profit function.
> Refer to the profit function in Fig. 19. The point (1500, 42,500) is on the graph of the function. Restate this fact in terms of the function P(x). 52,500 y= P(x) 2500 Figure 19 A profit function.
> Refer to the profit function in Fig. 19. The point (2500, 52,500) is the highest point on the graph of the function. What does this say in terms of profit versus quantity? 52,500 y= P(x) 2500 Figure 19 A profit function.
> Refer to the cost function in Fig. 18. If 500 units of goods are produced, estimate the cost of producing 100 more units of goods? y = C(x) 3397 2875 Б00 700 Figure 18 A cost function.
> Relate to the function whose graph is sketched in Fig. 12. Find f (2) and f (-1). (2, 3) y = f(x) + 1 + 5 (7, –1)
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. f (x + 2) + g(x + 2)
> Refer to the cost function in Fig. 18. Translate the task “find C(400)” into a task involving the graph. y = C(x) 3397 2875 Б00 700 Figure 18 A cost function.
> Refer to the cost function in Fig. 18. Translate the task “solve C(x) = 3500 for x” into a task involving the graph of the function. y = C(x) 3397 2875 Б00 700 Figure 18 A cost function.
> Refer to the cost function in Fig. 18. The point (1000, 4000) is on the graph of the function. Restate this fact in terms of the function C(x). y = C(x) 3397 2875 Б00 700 Figure 18 A cost function.
> Refer to the cost and revenue functions in Fig. 17. The cost of producing x units of goods is C(x) dollars and the revenue from selling x units of goods is R(x) dollars. What is the profit from the manufacture and sale of 30 units of goods? y = R(x
> Refer to the cost and revenue functions in Fig. 17. The cost of producing x units of goods is C(x) dollars and the revenue from selling x units of goods is R(x) dollars. At what level of production is the cost $1400? y = R(x) y = C(x) 1800 1400 100
> Refer to the cost and revenue functions in Fig. 17. The cost of producing x units of goods is C(x) dollars and the revenue from selling x units of goods is R(x) dollars. At what level of production is the revenue $1400? y = R(x) y = C(x) 1800 1400
> Refer to the cost and revenue functions in Fig. 17. The cost of producing x units of goods is C(x) dollars and the revenue from selling x units of goods is R(x) dollars. What are the revenue and cost from the production and sale of 30 units of goods?
> Refer to the function f (r), which gives the cost (in cents) of constructing a 100-cubic-inch cylinder of radius r inches. The graph of f (r) is shown in Fig. 16. How much is saved by increasing the radius from 1 inch to 3 inches? 400 (1, 330) (6.87
> Refer to the function f (r), which gives the cost (in cents) of constructing a 100-cubic-inch cylinder of radius r inches. The graph of f (r) is shown in Fig. 16. What is the additional cost of increasing the radius from 3 inches to 6 inches? 400 (1
> Refer to the function f (r), which gives the cost (in cents) of constructing a 100-cubic-inch cylinder of radius r inches. The graph of f (r) is shown in Fig. 16. Interpret the fact that the point (3, 162) is the lowest point on the graph of the functio
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. f (x + 1) g(x + 1)
> Relate to the function whose graph is sketched in Fig. 12. Find f (0) and f (7). (2, 3) y = f(x) + 1 + 5 (7, –1)
> Refer to the function f (r), which gives the cost (in cents) of constructing a 100-cubic-inch cylinder of radius r inches. The graph of f (r) is shown in Fig. 16. Interpret the fact that the point (3, 162) is on the graph of the function. 400 (1, 33

