Question: Relate to the function whose graph is
Relate to the function whose graph is sketched in Fig. 12.
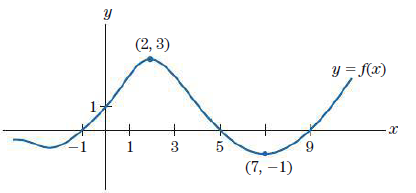
For what values of x is f (x) ≤ 0?
Transcribed Image Text:
(2, 3) y = f(x) + 1 + 5 (7, –1)
> Exercises 43–46 relate to Fig. 13. When a drug is injected into a person’s muscle tissue, the concentration y of the drug in the blood is a function of the time elapsed since the injection. The graph of a typical time&
> Let f (x) = x6, g(x) = x / 1 - x, and h(x) = x3 - 5x2 + 1. Calculate the following functions. g (h(t))
> Find an equation of the given line. Slope is 2; (1, -2) on line
> Find an equation of the given line. Slope is -1; (7, 1) on line
> Find the slopes and y-intercepts of the following lines. 4x + 9y = -1
> Find the slopes and y-intercepts of the following lines. y = x/7 - 5
> Find the slopes and y-intercepts of the following lines. y = 6
> Determine the domains of the following functions. f (x) = 1 / x(x + 3)
> Let f (x) = [1/(x + 1)] - x2. Evaluate f (a + 1).
> Let f (x) = x2 - 2. Evaluate f (a - 2).
> Let f (x) = 2x + 3x2. Evaluate f (0), f (- 1/4), and f (1/√2).
> Let f (x) = x3 +1 /x. Evaluate f (1), f (3), f (-1), f (- 12), and f (√2).
> Let f (x) = x6, g(x) = x / 1 - x, and h(x) = x3 - 5x2 + 1. Calculate the following functions. g (f (x))
> Exercises 43–46 relate to Fig. 13. When a drug is injected into a person’s muscle tissue, the concentration y of the drug in the blood is a function of the time elapsed since the injection. The graph of a typical time&
> Suppose that $7000 is deposited in a savings account that pays a rate of interest r per annum, compounded annually, for 20 years. (a) Express the account balance A(r) as a function of r. (b) Calculate the account balance for r = .07 and r = .12.
> Suppose that $15,000 is deposited in a savings account that pays a rate of interest r per annum, compounded annually, for 10 years. (a) Express the account balance A(r) as a function of r. (b) Calculate the account balance for r = 0.04 and r = 0.06
> Suppose that $7000 is deposited in a savings account that pays 9% per annum, compounded biannually, for t years. (a) Express the account balance A(t) as a function of t, the number of years that the principal has been in the account. (b) Calculate the ac
> Suppose that $15,000 is deposited in a savings account that pays 4% per annum, compounded monthly, for t years. (a) Express the account balance A(t) as a function of t, the number of years that the principal has been in the account. (b) Calculate the acc
> Use the laws of exponents to simplify the algebraic expressions. 3√x (8x2/3)
> Use the laws of exponents to simplify the algebraic expressions. x3/2/ √x
> Use the laws of exponents to simplify the algebraic expressions. xy3 / x-5y6
> Use the laws of exponents to simplify the algebraic expressions. (√(x + 1))4
> The revenue R(x) (in thousands of dollars) that a company receives from the sale of x thousand units is given by R(x) = 5x - x2. The sales level x is in turn a function f (d) of the number d of dollars spent on advertising, where Express the revenue as
> Let f (x) = x6, g(x) = x / 1 - x, and h(x) = x3 - 5x2 + 1. Calculate the following functions. h(g(x))
> The population of a city is estimated to be 750 + 25t + .1t2 thousand people t years from the present. Ecologists estimate that the average level of carbon monoxide in the air above the city will be 1 + .4x ppm (parts per million) when the population is
> Exercises 43–46 relate to Fig. 13. When a drug is injected into a person’s muscle tissue, the concentration y of the drug in the blood is a function of the time elapsed since the injection. The graph of a typical time&
> Simplify (100)3/2 and (.001)1/3.
> Simplify (81)3/4, 85/3, and (.25)-1.
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. h(f (x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. f (h(x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. h(g(x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. g(h(x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. g(f (x))
> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. f (g(x))
> Let f (x) = x6, g(x) = x / 1 - x, and h(x) = x3 - 5x2 + 1. Calculate the following functions. h (f (t))
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) + g(x)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. g(x) - h(x - 3)
> Relate to the function whose graph is sketched in Fig. 12. For what values of x is f (x) ≤ 0? (2, 3) y = f(x) + 1 + 5 (7, –1)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) + h(x)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. g(x) - h(x)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) - g(x + 1)
> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) - g(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. g(x)h(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x)/h(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x)g(x)
> If f (x) = x2 - 3x, find f (0), f (5), f (3), and f (-7).
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x)h(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x) - g(x)
> Let f (x) = x2 - 2x, g(x) = 3x - 1, and h(x) = √x. Find the following functions. f (x) + g(x)
> Find the points of intersection of the curves y = -x2 + x + 1 and y = x - 5.
> Find the points of intersection of the curves y = 5x2 - 3x – 2 and y = 2x - 1.
> Find the zeros of the quadratic function y = -2x2 - x + 2.
> Find the zeros of the quadratic function y = 5x2 - 3x - 2.
> Factor the polynomials. x5 - x4 - 2x3
> Factor the polynomials. 18 + 3x - x2
> Let f (x) = x6, g(x) = x / 1 - x, and h(x) = x3 - 5x2 + 1. Calculate the following functions. f (g(x))
> Factor the polynomials. 3x2 - 3x - 60
> Factor the polynomials. 5x3 + 15x2 - 20x
> Is the point (1, -2) on the graph of the function k(x) = x2 + (2/x)?
> Is the point (1/2, - 3/5) on the graph of the function h(x) = (x2 - 1)/(x2 + 1)?
> Relate to the function whose graph is sketched in Fig. 12. For what values of x does f (x) = 0? (2, 3) y = f(x) + 1 + 5 (7, –1)
> Draw the following intervals on the number line. [1, 3/2]
> Determine the domains of the following functions. f (x) = 1 /√(3x)
> Determine the domains of the following functions. f (x) = √(x2 + 1)
> Determine the domains of the following functions. f (x) = √(x – 1)
> What is the difference between an open interval and a closed interval from a to b?
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. h(1/x2)
> What are the four types of inequalities, and what do they each mean?
> Explain the relationships and differences among real numbers, rational numbers, and irrational numbers.
> Explain how to find f (a) geometrically from the graph of y = f (x).
> Explain how to solve f (x) = b geometrically from the graph of y = f (x).
> In the formula A = P(1 + i)n, what do A, P, i, and n represent?
> State the six laws of exponents.
> Relate to the function whose graph is sketched in Fig. 12. What is the range of f? (2, 3) y = f(x) + 1 + 5 (7, –1)
> Give two methods for finding the zeros of a quadratic function.
> What is a zero of a function?
> What five operations on functions are discussed in this chapter? Give an example of each.
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. g(1 / u)
> What is meant by the absolute value of a number?
> Define and give an example of each of the following types of functions. (a) quadratic function (b) polynomial function (c) rational function (d) power function
> What is a quadratic function? What shape does its graph have?
> What are the x- and y-intercepts of a function, and how are they found?
> What is a linear function? Constant function? Give examples.
> What is the graph of a function, and how is it related to vertical lines?
> What is meant by the domain and range of a function?
> Relate to the function whose graph is sketched in Fig. 12. Is f (6) positive or negative? (2, 3) y = f(x) + 1 + 5 (7, –1)
> What is meant by “the value of a function at x”?
> What is a function?
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. f(1 / t)
> Assign variables to the dimensions of the geometric object. Rectangular box with height =- length
> Assign variables to the dimensions of the geometric object. Rectangular box with square base
> Assign variables to the dimensions of the geometric object. Norman window: Rectangle topped with a semicircle
> Assign variables to the dimensions of the geometric object. Rectangle with height = 3 . width
> A store estimates that the total revenue (in dollars) from the sale of x bicycles per year is given by the function R(x) = 250x - .2x2. (a) Graph R(x) in the window [200, 500] by [42000, 75000]. (b) What sales level produces a revenue of $63,000? (c) Wha
> The daily cost (in dollars) of producing x units of a certain product is given by the function C(x) = 225 + 36.5x - .9x2 + .01x3. (a) Graph C(x) in the window [0, 70] by [ -400, 2000]. (b) What is the cost of producing 50 units of goods? (c) Consider the
> A ball thrown straight up into the air has height -16x2 + 80x feet after x seconds. (a) Graph the function in the window [0, 6] by [ -30, 120]. (b) What is the height of the ball after 3 seconds? (c) At what times will the height be 64 feet? (d) At what
> A ball is thrown straight up into the air. The function h(t) gives the height of the ball (in feet) after t seconds. In Exercises 45–50, translate the task into both a statement involving the function and a statement involving the graph of the function.
> Relate to the function whose graph is sketched in Fig. 12. Is f (4) positive or negative? (2, 3) y = f(x) + 1 + 5 (7, –1)
> A ball is thrown straight up into the air. The function h(t) gives the height of the ball (in feet) after t seconds. In Exercises 45–50, translate the task into both a statement involving the function and a statement involving the graph of the function.
> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. g(x + 5) / f (x + 5)

