Question: Show that the function is continuous on (-∞, ∞). /
Show that the function is continuous on (-∞, ∞).
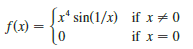
Transcribed Image Text:
[x* sin(1/x) if x # 0 f(x) = if x= 0
> Let F (x) = x2 – 1/|x – 1|. (a) Find (i). limx→1+ F (x) (ii). limx→1- F (x) (b). Does limx→1 F (x) exist? (c). Sketch the graph of F.
> Find the limit, if it exists. If the limit does not exist, explain why. 2x + 12 lim I-6 |x + 6||
> Prove that limx→0+ √x esinπ/x = 0.
> If 2x < g (x) < x4 – x2 + 2 for all x, evaluate limx→1 g (x).
> If 4x – 9 < f (x) < x2 – 4x + 7 for x > 0, find limx→4 f (x).
> Use the Squeeze Theorem to show that limx→0 √x3 + x2 sin π/x = 0 Illustrate by graphing the functions f, g and h (in the notation of the Squeeze Theorem) on the same screen.
> (a). Estimate the value of limx→0 x/ 1 + 3x – 1 by graphing the function f (x) = x/ (√1 + 3x – 1). (b). Make a table of values of f (x) for x close to 0 and guess the value of the limit. (c). Use the Limit Laws to prove that your guess is correct.
> Evaluate the limit, if it exists. lim x → -4 √x2 + 9 – 5/ x + 4
> Evaluate the limit, if it exists. lim t → 0 (1/t√1 + t – 1/t)
> The point P (1, 0) lies on the curve y = sin (10π/x). (a). If Q is the point (x, sin (10π/x)), find the slope of the secant line PQ (correct to four decimal places) for x = 2, 1.5, 1.4, 1.3, 1.2, 1.1, 0.5, 0.6, 0.7, 0.8, and 0.9. Do the slopes appear to
> Evaluate the limit, if it exists. lim t → 0 (1/t – 1/t2 + t)
> Evaluate the limit, if it exists. lim x → 16 4 - √x / 16x – x2
> Evaluate the limit, if it exists. lim x → -1 x2 + 2x + 1/ x4 - 1
> Explain what it means to say that limx→1- = f (x) = 3 and limx→1+ = f (x) = 7 In this situation is it possible that limx→1 = f (x) = 5 exists? Explain.
> Evaluate the limit, if it exists. lim h → 0 √1 + h - 1/h
> Evaluate the limit, if it exists. lim x → 2 x + 2 / x3 + 8
> Evaluate the limit, if it exists. lim h → 0 (2 + h)3 – 8 / h
> Evaluate the limit, if it exists. lim x → -1 x2 – 4x / x2 – 3x - 4
> Evaluate the limit, if it exists. lim x → -3 t2 - 9 + 1/ 2x2 + 7t + 3
> Evaluate the limit, if it exists. lim x → -1 2x2 + 3x + 1/ x2 - 2x – 3
> (a). What is wrong with the following equation? x2 + x – 6/ x - 2 = x + 3 (b). In view of part (a), explain why the equation lim x →2 x2 + x - 6 x - 2 = lim x→2 (x + 3) is correct.
> Given that limx→2 f (x) = 4 limx→2 g (x) = -2 limx→2 h (x) = 0 find the limits that exist. If the limit does not exist, explain why. (a) lim [f(x) + 5g(x)] (b) lim [g(x)]° (c) lim F(x) 3f(x) (d)
> Use the graph of the function f to state the value of each limit, if it exists. If it does not exist, explain why. (a) lim f(x) (b) lim f(x) (c) lim f(x) 1 f(x): 1 + %3D
> Sketch the graph of the function and use it to determine the values of for which limx→a f (x) exists. (1+х if x << -1 f(x) = {x if –1<x<1 2 — х if x> 1
> If a rock is thrown upward on the planet Mars with a velocity of 10 m/s, its height in meters seconds later is given by y = 10t – 1.8t2 (a). Find the average velocity over the given time intervals: (i). [1, 2] (ii). [1, 1.5] (iii). [1, 1.1] (iv). [1, 1
> For the function whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. 4- -2 2 4 す (a) lim g(t) (b) lim g(t) (c) lim g(t) (d) lim g(t) (e) lim g(t) (f) lim g(1) -2+ (g) g(2) (h) lim g(t)
> For the function f whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. 4. 2- 4 2. (a) lim f(x) (b) lim f(x) (c) lim f(x) (d) lim f(x) (e) f(3)
> The displacement (in centimeters) of a particle moving back and forth along a straight line is given by the equation of motion s = 2 sin πt + 3 cos πt, where is measured in seconds. (a). Find the average velocity during each time period: (i). [1, 2] (ii
> The table shows the position of a cyclist. (a). Find the average velocity for each time period: (i). [1, 3] (ii). [2, 3] (iii). [3, 5] (iv). [3, 4] (b) Use the graph of as a function of to estimate the instantaneous velocity when t = 3. t (second
> If a ball is thrown into the air with a velocity of 40 ft/s, its height in feet seconds later is given by y = 40t – 16t2. (a). Find the average velocity for the time period beginning when t = 2 and lasting (i). 0.5 second (ii). 0.1 second (iii). 0.05 se
> The point P (0, 5, 0) lies on the curve y = cos πx. (a). If Q is the point (x, cos πx), use your calculator to find the slope of the secant line (correct to six decimal places) for the following values of x: (i). 0 (ii). 0.4 (iii). 0.49 (iv). 0.499 (v
> Find an equation of the tangent line to the curve at the given point. y = √x, (1, 1)
> A cardiac monitor is used to measure the heart rate of a patient after surgery. It compiles the number of heartbeats after t minutes. When the data in the table are graphed, the slope of the tangent line represents the heart rate in beats per minute. T
> If and are positive numbers, prove that the equation a/x3 + 2x2 – 1 + b/x3 + x – 2 = 0 has at least one solution in the interval (-1, 1).
> The figure shows a fixed circle C1 with equation (x -1)2 + y2 = 1 and a shrinking circle C2 with radius r and center the origin. P is the point (0, r), Q is the upper point of intersection of the two circles, and R is the point of intersection of the lin
> Find a formula for a function that has vertical asymptotes x = 1 and x = 3 and horizontal asymptote y = 1.
> Find a formula for a function that satisfies the following conditions: lim f(x) = 0, lim f(x) = -0, f(2) = 0, %3D lim f(x) = 0, lim f(x) = -0 %3D I-3+
> Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval. ex = 3 – 2x, (0, 1)
> A Tibetan monk leaves the monastery at 7:00 AM and takes his usual path to the top of the mountain, arriving at 7:00 PM. The following morning, he starts at 7:00 AM at the top and takes the same path back, arriving at the monastery at 7:00 PM. Use the In
> Is there a number that is exactly 1 more than its cube?
> Is there a number a such that limx→2 3x2 +ax + a+ 3/x2 + x - 2 exists? If so, find the value of a and the value of the limit.
> (a) Prove that the equation has at least one real root. (b) Use your graphing device to find the root correct to three decimal places. √x - 5 = 1/x + 3
> For the function whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. -4 -2 2 4 6 (a) lim h(x) (b) lim h(x) (c) lim h(x) --3- I--3+ --3 (d) h(-3) (e) lim h(x) (f) lim h(x) (g) lim h(x) (h) h(0) (i
> (a) Prove that the equation has at least one real root. (b) Use your graphing device to find the root correct to three decimal places. 100e-x/100 = 0.01x2
> (a). Prove that the equation has at least one real root. (b). Use your calculator to find an interval of length 0.01 that contains a root. ln x = 3 – 2x
> Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval. x4 + x - 3 = 0 (1, 2)
> Let f (x) = [[cos x]], -Ï€ (a). Sketch the graph of (b). Evaluate each limit, if it exists. (c). For what values of a does limx→ a f (x) exist? (i) lim f(x) (ii) lịm f(x) I-(m/2)- (iii) lim f(x) 1-(m/2)+ (iv) lim f(x) 1/
> (a). A tank contains 5000 L of pure water. Brine that contains 30 g of salt per liter of water is pumped into the tank at a rate of 25 L/min. Show that the concentration of salt after t minutes (in grams per liter) is (b). What happens to the concentra
> (a). Show that the absolute value function F (x) = |x| is continuous everywhere. (b). Prove that if f is a continuous function on an interval, then so is |f|. (c). Is the converse of the statement in part (b) also true? In other words, if |f| is continuo
> The graph shows the influence of the temperature T on the maximum sustainable swimming speed of Coho salmon. (a). What is the meaning of the derivative S'(T)? What are its units? (b). Estimate the values of S'(15) and S'(25) and interpret them. SA
> Let P and Q be polynomials. Find limx→∞ P (x)/Q (x) if the degree of P is (a) less than the degree of Q and (b) greater than the degree of Q.
> The quantity (in pounds) of a gourmet ground coffee that is sold by a coffee company at a price of p dollars per pound is Q = f (p). (a). What is the meaning of the derivative f' (8)? What are its units? (b). Is f'(8) positive or negative? Explain.
> Use the given graph of f to state the value of each quantity, if it exists. If it does not exist, explain why. 2- 4 2. 4, (a) lim f(x) (b) lim f(x) (c) lim f(x) (d) lim f(x) (e) f(5)
> A function is a ratio of quadratic functions and has a vertical asymptote x = 4 and just one x-intercept, x = 1. It is known that f has a removable discontinuity at x = -1 and limx→1 f (x) = 2. Evaluate (a). f (0) (b). limx→∞ f (x)
> The number of bacteria after t hours in a controlled laboratory experiment is n = f (t). (a). What is the meaning of the derivative f' (5)? What are its units? (b). Suppose there is an unlimited amount of space and nutrients for the bacteria. Which do yo
> The cost of producing x ounces of gold from a new gold mine C = f (x) is dollars. (a). What is the meaning of the derivative f'(x)? What are its units? (b). What does the statement f' (800) = 17 mean? (c). Do you think the values of f' (x) will increase
> (a). Graph the function f (x) = ex + ln |x – 4| for 0 < x < 5. Do you think the graph is an accurate representation of ? (b). How would you get a graph that represents f better?
> (a). Prove that the equation has at least one real root. (b). Use your calculator to find an interval of length 0.01 that contains a root. cos x = x3
> Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval. sin x = x2 - x (1, 2)
> The number N of US cellular phone subscribers (in millions) is shown in the table. (Midyear estimates are given.) (a). Find the average rate of cell phone growth (i). from 2002 to 2006 (ii). from 2002 to 2004 (iii). from 2000 to 2002 In each case, incl
> Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval. 3√x = 1 – x, (1, 0)
> Find the horizontal and vertical asymptotes of each curve. If you have a graphing device, check your work by graphing the curve and estimating the asymptotes. x — х У- - 6х + 5 x? — 6х + 5
> Suppose f is continuous on [1, 5] and the only solutions of the equation f (x) = 6 are x = 1 and x = 4. If f (2) = 8, explain why f (3) > 6.
> (a). Find the slope of the tangent line to the curve y = x – x3 at the point (1, 0) (i). using Definition 1 (ii). using Equation 2 (b). Find an equation of the tangent line in part (a). (c). Graph the curve and the tangent line in successively smaller v
> If f (x) = x2 + 10 sin x, show that there is a number c such that f (c) = 1000.
> Each limit represents the derivative of some function f at some number a. State such an f and a in each case. 1* + t - 2 lim t - 1
> Which of the following functions f has a removable discontinuity at a? If the discontinuity is removable, find a function g that agrees with f for x ≠a and is continuous at a. x* – 1 (a) f(x) = a = 1 X - 1 x' - x? – 2x (b) f(x) =
> Find the values of and that make continuous everywhere. x? – 4 - 4 if x<2 x - 2 f(x) = ax? – bx + 3 if 2 <x<3 2х — а + b if x> 3
> For what value of the constant is the function continuous f on (-∞, ∞)? Scx? - сх? + 2х if х<2 f(x): x³ - cx if x> 2 — сх
> Use a graph to determine how close to 2 we have to take to ensure that x3 – 3x + 4 is within a distance 0.2 of the number 6. What if we insist that x3 - 3x + 4 be within 0.1 of 6?
> Find the numbers at which the function is discontinuous. At which of these points is continuous from the right, from the left, or neither? Sketch the graph of f. x + 2 f(x) = {e* х+2 if x<0 if 0 <xs1 2 — х if x>1
> (a). Use numerical and graphical evidence to guess the value of the limit limx→1 x3 – 1/√x - 1 (b). How close to 1 does have to be to ensure that the function in part (a) is within a distance 0.5 of its limit?
> Show that f is continuous on (-∞, ∞). x? if x<1 Vx if x> 1 f(x) =
> (a). Evaluate h (x) = (tan x-x)/x3 for x = 1, 0.5, 0.1, 0.05, 0.01, and 0.005. (b). Guess the value of limx→0 tan x – x/x3. (c). Evaluate h (x) for successively smaller values of until you finally reach a value 0 of for h (x). Are you still confident tha
> (a). Find the slope of the tangent line to the parabola y = 4x – x2 at the point (1, 3) (i). using Definition 1 (ii). using Equation 2 (b). Find an equation of the tangent line in part (a). (c). Graph the parabola and the tangent line. As a check on you
> Find f' (a). f (t) = 2t + 1/t + 3
> Locate the discontinuities of the function and illustrate by graphing. y = ln (tan2x)
> Use continuity to evaluate the limit. limx→4 5 + √x/√5 + x
> (a). If G (x) = 4x2 – x2, find G' (x) and use it to find equations of the tangent lines to the curve y = 4x2 – x3 at the points (2, 8) and (3, 9). (b). Illustrate part (a) by graphing the curve and the tangent lines on the same screen.
> The point P (1, ½) lies on the curve y = x (1 + x). (a). If Q is the point (x, x/ (1 + x), use your calculator to find the slope of the secant line PQ correct to six decimal places) for the following values of x: (i). 0.5 (ii). 0.9 (iii). 0.99 (iv). 0
> (a). Evaluate the function f (x) = x2 – (2x/100) for x = 1 1, 0.8, 0.6, 0.4, 0.2, 0.1, and 0.05, and guess the value of limx→0 (x2 – 2x/1000) (b). Evaluate f (x) for x = 0.04, 0.02, 0.01, 0.005, 0.003, and 0.001. Guess again.
> The slope of the tangent line to the graph of the exponential function y = 2x at the point (0, 1) is limx→0 (2x – 1)/x. Estimate the slope to three decimal places.
> (a). Estimate the value of the limit limx→0 (1 + x)1/x to five decimal places. Does this number look familiar? (b). Illustrate part (a) by graphing the function y = (1 + x)1/x.
> (a). Estimate the value of limx→0 = sinx/sinπx by graphing the function f (x) = (sin x)/(sinπx). State your answer correct to two decimal places. (b). Check your answer in part (a) by evaluating f (x) for values of that approach 0.
> (a). By graphing the function f (x) = (cos2x – cos x)/x2 and zooming in toward the point where the graph crosses the y-axis, estimate the value of limx→0 f (x). (b). Check your answer in part (a) by evaluating f (x) for values of that approach 0.
> Use a table of values to estimate the value of the limit. If you have a graphing device, use it to confirm your result graphically. 9* - 5 lim -
> Use a table of values to estimate the value of the limit. If you have a graphing device, use it to confirm your result graphically. x6 - lim 10 1-1 x" - 1 1
> Use a table of values to estimate the value of the limit. If you have a graphing device, use it to confirm your result graphically. tan 3x lim 1-0 tan 5x
> (a). If F (x) = 5x / (1 + x2), find F' (2) and use it to find an equation of the tangent line to the curve y = 5x/ (1 + x2) at the point (2, 2). (b). Illustrate part (a) by graphing the curve and the tangent line on the same screen.
> Use a table of values to estimate the value of the limit. If you have a graphing device, use it to confirm your result graphically. Vx + 4 – 2 lim
> (a). Show that limx→∞ 4x2 – 5x/2x2 + 1 = 2. (b). By graphing the function in part (a) and the line y = 1.9 on a common screen, find a number N such that 4x2 – 5x/2x2 + 1 > 1.9 when x > N What if 1.9 is replaced by 1.99?
> (a). Show that lim x→∞ e-x/10 = 0. (b). By graphing y = e-x/10 and y = 0.1 on a common screen, discover how large you need to make x so that e-x/10 < 0.1. (c). Can you solve part (b) without using a graphing device?
> In Chapter 7 we will be able to show, under certain assumptions, that the velocity v (t) of a falling raindrop at time t is where t is the acceleration due to gravity and is the terminal velocity of the raindrop. (a). Find limt→â
> Guess the value of the limit (if it exists) by evaluating the function at the given numbers (correct to six decimal places). x? — 2х х 3 2.5, 2.1, 2.05, 2.01, 2.005, 2.001, lim x? — х — 2° 1.9, 1.95, 1.99, 1.995, 1.999
> Determine whether f'(0) exists.
> Determine whether f'(0) exists.
> Make a rough sketch of the curve y = xn (n an integer) for the following five cases: Then use these sketches to find the following limits.
> The quantity of oxygen that can dissolve in water depends on the temperature of the water. (So thermal pollution influences the oxygen content of water.) The graph shows how oxygen solubility varies as a function of the water temperature T. (a). What is
> By the end behavior of a function we mean the behavior of its values as x →∞ and as x →-∞. (a). Describe and compare the end behavior of the functions P (x) = 3x5 – 5x3 + 2x Q (x) 3x5 by graphing both functions in the viewing rectangles [-2, 2] by [-2, 2
> If and are continuous functions with f (3) = 5 and limx→3 [2 f (x) – g (x)] = 4, find g (3).

