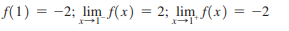Question: Sketch a possible graph of a function
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Compute the probability that the number drawn is: Even or a multiple of 7.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> Find each function value and limit. Use - ∞ or ∞ where appropriate.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find (A) the leading term of the polynomial, (B) the limit as x approaches ∞, and (C) the limit as x approaches - ∞.
> Find each limit. Use - ∞ and ∞ when appropriate.
> Find each limit. Use - ∞ and ∞ when appropriate.
> Find each limit. Use - ∞ and ∞ when appropriate.
> In a family with 2 children, excluding multiple births, what is the probability of having 2 girls? Assume that a girl is as likely as a boy at each birth.
> Find each limit. Use - ∞ and ∞ when appropriate.
> Refer to the following graph of y = f (x).
> Refer to the following graph of y = f (x).
> Refer to the following graph of y = f (x).
> Factor each polynomial into the product of first-degree factors with integer coefficients.
> Factor each polynomial into the product of first-degree factors with integer coefficients.
> Factor each polynomial into the product of first-degree factors with integer coefficients.
> Factor each polynomial into the product of first-degree factors with integer coefficients.
> Refer to Problem 97. The average fee per ton of pollution is given by A(x) = F(x) >x. Write a piecewise definition of A(x). What is the limit of A(x) as x approaches 4,000 tons? As x approaches 8,000 tons? Data from Problem 97: A state charges polluters
> Assume that the volume discounts in Table 1 apply only to that portion of the volume in each interval. That is, the discounted price for a $4,000 purchase would be computed as follows: 300 + 0.9717002 + 0.9512,0002 + 0.9311,0002 = 3,809 (A) If x is the
> A single card is drawn from a standard 52-card deck. Let D be the event that the card drawn is a diamond, and let F be the event that the card drawn is a face card. find the indicated probabilities. Answer:
> Refer to Problems 91 and 92. Write a brief verbal comparison of the two services described for customers who use a car for more than 10 hours in a month. A company sells custom embroidered apparel and promotional products. Table 1 shows the volume disco
> A car sharing service offers a membership plan with no monthly fee. Members who use a car for at most 10 hours are charged $15 per hour. Members who use a car for more than 10 hours are charged $10 per hour.
> Let Æ’ be defined by.
> Compute the following limit for each function in Problems.
> Compute the following limit for each function.
> Compute the following limit for each function.
> Compute the following limit for each function.
> Is the limit expression a 0>0 indeterminate form? Find the limit or explain why the limit does not exist.
> Is the limit expression a 0>0 indeterminate form? Find the limit or explain why the limit does not exist.
> Is the limit expression a 0>0 indeterminate form? Find the limit or explain why the limit does not exist.
> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of drawing 1 card from a standard 52-card deck , what is the probability of drawing. Figure 4: A six or club.
> Is the limit expression a 0>0 indeterminate form? Find the limit or explain why the limit does not exist.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> A single card is drawn from a standard 52-card deck. Let D be the event that the card drawn is a diamond, and let F be the event that the card drawn is a face card. find the indicated probabilities
> Find each indicated quantity if it exists.
> Find each indicated quantity if it exists.
> Sketch a possible graph of a function that satisfies the given conditions.
> Find the indicated limits.
> Find the indicated limits.
> Find the indicated limits.
> Find the indicated limits. Answer:
> Find each limit if it exists.
> Find each limit if it exists.
> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of drawing 1 card from a standard 52-card deck , what is the probability of drawing. Figure 4: A red queen.
> Find each limit if it exists.
> Find each limit if it exists.
> Find each limit if it exists.
> Use the graph of the function f shown to estimate the indicated limits and function values.
> Use the graph of the function f shown to estimate the indicated limits and function values.
> Use the graph of the function g shown to estimate the indicated limits and function values.
> Use the graph of the function g shown to estimate the indicated limits and function values.
> Use the graph of the function g shown to estimate the indicated limits and function values.
> Use the graph of the function g shown to estimate the indicated limits and function values.
> Use the graph of the function f shown to estimate the indicated limits and function values.
> A single card is drawn from a standard 52-card deck. Let D be the event that the card drawn is a diamond, and let F be the event that the card drawn is a face card. find the indicated probabilities.
> Write the expression as a quotient of integers, reduced to lowest terms.
> Use the graph of the function f shown to estimate the indicated limits and function values.
> Use the graph of the function f shown to estimate the indicated limits and function values.
> Use the graph of the function f shown to estimate the indicated limits and function values.
> You draw and keep a single bill from a hat that contains a $1, $10, $20, $50, and $100 bill. What is the expected value of the game to you?
> If the probability distribution for the random variable X is given in the table, what is the expected value of X?
> Find the average (mean) of the exam scores in Problem 2, if each score is divided by 2.
> Find the average (mean) of the exam scores in Problem 2, if 3 points are subtracted from each score.
> Find the average (mean) of the exam scores 78, 64, 97, 60, 86, and 83.
> Repeat Problem 55, assuming that the Grand Prize is currently $400,000,000. Data from Problem 55: A $2 Powerball lottery ticket has a 1/27.05 prob- 2. (A) ability of winning $4, a 1/317.39 probability of winning $7, a 1/10,376.47 probability of winning
> A pink-flowering plant is of genotype RW. If two such plants are crossed, we obtain a red plant (RR) with probability .25, a pink plant (RW or WR) with probability .50, and a white plant (WW) with probability .25, as shown in the table. What is the expec
> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of drawing 1 card from a standard 52-card deck , what is the probability of drawing. Figure 4: An ace.
> Repeat Problem 51, assuming that additional analysis caused the estimated probability of success in field B to be changed from .1 to .11. Data from Problem 51: After careful testing and analysis, an oil company is considering drilling in two different s
> An insurance company charges an annual premium of $75 for a $200,000 insurance policy against a house burning down. If the (empirical) probability that a house burns down in a given year is .0003, what is the expected value of the policy to the insurance
> A 3-card hand is dealt from a standard deck. You win $100 for each king in the hand. If the game is fair, how much should you lose if the hand contains no kings?
> Use a graphing calculator to simulate the results of placing a $1 bet on black in each of 400 games of roulette and compare the simulated and expected gains or losses.
> Repeat Problem 43 with the purchase of 10 tickets. Data from Problem 43: One thousand raffle tickets are sold at $1 each. Three tickets will be drawn at random (without replacement), and each will pay $200. Suppose you buy 5 tickets. (A) Create a payof
> A box of 8 flashbulbs contains 3 defective bulbs. A random sample of 2 is selected and tested. Let X be the random variable associated with the number of defective bulbs in a sample. (A) Find the probability distribution of X. (B) Find the expected num
> Ten thousand raffle tickets are sold at $2 each for a local library benefit. Prizes are awarded as follows: 2 prizes of $1,000, 4 prizes of $500, and 10 prizes of $100. What is the expected value of this raffle if you purchase 1 ticket?
> A game has an expected value to you of - $0.50. It costs $2 to play, but if you win, you receive $20 (including your $2 bet) for a net gain of $18. What is the probability of winning? Would you play this game? Discuss the factors that would influence you
> In roulette (see Problem 35), the numbers from 1 to 36 are evenly divided between red and black. A player who bets $1 on black wins $1 (and gets the $1 bet back) if the ball comes to rest on black; otherwise (if the ball lands on red, 0, or 00), the $1 b
> The payoff table for three possible courses of action is given below. Which of the three actions will produce the largest expected value? What is it?
> A single card is drawn from a standard 52-card deck. Let D be the event that the card drawn is a diamond, and let F be the event that the card drawn is a face card. find the indicated probabilities.
> A 5-card hand is dealt from a standard 52-card deck. If the hand contains at least one diamond, you win $10; otherwise, you lose $4. What is the expected value of the game?
> A card is drawn from a standard 52-card deck. If the card is a diamond, you win $10; otherwise, you lose $4. What is the expected value of the game?
> A coin is tossed three times. Suppose you lose $3 if 3 heads appear, lose $2 if 2 heads appear, and win $3 if 0 heads appear. How much should you win or lose if 1 head appears in order for the game to be fair?
> A single die is rolled once. You lose $12 if a number divisible by 3 turns up. How much should you win if a number not divisible by 3 turns up in order for the game to be fair? Describe the process and reasoning used to arrive at your answer.
> On three rolls of a single die, you will lose $10 if a 5 turns up at least once, and you will win $7 otherwise. What is the expected value of the game?
> In Problem 21, for the game to be fair, how much should you lose if a head and a tail turn up? Data from Problem 21: Two coins are flipped. You win $2 if either 2 heads or 2 tails turn up; you lose $3 if a head and a tail turn up. What is the expected v
> Repeat Problem 19 with the same game costing $3.50 for each play. Data from Problem 19: After paying $4 to play, a single fair die is rolled, and you are paid back the number of dollars corresponding to the number of dots facing up. For example, if a 5
> Repeat Problem 17, assuming an unfair coin with the probability of a head being .55 and a tail being .45 Data from Problem 17: A fair coin is flipped. If a head turns up, you win $1. If a tail turns up, you lose $1. What is the expected value of the gam
> In a family with 2 children, excluding multiple births and assuming that a boy is as likely as a girl at each birth, what is the expected number of boys?
> You draw a single card from a standard 52-card deck. If it is an ace, you win $104. Otherwise you get nothing. What is the expected value of the game to you?