Question: Solve the differential equation or initial-value
Solve the differential equation or initial-value problem using the method of undetermined coefficients.
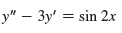
Transcribed Image Text:
y" – 3y' = sin 2x
> Solve the boundary-value problem, if possible. y'' + 16y = 0, y (0) = -3, y (π/8) = 2
> Assume that the earth is a solid sphere of uniform density with mass M and radius R = 3960 mi. For a particle of mass m within the earth at a distance r from the earth’s center, the gravitational force attracting the particle to the center is Fr = -GMr m
> Find a parametric representation for the surface. The part of the cylinder x2 + z2 = 9 that lies above the xy-plane and between the planes y = -4 and y = 4
> State Kepler’s Laws.
> Solve the differential equation using (a) undetermined coefficients and (b) variation of parameters. y" – y' = e*
> Solve the differential equation using (a) undetermined coefficients and (b) variation of parameters. y" – 2y' + y = e2x
> (a). Are the points P1 and P2 sources or sinks for the vector field F shown in the figure? Give an explanation based solely on the picture. (b). Given that F (x, y) = 〈x, y2〉, use the definition of divergence to verify
> If S is a sphere and F satisfies the hypotheses of Stokes’ Theorem, show that ∫∫S curl F ∙ dS = 0.
> The figure shows a pendulum with length L and the angle θ from the vertical to the pendulum. It can be shown that θ, as a function of time, satisfies the nonlinear differential equation where g is the acceleration due to gravi
> A particle moves along line segments from the origin to the points s1, 0, 0d, s1, 2, 1d, s0, 2, 1d, and back to the origin under the influence of the force field F (x, y, z) = z2 i + 2xy j + 4y2 k Find the work done.
> Graph the two basic solutions along with several other solutions of the differential equation. What features do the solutions have in common? d'y 2 dx? dy y= 0 %3D dx
> Graph the two basic solutions along with several other solutions of the differential equation. What features do the solutions have in common? d²y +2- dx? + 2y = 0 dx
> Discuss two applications of second-order linear differential equations.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. 1. If F is a vector field, then div F is a vector field. 2. If F is a vector field, then curl F is
> Graph the two basic solutions along with several other solutions of the differential equation. What features do the solutions have in common? d²y dy 4 4 + y = 0 dx? dx
> Verify that Stokes’ Theorem is true for the given vector field F and surface S. F (x, y, z) = 2y i + x j - 2 k, S is the cone z2 = x2 + y2, 0 < z < 4, oriented downward
> Graph the particular solution and several other solutions. What characteristics do these solutions have in common? y'' + 4y = e-x
> Show that if ω0 ≠ ω, but ω /ω 0 is a rational number, then the motion described by Equation 6 is periodic.
> As in Exercise 9, consider a spring with mass m, spring constant k, and damping constant c = 0, and let ω = √k/m. If an external force F (t) = F0 cos t is applied (the applied frequency equals the natural frequency), use the
> Suppose a spring has mass m and spring constant k and let ω = √k/m. Suppose that the damping constant is so small that the damping force is negligible. If an external force F (t) = F0 cos 0t is applied, where ω0 ≠ ω , use the method of undetermined coe
> A spring has a mass of 1 kg and its damping constant is c = 10. The spring starts from its equilibrium position with a velocity of 1 m/s. Graph the position function for the following values of the spring constant k: 10, 20, 25, 30, 40. What type of damp
> A spring has a mass of 1 kg and its spring constant is k = 100. The spring is released at a point 0.1 m above its equilibrium position. Graph the position function for the following values of the damping constant c: 10, 15, 20, 25, 30. What type of dampi
> Identify the surface with the given vector equation. r (s, t) =〈3 cos t, s, sin t〉, -1 < s < 1
> Use Stokes’ Theorem to evaluate ∫∫S curl F dS. F (x, y, z) = xyz i + xy j + x2yz k, S consists of the top and the four sides (but not the bottom) of the cube with vertices (±1, ±1, ±1), oriented outward
> Solve the differential equation. y'' - 2y' + 10y = 0
> Verify that the Divergence Theorem is true for the vector field F on the region E. F (x, y, z) = 〈x2, 2y, z〉, E is the solid cylinder y2 + z2 < 9, 0 < x < 2
> A spring with a mass of 2 kg has damping constant 14, and a force of 6 N is required to keep the spring stretched 0.5 m beyond its natural length. The spring is stretched 1 m beyond its natural length and then released with zero velocity. Find the positi
> Use power series to solve the differential equation. y' = xy
> A spring has natural length 0.75 m and a 5-kg mass. A force of 25 N is needed to keep the spring stretched to a length of 1 m. If the spring is stretched to a length of 1.1 m and then released with velocity 0, find the position of the mass after t second
> What are the traces of a surface? How do you find them?
> (a). How do you find the distance from a point to a line? (b). How do you find the distance from a point to a plane? (c). How do you find the distance between two lines?
> (a). Describe a method for determining whether three points P, Q, and R lie on the same line. (b). Describe a method for determining whether four points P, Q, R, and S lie in the same plane.
> (a). How do you tell if two vectors are parallel? (b). How do you tell if two vectors are perpendicular? (c). How do you tell if two planes are parallel?
> Write a vector equation and a scalar equation for a plane.
> Write a vector equation, parametric equations, and symmetric equations for a line.
> A vector field F, a curve C, and a point P are shown. (a). Is ∫C F dr positive, negative, or zero? Explain. (b). Is div F (P) positive, negative, or zero? Explain. P
> How do you find a vector perpendicular to a plane?
> How are cross products useful?
> How are dot products useful?
> If a is a vector and c is a scalar, how is ca related to a geometrically? How do you find ca algebraically?
> A spring with an 8-kg mass is kept stretched 0.4 m beyond its natural length by a force of 32 N. The spring starts at its equilibrium position and is given an initial velocity of 1 m/s. Find the position of the mass at any time t.
> Let F (x, y, z) = z tan-1 (y2) i + z3 ln (x2 + 1) j + z k. Find the flux of F across the part of the paraboloid x2 + y2 + z = 2 that lies above the plane z = 1 and is oriented upward.
> Graph the particular solution and several other solutions. What characteristics do these solutions have in common? y'' + 3y' + 2y = cos x
> Use Stokes’ Theorem to evaluate ∫C F ∙ dr. In each case C is oriented counterclockwise as viewed from above. F (x, y, z) = 2y i + xz j + (x + y) k, C is the curve of intersection of the plane z = y + 2 and the cylinder x2 + y2 = 1
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. у" — у' %3 хе", У(0) — 2, у(0) — 1
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. r(u, v) = (u, v², –v), -2 <u < 2, -2 < v< 2
> (a). What is an oriented surface? Give an example of a non-orientable surface. (b). Define the surface integral (or flux) of a vector field F over an oriented surface S with unit normal vector n. (c). How do you evaluate such an integral if S is a parame
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. у" — 2у + 5у %3Dsin x, y(0) 3D 1, у' (0) — 1
> Verify that the Divergence Theorem is true for the vector field F on the region E. F (x, y, z) = 〈z, y, x〉, E is the solid ball x2 + y2 + z2 < 16
> A hemisphere H and a portion P of a paraboloid are shown. Suppose F is a vector field on R3 whose components have continuous partial derivatives. Explain why [| curl F· dS || curl F ds H P P H
> Solve the initial-value problem. 4y'' - 20y' + 25y = 0, y (0) = 2, y' (0) = -3
> Solve the initial-value problem. y'' - 6y' + 10y = 0, y (0) = 2, y' (0) = 3
> (a). Use Stokes’ Theorem to evaluate ∫C F ∙ dr, where F (x, y, z) = x2y i + 1/3 x3 j + xy k and C is the curve of intersection of the hyperbolic paraboloid z = y2 - x2 and the cylinder x2 + y2 = 1, oriented counterclockwise as viewed from above. (b). Gr
> (a). Use Stokes’ Theorem to evaluate ∫C F ∙ dr, where F (x, y, z) = x2z i + xy2 j + z2 k and C is the curve of intersection of the plane x + y + z = 1 and the cylinder x2 + y2 = 9, oriented counterclockwise as viewed from above. (b). Graph both the plan
> Use Stokes’ Theorem to evaluate ∫C F ∙ dr. In each case C is oriented counterclockwise as viewed from above. F (x, y, z) = xy i + yz j + zx k, C is the boundary of the part of the paraboloid z = 1 - x2 - y2 in the first octant
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. r(и, в) — (и*, о?, и + »), -1 <u<1, - : 1 <v < 1
> (a). Write the definition of the surface integral of a scalar function f over a surface S. (b). How do you evaluate such an integral if S is a parametric surface given by a vector function r (u, v)? (c). What if S is given by an equation z = g (x, y)? (d
> Verify that the Divergence Theorem is true for the vector field F on the region E. F (x, y, z) = y2z3 i + 2yz j + 4z2 k, E is the solid enclosed by the paraboloid z = x2 + y2 and the plane z = 9
> Let F (x, y) = -y i + x j/ x2 + y2. (a). Show that ∂P/∂y = ∂Q/∂x. (b). Show that ∫C F ∙ dr is not independent of path. [Hint: Compute ∫C1 F ∙ dr and ∫C2 F ∙ dr, where C1 and C2 are the upper and lower halves of the circle x2 + y2 = 1 from (1, 0) to (-1,
> Determine whether or not the given set is (a) open, (b) connected, and (c) simply-connected. {(x, y) | (x, y) ≠ (2, 3)}
> Find an equation of the tangent plane to the given parametric surface at the specified point. х — и + 0, у %3 Зи*, г — и — 0; (2, 3, 0)
> A solid occupies a region E with surface S and is immersed in a liquid with constant density . We set up a coordinate system so that the xy-plane coincides with the surface of the liquid, and positive values of z are measured downward into the liquid. Th
> Evaluate the surface integral ∫∫S F ∙ dS for the given vector field F and the oriented surface S. In other words, find the flux of F across S. For closed surfaces, use the positive (outward) orientation. F (x, y, z) = x2 i + y2 j + z2 k, S is the bounda
> Use Exercise 29 to show that the line integral ∫C y dx + x dy + xyz dz is not independent of path. Exercise 29: Show that if the vector field F = P i + Q j + R k is conservative and P, Q, R have continuous first-order partial derivat
> Use a graphing device to produce a graph that looks like the given one. y
> Use a graphing device to produce a graph that looks like the given one. -3 -3 05 y
> Is the vector field shown in the figure conservative? Explain. y.
> (a). What is an initial-value problem for a second-order differential equation? (b). What is a boundary-value problem for such an equation?
> Find a parametric representation for the surface. The part of the ellipsoid x2 + 2y2 + 3z2 = 1 that lies to the left of the xz-plane
> Plot the vector field and guess where div F > 0 and where div F F(x, y) = (xy, x + y²)
> Let C be a simple closed smooth curve that lies in the plane x 1 y + z = 1. Show that the line integral ∫C z dx - 2x dy + 3ydz depends only on the area of the region enclosed by C and not on the shape of C or its location in the plane.
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. r(u, v) = (u³ – u) i + v² j + u
> Verify that Stokes’ Theorem is true for the given vector field F and surface S. F (x, y, z) = -2yz i + y j + 3x k, S is the part of the paraboloid z = 5 - x2 - y2 that lies above the plane z = 1, oriented upward
> Evaluate the surface integral ∫∫S F ∙ dS for the given vector field F and the oriented surface S. In other words, find the flux of F across S. For closed surfaces, use the positive (outward) orientation. F (x, y, z) = y i + (z – y) j + x k, S is the sur
> (a). If C is the line segment connecting the point (x1, y1) to the point (x2, y2), show that (b). If the vertices of a polygon, in counterclockwise order, are (x1, y1), (x2, y2), . . . , (xn , yn), show that the area of the polygon is (c). Find the a
> Evaluate the surface integral. ∫∫S (x2 + y2 + z2) dS, S is the part of the cylinder x2 + y2 = 9 between the planes z = 0 and z = 2, together with its top and bottom disks
> Evaluate ∫C (y + sin x) dx + (z2 + cos y) dy + x3 dz where C is the curve r (t) =〈sin t, cos t, sin 2t〉, 0 < t < 2π . [Hint: Observe that C lies on the surface z = 2xy.]
> Identify the surface with the given vector equation. r (u, v) = u2 i + u cos v j + u sin v k
> Show that F is conservative and use this fact to evaluate ∫C F ∙ dr along the given curve. F(x, y, z) = e'i + (xe' + e*)j + ye k, Cis the line segment from (0, 2, 0) to (4, 0, 3)
> Let H be the hemisphere x2 + y2 + z2 = 50, z > 0, and suppose f is a continuous function with f (3, 4, 5) = 7, f (3, -4, 5) = 8, f -3, 4, 5) = 9, and f (-3, -4, 5) = 12. By dividing H into four patches, estimate the value of ∫∫H f (x, y, z) dS.
> Use Stokes’ Theorem to evaluate ∫∫S curl F dS. F (x, y, z) = x2 sin z i + y2 j + xy k, S is the part of the paraboloid z = 1 - x2 - y2 that lies above the xy-plane, oriented upward
> Use one of the formulas in (5) to find the area under one arch of the cycloid x = t2 sin t, y = 1 - cos t.
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. x = sin u, y = cos u sin v, z=
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. х— cos'и сos'p, у%3 sin'u cos',
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. х%3 (1 — и)(3 + соs D) cos 4ти,
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. r(u, ») — ир?і + и?o ј + (u? —
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. r(u, v) = u cos vi + u sin vj +
> Use a computer to graph the parametric surface. Get a printout and indicate on its which grid curves have u constant and which have v constant. x = cos u, y = sin u sin v, z= cos v, 0 <u< 27, 0<v< 27
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. x = sin v, y = cos u sin 4v, z = sin 2u sin 4v, 0 <u< 2m, -T/2 < v< T/2
> Show that F is conservative and use this fact to evaluate ∫C F ∙ dr along the given curve. F(x, y) = (4x³y² – 2xy) i + (2x*y – 3x²y² + 4y®)j. C: r(t) = (t + sin mt) i + (2t + cos Tt)j, 0 < t< 1
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. r(u, v) = (u, sin(u+ v), sin v), -T <uE T, -T <V <T
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. r(и, v) — (и*, и sin v, и cos v), -1 <u < 1, 0 <o< 27
> Identify the surface with the given vector equation. r (s, t) = 〈s cos t, s sin t, s〉
> A surface S consists of the cylinder x2 + y2 = 1, -1 Estimate the value of ∫∫S f (x, y, z) dS by using a Riemann sum, taking the patches Sij to be four quarter-cylinders and the top and bottom disks. f(±1, 0, 0
> Let S be the surface of the box enclosed by the planes x = ±1, y = ±1, z = ±1. Approximate ∫∫S cos (x + 2y + 3z) dS by using a Riemann sum as in Definition 1, taking the patches Sij to be the squares that are the faces of the box S and the points P*ij to
> Maxwell’s equations relating the electric field E and magnetic field H as they vary with time in a region containing no charge and no current can be stated as follows: where c is the speed of light. Use these equations to prove the fo
> Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. Figure 9: F (x, y, z) = -y i ZA
> Determine whether or not the given set is (a) open, (b) connected, and (c) simply-connected. {(x, y) | 1 < |x | < 2}
> (a). What happens to the spiral tube in Example 2 (see Figure 5) if we replace cos u by sin u and sin u by cos u? (b). What happens if we replace cos u by cos 2u and sin u by sin 2u?
> Show that F is a conservative vector field. Then find a function f such that F = ∇f. F(x, y, z) = sin yi + x cos yj – sin z k

