Question: Plot the vector field and guess where
Plot the vector field and guess where div F > 0 and where div F
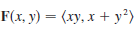
Transcribed Image Text:
F(x, y) = (xy, x + y²)
> A spring has a mass of 1 kg and its spring constant is k = 100. The spring is released at a point 0.1 m above its equilibrium position. Graph the position function for the following values of the damping constant c: 10, 15, 20, 25, 30. What type of dampi
> Identify the surface with the given vector equation. r (s, t) =〈3 cos t, s, sin t〉, -1 < s < 1
> Use Stokes’ Theorem to evaluate ∫∫S curl F dS. F (x, y, z) = xyz i + xy j + x2yz k, S consists of the top and the four sides (but not the bottom) of the cube with vertices (±1, ±1, ±1), oriented outward
> Solve the differential equation. y'' - 2y' + 10y = 0
> Verify that the Divergence Theorem is true for the vector field F on the region E. F (x, y, z) = 〈x2, 2y, z〉, E is the solid cylinder y2 + z2 < 9, 0 < x < 2
> A spring with a mass of 2 kg has damping constant 14, and a force of 6 N is required to keep the spring stretched 0.5 m beyond its natural length. The spring is stretched 1 m beyond its natural length and then released with zero velocity. Find the positi
> Use power series to solve the differential equation. y' = xy
> A spring has natural length 0.75 m and a 5-kg mass. A force of 25 N is needed to keep the spring stretched to a length of 1 m. If the spring is stretched to a length of 1.1 m and then released with velocity 0, find the position of the mass after t second
> What are the traces of a surface? How do you find them?
> (a). How do you find the distance from a point to a line? (b). How do you find the distance from a point to a plane? (c). How do you find the distance between two lines?
> (a). Describe a method for determining whether three points P, Q, and R lie on the same line. (b). Describe a method for determining whether four points P, Q, R, and S lie in the same plane.
> (a). How do you tell if two vectors are parallel? (b). How do you tell if two vectors are perpendicular? (c). How do you tell if two planes are parallel?
> Write a vector equation and a scalar equation for a plane.
> Write a vector equation, parametric equations, and symmetric equations for a line.
> A vector field F, a curve C, and a point P are shown. (a). Is ∫C F dr positive, negative, or zero? Explain. (b). Is div F (P) positive, negative, or zero? Explain. P
> How do you find a vector perpendicular to a plane?
> How are cross products useful?
> How are dot products useful?
> If a is a vector and c is a scalar, how is ca related to a geometrically? How do you find ca algebraically?
> A spring with an 8-kg mass is kept stretched 0.4 m beyond its natural length by a force of 32 N. The spring starts at its equilibrium position and is given an initial velocity of 1 m/s. Find the position of the mass at any time t.
> Let F (x, y, z) = z tan-1 (y2) i + z3 ln (x2 + 1) j + z k. Find the flux of F across the part of the paraboloid x2 + y2 + z = 2 that lies above the plane z = 1 and is oriented upward.
> Graph the particular solution and several other solutions. What characteristics do these solutions have in common? y'' + 3y' + 2y = cos x
> Use Stokes’ Theorem to evaluate ∫C F ∙ dr. In each case C is oriented counterclockwise as viewed from above. F (x, y, z) = 2y i + xz j + (x + y) k, C is the curve of intersection of the plane z = y + 2 and the cylinder x2 + y2 = 1
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. у" — у' %3 хе", У(0) — 2, у(0) — 1
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. r(u, v) = (u, v², –v), -2 <u < 2, -2 < v< 2
> (a). What is an oriented surface? Give an example of a non-orientable surface. (b). Define the surface integral (or flux) of a vector field F over an oriented surface S with unit normal vector n. (c). How do you evaluate such an integral if S is a parame
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. у" — 2у + 5у %3Dsin x, y(0) 3D 1, у' (0) — 1
> Verify that the Divergence Theorem is true for the vector field F on the region E. F (x, y, z) = 〈z, y, x〉, E is the solid ball x2 + y2 + z2 < 16
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. y" – 3y' = sin 2x
> A hemisphere H and a portion P of a paraboloid are shown. Suppose F is a vector field on R3 whose components have continuous partial derivatives. Explain why [| curl F· dS || curl F ds H P P H
> Solve the initial-value problem. 4y'' - 20y' + 25y = 0, y (0) = 2, y' (0) = -3
> Solve the initial-value problem. y'' - 6y' + 10y = 0, y (0) = 2, y' (0) = 3
> (a). Use Stokes’ Theorem to evaluate ∫C F ∙ dr, where F (x, y, z) = x2y i + 1/3 x3 j + xy k and C is the curve of intersection of the hyperbolic paraboloid z = y2 - x2 and the cylinder x2 + y2 = 1, oriented counterclockwise as viewed from above. (b). Gr
> (a). Use Stokes’ Theorem to evaluate ∫C F ∙ dr, where F (x, y, z) = x2z i + xy2 j + z2 k and C is the curve of intersection of the plane x + y + z = 1 and the cylinder x2 + y2 = 9, oriented counterclockwise as viewed from above. (b). Graph both the plan
> Use Stokes’ Theorem to evaluate ∫C F ∙ dr. In each case C is oriented counterclockwise as viewed from above. F (x, y, z) = xy i + yz j + zx k, C is the boundary of the part of the paraboloid z = 1 - x2 - y2 in the first octant
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. r(и, в) — (и*, о?, и + »), -1 <u<1, - : 1 <v < 1
> (a). Write the definition of the surface integral of a scalar function f over a surface S. (b). How do you evaluate such an integral if S is a parametric surface given by a vector function r (u, v)? (c). What if S is given by an equation z = g (x, y)? (d
> Verify that the Divergence Theorem is true for the vector field F on the region E. F (x, y, z) = y2z3 i + 2yz j + 4z2 k, E is the solid enclosed by the paraboloid z = x2 + y2 and the plane z = 9
> Let F (x, y) = -y i + x j/ x2 + y2. (a). Show that ∂P/∂y = ∂Q/∂x. (b). Show that ∫C F ∙ dr is not independent of path. [Hint: Compute ∫C1 F ∙ dr and ∫C2 F ∙ dr, where C1 and C2 are the upper and lower halves of the circle x2 + y2 = 1 from (1, 0) to (-1,
> Determine whether or not the given set is (a) open, (b) connected, and (c) simply-connected. {(x, y) | (x, y) ≠ (2, 3)}
> Find an equation of the tangent plane to the given parametric surface at the specified point. х — и + 0, у %3 Зи*, г — и — 0; (2, 3, 0)
> A solid occupies a region E with surface S and is immersed in a liquid with constant density . We set up a coordinate system so that the xy-plane coincides with the surface of the liquid, and positive values of z are measured downward into the liquid. Th
> Evaluate the surface integral ∫∫S F ∙ dS for the given vector field F and the oriented surface S. In other words, find the flux of F across S. For closed surfaces, use the positive (outward) orientation. F (x, y, z) = x2 i + y2 j + z2 k, S is the bounda
> Use Exercise 29 to show that the line integral ∫C y dx + x dy + xyz dz is not independent of path. Exercise 29: Show that if the vector field F = P i + Q j + R k is conservative and P, Q, R have continuous first-order partial derivat
> Use a graphing device to produce a graph that looks like the given one. y
> Use a graphing device to produce a graph that looks like the given one. -3 -3 05 y
> Is the vector field shown in the figure conservative? Explain. y.
> (a). What is an initial-value problem for a second-order differential equation? (b). What is a boundary-value problem for such an equation?
> Find a parametric representation for the surface. The part of the ellipsoid x2 + 2y2 + 3z2 = 1 that lies to the left of the xz-plane
> Let C be a simple closed smooth curve that lies in the plane x 1 y + z = 1. Show that the line integral ∫C z dx - 2x dy + 3ydz depends only on the area of the region enclosed by C and not on the shape of C or its location in the plane.
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. r(u, v) = (u³ – u) i + v² j + u
> Verify that Stokes’ Theorem is true for the given vector field F and surface S. F (x, y, z) = -2yz i + y j + 3x k, S is the part of the paraboloid z = 5 - x2 - y2 that lies above the plane z = 1, oriented upward
> Evaluate the surface integral ∫∫S F ∙ dS for the given vector field F and the oriented surface S. In other words, find the flux of F across S. For closed surfaces, use the positive (outward) orientation. F (x, y, z) = y i + (z – y) j + x k, S is the sur
> (a). If C is the line segment connecting the point (x1, y1) to the point (x2, y2), show that (b). If the vertices of a polygon, in counterclockwise order, are (x1, y1), (x2, y2), . . . , (xn , yn), show that the area of the polygon is (c). Find the a
> Evaluate the surface integral. ∫∫S (x2 + y2 + z2) dS, S is the part of the cylinder x2 + y2 = 9 between the planes z = 0 and z = 2, together with its top and bottom disks
> Evaluate ∫C (y + sin x) dx + (z2 + cos y) dy + x3 dz where C is the curve r (t) =〈sin t, cos t, sin 2t〉, 0 < t < 2π . [Hint: Observe that C lies on the surface z = 2xy.]
> Identify the surface with the given vector equation. r (u, v) = u2 i + u cos v j + u sin v k
> Show that F is conservative and use this fact to evaluate ∫C F ∙ dr along the given curve. F(x, y, z) = e'i + (xe' + e*)j + ye k, Cis the line segment from (0, 2, 0) to (4, 0, 3)
> Let H be the hemisphere x2 + y2 + z2 = 50, z > 0, and suppose f is a continuous function with f (3, 4, 5) = 7, f (3, -4, 5) = 8, f -3, 4, 5) = 9, and f (-3, -4, 5) = 12. By dividing H into four patches, estimate the value of ∫∫H f (x, y, z) dS.
> Use Stokes’ Theorem to evaluate ∫∫S curl F dS. F (x, y, z) = x2 sin z i + y2 j + xy k, S is the part of the paraboloid z = 1 - x2 - y2 that lies above the xy-plane, oriented upward
> Use one of the formulas in (5) to find the area under one arch of the cycloid x = t2 sin t, y = 1 - cos t.
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. x = sin u, y = cos u sin v, z=
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. х— cos'и сos'p, у%3 sin'u cos',
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. х%3 (1 — и)(3 + соs D) cos 4ти,
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. r(u, ») — ир?і + и?o ј + (u? —
> Match the equations with the graphs labeled I–VI and give reasons for your answers. Determine which families of grid curves have u constant and which have v constant. I II ZA III IV ZA ZA V ZA VI z. r(u, v) = u cos vi + u sin vj +
> Use a computer to graph the parametric surface. Get a printout and indicate on its which grid curves have u constant and which have v constant. x = cos u, y = sin u sin v, z= cos v, 0 <u< 27, 0<v< 27
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. x = sin v, y = cos u sin 4v, z = sin 2u sin 4v, 0 <u< 2m, -T/2 < v< T/2
> Show that F is conservative and use this fact to evaluate ∫C F ∙ dr along the given curve. F(x, y) = (4x³y² – 2xy) i + (2x*y – 3x²y² + 4y®)j. C: r(t) = (t + sin mt) i + (2t + cos Tt)j, 0 < t< 1
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. r(u, v) = (u, sin(u+ v), sin v), -T <uE T, -T <V <T
> Use a computer to graph the parametric surface. Get a printout and indicate on it which grid curves have u constant and which have v constant. r(и, v) — (и*, и sin v, и cos v), -1 <u < 1, 0 <o< 27
> Identify the surface with the given vector equation. r (s, t) = 〈s cos t, s sin t, s〉
> A surface S consists of the cylinder x2 + y2 = 1, -1 Estimate the value of ∫∫S f (x, y, z) dS by using a Riemann sum, taking the patches Sij to be four quarter-cylinders and the top and bottom disks. f(±1, 0, 0
> Let S be the surface of the box enclosed by the planes x = ±1, y = ±1, z = ±1. Approximate ∫∫S cos (x + 2y + 3z) dS by using a Riemann sum as in Definition 1, taking the patches Sij to be the squares that are the faces of the box S and the points P*ij to
> Maxwell’s equations relating the electric field E and magnetic field H as they vary with time in a region containing no charge and no current can be stated as follows: where c is the speed of light. Use these equations to prove the fo
> Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. Figure 9: F (x, y, z) = -y i ZA
> Determine whether or not the given set is (a) open, (b) connected, and (c) simply-connected. {(x, y) | 1 < |x | < 2}
> (a). What happens to the spiral tube in Example 2 (see Figure 5) if we replace cos u by sin u and sin u by cos u? (b). What happens if we replace cos u by cos 2u and sin u by sin 2u?
> Show that F is a conservative vector field. Then find a function f such that F = ∇f. F(x, y, z) = sin yi + x cos yj – sin z k
> Show that the line integral is independent of path and evaluate the integral. ∫C sin y dx + (x cos y - sin y) dy, C is any path from (2, 0) to (1, π)
> Identify the surface with the given vector equation. r (u, v) = (u + v) i + (3 – v) j + (1 + 4u + 5v) k
> Determine whether the points P and Q lie on the given surface. r (u, v) = 〈1 + u - v, u + v2, u2 - v2〉 P (1, 2, 1), Q (2, 3, 3)
> Determine whether the points P and Q lie on the given surface. r (u, v) = 〈u + v, u - 2v, 3 + u – v〉 P (4, -5, 1), Q (0, 4, 6)
> A particle moves in a velocity field V (x, y) = 〈x^2, x, + y^2 〉 If it is at position s2, 1d at time t − 3, estimate its location at time t = 3.01.
> If you have a CAS that plots vector fields (the command is field plot in Maple and Plot Vector Field or Vector Plot in Mathematica), use it to plot F (x, y) = (y2 - 2xy) i +) (3xy - 6x2) j Explain the appearance by finding the set of points (x, y) such t
> Match the functions f with the plots of their gradient vector fields labeled I–IV. Give reasons for your choices. f (x, y) = (x + y)2 II 4 -4 4 -4
> Plot the gradient vector field of f together with a contour map of f. Explain how they are related to each other. f (x, y) = cos x - 2 sin y
> Match the vector fields F on R3 with the plots labeled I–IV. Give reasons for your choices. F (x, y, z) = x i + y j + z k IV z 0 z 0- -10 y 10-1
> (a). What is a function of two variables? (b). Describe three methods for visualizing a function of two variables.
> (a). What is a parametric surface? What are its grid curves? (b). Write an expression for the area of a parametric surface. (c). What is the area of a surface given by an equation z = t (x, y)?
> (a). Find the work done by the force field F (x, y) = x2 i + xy j on a particle that moves once around the circle x2 + y2 = 4 oriented in the counterclockwise direction. (b). Use a computer algebra system to graph the force field and circle on the same s
> (a). Evaluate the line integral ∫C F ∙ dr, where F (x, y) = ex-1 i + xy j and C is given by r(t) = t2 i + t3 j, 0 (b). Illustrate part (a) by using a graphing calculator or computer to graph C and the vectors from the
> Determine whether or not the given set is (a) open, (b) connected, and (c) simply-connected. {(x, y) | 1 < x2 + y2 < 4, y > 0}
> Use Green’s Theorem to prove the change of variables formula for a double integral (Formula 15.9.9) for the case where f (x, y) = 1: Here R is the region in the xy-plane that corresponds to the region S in the uv-plane under the trans
> Let F = ∇f, where f (x, y) = sin (x - 2y). Find curves C1 and C2 that are not closed and satisfy the equation. (a) f. F· dr = 0 JCI (b) f. (b) F. dr = 1
> Use the method of Example 5 to calculate ∫C F ∙ dr, where and C is any positively oriented simple closed curve that encloses the origin. F(x, y) = 2хyi + (у? — х?)j (x? + у?)?
> Is the vector field shown in the figure conservative? Explain.
> Match the vector fields F with the plots labeled I–IV. Give reasons for your choices. F (x, y) = 〈x, -y〉 I 3 -3 3 -3
> (a). How do you find the velocity, speed, and acceleration of a particle that moves along a space curve? (b). Write the acceleration in terms of its tangential and normal components.
> Determine whether or not the vector field is conservative. If it is conservative, find a function f such that F = ∇f. F (x, y, z) = ex sin yz i + zex cos yz j + yex cos yz k

