Question: Summarize the pertinent information obtained by
Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
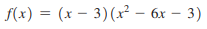
> Note that L’Hôpital’s rule does not apply to every problem, and some problems will require more than one application of L’Hôpital’s rule.
> Note that L’Hôpital’s rule does not apply to every problem, and some problems will require more than one application of L’Hôpital’s rule.
> Note that L’Hôpital’s rule does not apply to every problem, and some problems will require more than one application of L’Hôpital’s rule.
> Note that L’Hôpital’s rule does not apply to every problem, and some problems will require more than one application of L’Hôpital’s rule.
> Note that L’Hôpital’s rule does not apply to every problem, and some problems will require more than one application of L’Hôpital’s rule.
> Note that L’Hôpital’s rule does not apply to every problem, and some problems will require more than one application of L’Hôpital’s rule.
> explain why L’Hôpital’s rule does not apply. If the limit exists, find it by other means.
> explain why L’Hôpital’s rule does not apply. If the limit exists, find it by other means.
> Use L’Hôpital’s rule to find the limit. Note that in these problems, neither algebraic simplification nor Theorem 4 of Section 9.2 provides an alternative to L’Hôpital&acir
> To test a new car, an automobile manufacturer wants to select 4 employees to test-drive the car for 1 year. If 12 management and 8 union employees volunteer to be test drivers and the selection is made at random, what is the probability that at least 1 u
> Use L’Hôpital’s rule to find the limit. Note that in these problems, neither algebraic simplification nor Theorem 4 of Section 9.2 provides an alternative to L’Hôpital&acir
> Use L’Hôpital’s rule to find the limit. Note that in these problems, neither algebraic simplification nor Theorem 4 of Section 9.2 provides an alternative to L’Hôpital&acir
> Use L’Hôpital’s rule to find the limit. Note that in these problems, neither algebraic simplification nor Theorem 4 of Section 9.2 provides an alternative to L’Hôpital&acir
> even though the limit can be found using Theorem 4 of Section 9.2, use L’Hôpital’s rule to find the limit.
> even though the limit can be found using Theorem 4 of Section 9.2, use L’Hôpital’s rule to find the limit.
> even though the limit can be found using Theorem 4 of Section 9.2, use L’Hôpital’s rule to find the limit.
> even though the limit can be found using Theorem 4 of Section 9.2, use L’Hôpital’s rule to find the limit.
> even though the limit can be found using algebraic simplification as in Section 9.1, use L’Hôpital’s rule to find the limit.
> even though the limit can be found using algebraic simplification as in Section 9.1, use L’Hôpital’s rule to find the limit.
> Use the graph of y = g(x), assuming g″(x) > 0 if x = c or g, to identify (A) Intervals on which the graph of g is concave upward (B) Intervals on which the graph of g is concave downward (C) Intervals on which g″
> Find the probability of being dealt the given hand from a standard 52-card deck. Refer to the description of a standard 52-card deck on page 384. A 7-card hand that contains exactly 1 king and exactly 2 jacks.
> inspect the graph of the function to determine whether it is concave up, concave down, or neither, on the given interval.
> inspect the graph of the function to determine whether it is concave up, concave down, or neither, on the given interval.
> inspect the graph of the function to determine whether it is concave up, concave down, or neither, on the given interval.
> inspect the graph of the function to determine whether it is concave up, concave down, or neither, on the given interval. The identity function, (x) = x, on ( - ∞, ∞)
> One hour after x milligrams of a particular drug are given to a person, the change in body temperature T(x), in degrees Fahrenheit, is given by The rate T′1x2 at which T1x2 changes with respect to the size of the dosage x is called the
> A sporting goods chain places TV ad to promote golf club sales. The marketing director used past records to determine the following data, where x is the number of ads placed monthly and y is the number of golf clubs sold that month. (A) Enter the data
> A company estimates that it will sell N1x2 units of a product after spending $x thousand on advertising, as given by N(x) = -0.5x4 + 26x3 - 360x2 + 20,000 15 ≤ x ≤ 24 When is the rate of change of sales increasing and when is it decreasing? What is th
> A baseball cap manufacturer is planning to expand its workforce. It estimates that the number of baseball caps produced by hiring x new workers is given by T(x) = -0.25x4 + 6x3 0 ≤ x ≤ 18 When is the rate of change of baseball cap production increasin
> A national food service runs food concessions for sporting events throughout the country. The company’s marketing research department chose a particular football stadium to test market a new jumbo hot dog. It was found that the demand for the new hot dog
> Suppose that the cost equation for a company is C(x) = 830 + 396x (A) Find the local extrema for the profit function. (B) On which intervals is the graph of the profit function concave upward? Concave downward?
> An assembly plant produces 40 outboard motors, including 7 that are defective. The quality control department selects 10 at random (from the 40 produced) for testing and will shut down the plant for troubleshooting if 1 or more in the sample are found to
> The company in Problem 85 produces the same camp stove at another plant. The total cost C(x) (in dollars) of producing x camp stoves per week at plant B is shown in the figure. Discuss the graph of the marginal cost function C′(x) and
> Another commonly used measure of inflation is the annual rate of change of the Producer Price Index (PPI). A government report states that the annual rate of change of the PPI is decreasing. What does this say about the shape of the graph of the PPI?
> apply steps 1–3 of the graphing strategy to (x). Use a graphing calculator to approximate (to two decimal places) x intercepts, critical numbers, and inflection points. Summarize all the pertinent information.
> apply steps 1–3 of the graphing strategy to (x). Use a graphing calculator to approximate (to two decimal places) x intercepts, critical numbers, and inflection points. Summarize all the pertinent information.
> use the graph of y = ′(x) to discuss the graph of y = (x). Organize your conclusions in a table, and sketch a possible graph of y = (x).
> use the graph of y = ′(x) to discuss the graph of y = (x). Organize your conclusions in a table, and sketch a possible graph of y = (x).
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> Find the probability of being dealt the given hand from a standard 52-card deck. Refer to the description of a standard 52-card deck on page 384. A 4-card hand that contains no face cards.
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y = (x).
> (x) is continuous on (- ∞, ∞). Use the given information to sketch the graph of .
> (x) is continuous on (- ∞, ∞). Use the given information to sketch the graph of .
> (x) is continuous on (- ∞, ∞). Use the given information to sketch the graph of .
> Use the (empirical) probabilities in Problem 81 to find the probability that a city driver selected at random (A) Drives more than 15,000 miles per year or has an accident (B) Drives 15,000 or fewer miles per year and has an accident. Data from problem
> (x) is continuous on (- ∞, ∞). Use the given information to sketch the graph of .
> use the given sign chart to sketch a possible graph of .
> use the given sign chart to sketch a possible graph of .
> Find the intervals on which the graph of  is concave upward, the intervals on which the graph of  is concave downward, and the x, y coordinates of the inflection points.
> Find the intervals on which the graph of  is concave upward, the intervals on which the graph of  is concave downward, and the x, y coordinates of the inflection points.
> Find the intervals on which the graph of  is concave upward, the intervals on which the graph of  is concave downward, and the x, y coordinates of the inflection points.
> Find the intervals on which the graph of  is concave upward, the intervals on which the graph of  is concave downward, and the x, y coordinates of the inflection points.
> Find the intervals on which the graph of  is concave upward, the intervals on which the graph of  is concave downward, and the x, y coordinates of the inflection points.
> find the x and y coordinates of all inflection points.
> find the x and y coordinates of all inflection points.
> Find the probability of being dealt the given hand from a standard 52-card deck. Refer to the description of a standard 52-card deck on page 384. A 6-card hand that contains exactly two clubs.
> find the x and y coordinates of all inflection points.
> find the indicated derivative for each function.
> find the indicated derivative for each function.
> find the indicated derivative for each function.
> find the indicated derivative for each function.
> match the indicated conditions with one of the graphs (A)–(D) shown in the figure.
> match the indicated conditions with one of the graphs (A)–(D) shown in the figure.
> Use the graph of y = (x) to identify (A) The local extrema of (x). (B) The inflection points of (x). (C) The numbers u for which ′(u)is a local extremum of ′(x).
> (x) is continuous on 1 - ∞, ∞2 and has critical numbers at x = a, b, c, and d. Use the sign chart for ′ (x) to determine whether f has a local maximum, a local
> Refer to the following graph of y = (x): Identify the x coordinates of the points where (x has a local minimum.
> Refer to Problem 79. If a university student is selected at random, what is the (empirical) probability that (A) The student does not own a car? (B) The student owns a car but not a laptop. Data from problem 79: From a survey involving 1,000 university
> Refer to the Venn diagram below for events A and B in an equally likely sample space S. Find each of the indicated probabilities.
> Refer to the following graph of y = (x): Identify the x coordinates of the points where ′(x) does not exist.
> Refer to the following graph of y = (x): Identify the intervals on which ′ (x) > 0.
> Refer to the following graph of y = (x): Identify the intervals on which f1x2 is decreasing
> inspect the graph of the function to determine whether it is increasing or decreasing on the given interval.
> inspect the graph of the function to determine whether it is increasing or decreasing on the given interval.
> inspect the graph of the function to determine whether it is increasing or decreasing on the given interval.
> inspect the graph of the function to determine whether it is increasing or decreasing on the given interval.
> The concentration C(t), in milligrams per cubic centimeter, of a particular drug in a patient’s bloodstream is given by where t is the number of hours after the drug is taken orally. Find the critical numbers of C(t), the intervals on
> A manufacturer incurs the following costs in producing x rain jackets in one day for 0 6 x 6 200: fixed costs, $450; unit production cost, $30 per jacket; equipment maintenance and repairs, 0.08x2 dollars. (A) What is the average cost C(x) per jacket if
> The figure approximates the rate of change of the price of eggs over a 70-month period, where E1t2 is the price of a dozen eggs (in dollars) and t is time (in months). (A) Write a brief description of the graph of y = E(t), including a discussion of any
> Find the probability of being dealt the given hand from a standard 52-card deck. Refer to the description of a standard 52-card deck on page 384. A 5-card hand that consists entirely of face cards.
> The graph of the total revenue R(x) (in dollars) from the sale of x cordless electric screwdrivers is shown in the figure. (A) Write a brief description of the graph of the marginal revenue function y = R′(x), including a discussion o
> Find the critical numbers, the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema. Do not graph
> Find the critical numbers, the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema. Do not graph
> Find the critical numbers, the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema. Do not graph
> use the given graph of y = (x) to find the intervals on which ′(x) > 0, the intervals on which ′(x) 6 0, and the values of x for which 
> use the given graph of y = (x) to find the intervals on which ′(x) > 0, the intervals on which ′(x) 6 0, and the values of x for which 
> use the given graph of y = ′(x) to find the intervals on which  is increasing, the intervals on which  is decreasing, and the x coordinates of the local extrema of ï‚
> use the given graph of y = ′(x) to find the intervals on which  is increasing, the intervals on which  is decreasing, and the x coordinates of the local extrema of ï‚
> use the given graph of y = ′(x) to find the intervals on which  is increasing, the intervals on which  is decreasing, and the x coordinates of the local extrema of ï‚
> involve functions 1-6 and their derivatives, g1-g6. Use the graphs shown in figures (A) and (B) to match each function fi with its derivative gj . 
> Consider the command in Figure A and the associated statistical plot in Figure B. (A) Explain why the command does not simulate 50 repetitions of rolling a pair of dice and recording their sum. (B) Describe an experiment that is simulated by this comma
> involve functions 1-6 and their derivatives, g1-g6. Use the graphs shown in figures (A) and (B) to match each function fi with its derivative gj . 
> involve functions 1-6 and their derivatives, g1-g6. Use the graphs shown in figures (A) and (B) to match each function fi with its derivative gj . 

